今回は数独(ナンプレ)をプログラミングで解く方法の解説と、バックトラック法で数独を解くサンプルプログラムの紹介をしたいと思います。
Contents
数独(ナンプレ)とは
まずは数独(ナンプレ)について理解しましょう。
どんなゲームでも、特にプログラミングでそのゲームを解くためにはルールをしっかり理解することが重要です!
数独は下図のように 9×9 のマスに対し、空いてるマスに数字を入れていくゲームになります(数字の配置は Wikipedia に載せられているものを使用させていただいています)。
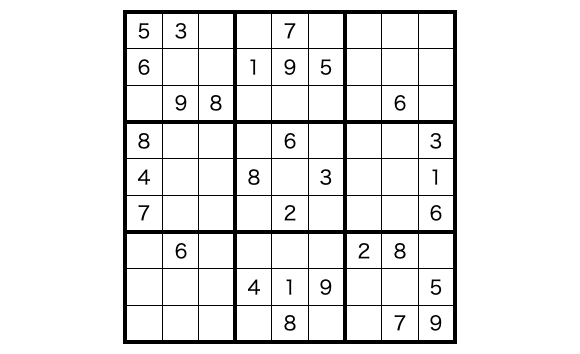
具体的な遊び方は下記のようになります。
- 入れる数字は 1 〜 9 の 9 種類
- 同じ列・同じ行・同じブロック内(太線の正方形内)に同じ数字を入れてはダメ
- 上記を満たして全てのマスを埋めることができればゲームクリア
ゲームクリア時は下の図のように各行・各列・各ブロックには 1 〜 9 の数字が 1 つずつ入っていることになります。
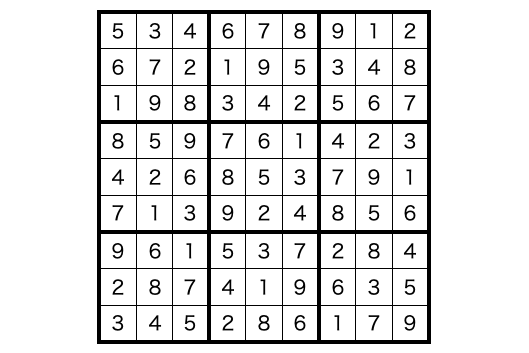
このようにゲームクリア時の数字の配置パターンを、その問題に対する「解」と呼びます。
今回紹介した最初の数字の配置だと解は1つのみですが、最初の数字の配置によっては解が複数の場合もあります。
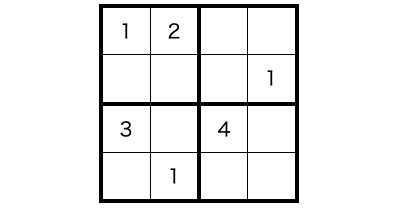
また、ここまで 9×9 のマス数限定で話をしてきましたが他のサイズの数独問題もあります。例えば 4×4 のマスの数独もあります。この場合、入れる数字は 1 〜 4 の 4 種類の数字になります。
数独をプログラミングで解く方法
続いて数独をプログラミングで解く方法について解説していきます。
スポンサーリンク
全てのパターンを総当たりで解く
一つ目の方法は「全てのパターンを総当たりで解く」です。
基本的に数独のような「解となり得るパターンを見つけ出すゲーム」に関しては、全てのパターンに対して「解として成立しているか」を調べてやれば、いつかは必ず解を見つけ出すことができます。
数独の場合は「数字の配置」の全パターンに対し、下記を満たしているか(解として成立しているか)を調べてやれば良いということになります(ただし最初から数字が配置されている場合は、その数字は固定して調べます)。
- 同じ列・同じ行・同じブロック内に同じ数字が入っていない
例えば下記の 2×2 の数独問題を解く場合は、

下の図のように空いているマスに対して数字の配置の全パターンを1つずつ、解として成立しているかを調べていきます(黒色の数字は最初から配置されている数字を表しています)。
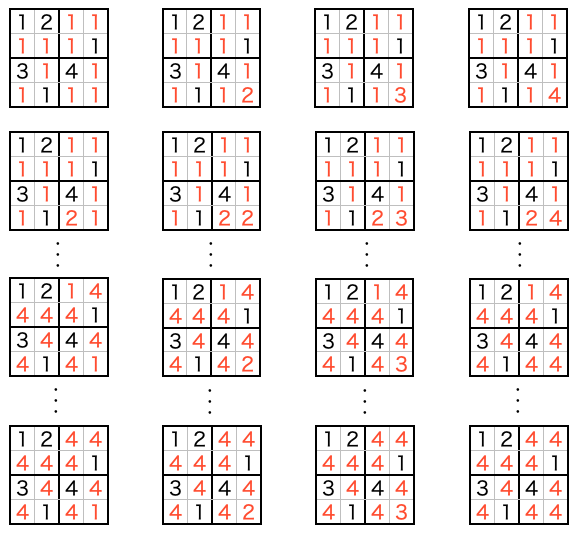
考え方は簡単ですが、特に空いているマスが多いとパターン数が多くなってしまい、解を見つけ出すのに時間がかかってしまいます。
バックトラック法で解く
次に説明する方法は「バックトラック法で解く」です。根本の考え方は「全パターンを総当たりで調べる」と同じですが、バックトラック法を用いることで、調べるパターン数を減らすことができます。
バックトラック法とは
バックトラック法とは下記のような手法です。
「どんどん手を進めて組み合わせを作成していき、途中でその組み合わせが解になり得ないと分かった時に、手を戻して別の組み合わせを作成する」
バックトラック法の実例
全てのパターンを総当たりで解くで紹介した 2×2 の数独問題についてもう一度考えてみましょう。

全てのパターンを総当たりで調べる場合は下記のように全パターンを調べる方法でした。

ここでよく考えていただきたいのが、下の図のオレンジ枠部分です。
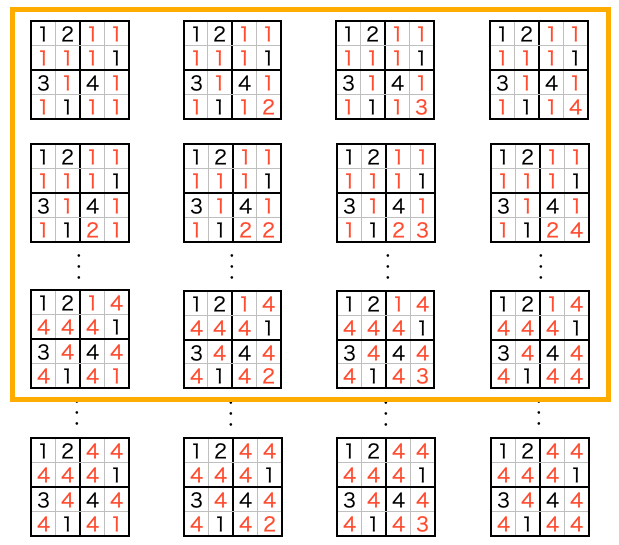
これらのパターンって、調べるまでもなく、下の赤字の場所に 1 を入れた時点で解になり得ないことは明らかですよね?同じ行にも同じブロックにも 1 があるので数独のルールを満たしていません。
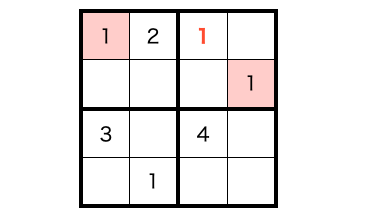
つまり、赤字の場所に 1 を入れたパターンはこれ以上調べても無駄です。なので、赤字の場所に 1 を入れたパターンは調べずにスキップし、その場所に別の数字を入れたパターンを調べてしまっても解を見つけ出すのに支障はありません。
なので、赤字の場所に 1 を入れたパターンが解になり得るかどうかのチェックはスキップし、次に他の数字を入れたパターンについて調べていきます。
このスキップにより「全てのパターンを総当たりで解く」方法では調べる必要があった下図のオレンジ枠内のパターンを調べる処理をスキップすることができることになります。

つまり、このスキップにより調べる必要のあるパターンを減らすことができたことになります。
こんな感じで下記のように調べるパターンを減らすのがバックトラック法です!
- とりあえず数字を1つ入れてみる
- 数字を入れた場合に解になり得るかどうかを調べる
- 解になり得ない場合は入れた数字を取り除き(手を戻し)、次の他の数字を入れてみる
そして、解になり得る場合のみ、次のマスに数字を入れて次のパターンを調べていきます。
数独を解くサンプルプログラム
続いて数独を解くサンプルプログラムの紹介をしていきたいと思います。
スポンサーリンク
ソースコード
このバックトラック法で数独を解くサンプルプログラムのソースコードは下記のようになります。
#include <stdio.h>
/* ボードの幅・高さ・数字の最大値 */
#define NUM 9
/* ブロックの幅・高さ */
#define BLOCK 3
/* BOOL型の定義 */
typedef enum
{
TRUE = 1,
FALSE = 0
} BOOL;
/* ボードの初期状態 */
#if NUM == 9
static int board[NUM][NUM] = {
{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}
};
#elif NUM == 4
static int board[NUM][NUM] = {
{1, 2, 0, 0},
{0, 0, 0, 1},
{3, 0, 4, 0},
{0, 4, 0, 0}
};
#endif
/* 見つかった答えの個数 */
static unsigned int answer = 0;
/* 関数のプロタイプ宣言 */
void showBoard(void);
BOOL putNumber(int, int, int);
BOOL checkNumber(int, int, int);
void start(void);
/**
* 答えとなるボードを表示する
*
* 引数
* なし
*
* 返却値
* なし
*/
void showBoard(void)
{
int i, j;
printf("%u個目の解答です\n", answer);
for (j = 0; j < NUM; j++)
{
for (i = 0; i < NUM; i++)
{
printf("%d ", board[j][i]);
}
printf("\n");
}
printf("\n");
}
/**
* 数字が入れられるかを判断する
*
* 引数
* i:入れる場所(横方向座標)
* j:入れる場所(縦方向座標)
* number:入れる数字
*
* 返却値
* TRUE:入れられる場合
* FALSE:入れられない場合
*/
BOOL checkNumber(int i, int j, int number)
{
int x, y;
int bi, bj;
/* 第j行に同じ数字があるかどうかを判断 */
for (x = 0; x < NUM; x++)
{
if (board[j][x] == number)
{
/* あった場合は入れられない */
return FALSE;
}
}
/* 第i行に同じ数字があるかどうかを判断 */
for (y = 0; y < NUM; y++)
{
if (board[y][i] == number)
{
/* あった場合は入れられない */
return FALSE;
}
}
/* 同じブロック内に同じ数字があるかどうかを判断 */
/* 同じブロックの先頭座標を計算 */
bi = i / BLOCK * BLOCK;
bj = j / BLOCK * BLOCK;
for (y = 0; y < BLOCK; y++)
{
for (x = 0; x < BLOCK; x++)
{
if (board[bj + y][bi + x] == number)
{
/* あった場合は入れられない */
return FALSE;
}
}
}
/* 同じ行・同じ列・同じグループに同じ数字がない場合 */
return TRUE;
}
/**
* 数字をボードに入れる
*
* 引数
* i:入れる場所(横方向座標)
* j:入れる場所(縦方向座標)
* number:入れる数字
*
* 返却値
* TRUE:入れられた場合
* FALSE:入れられなかった場合
*/
BOOL putNumber(int i, int j, int number)
{
int fix_flag = FALSE;
/* 最初から(i, j)座標にnumberが入っているかを確認 */
if (board[j][i] != number)
{
/* 入っているのがnumber以外の場合 */
/* number以外の数字が入っているかを確認 */
if (board[j][i] != 0)
{
/* 異なる数字が入っている場合は入れられない */
return FALSE;
}
/* (i, j)座標にnumberが入れたパターンが解になり得るかを確認 */
if (!checkNumber(i, j, number))
{
/* 解になり得ない場合はこのパターンを調べても無駄 */
return FALSE;
}
/* (i, j)座標にnumberを入れる */
board[j][i] = number;
}
else
{
/* 最初から入ってた場合はフラグを立てておく */
fix_flag = TRUE;
}
/* 全マスに数字を入れたかを確認 */
if (i == NUM - 1 && j == NUM - 1)
{
/* 解の数をカウントアップ */
answer++;
/* 結果を表示 */
showBoard();
}
else
{
/* まだ入れていないマスがある場合 */
int n;
int next_i, next_j;
/* 次の行に移るかを確認 */
if (i + 1 >= NUM)
{
/* 次に数字を入れる場所を次の行に設定 */
next_i = 0;
next_j = j + 1;
}
else
{
/* 今の行のまま次に数字を入れる場所を設定 */
next_i = i + 1;
next_j = j;
}
/* 次のマスに数字を入れてみる */
for (n = 1; n <= NUM; n++)
{
putNumber(next_i, next_j, n);
}
}
/* numberが最初から入れられていたかを確認 */
if (!fix_flag)
{
/* 入れた数字を取り除く */
board[j][i] = 0;
}
return TRUE;
}
/**
* 数独を開始する
*
* 引数
* なし
*
* 返却値
* なし
*/
void start(void)
{
int n;
for (n = 1; n <= NUM; n++)
{
/* (0, 0)座標に数字nを入れてゲーム開始 */
putNumber(0, 0, n);
}
}
int main(void)
{
start();
printf("回答数:%u\n", answer);
return 0;
}
実行方法
まず必要に応じて NUM・BLOCK の定義値と board 配列の初期値を設定してください。
詳細は次のサンプルプログラムの解説で説明しますが、これらを変更することでマスの数・グループの数・マスに最初から入れられている数字を設定することができます。
解きたい数独問題に合わせてこれらの値を設定してください。ただし、board 配列の初期値では、解が存在し得るように値を設定してください(同じ行・同じ列・同じブロックに 0 以外の同じ数字があると、おそらくプログラムは上手く動作してくれません)。
あとはコンパイルしてプログラムを実行すれば良いだけです。
例えばターミナルやコマンドプロンプト等のコマンドラインから gcc でコンパイルしてプログラムを実行するためには、下記のようにコマンドを実行すれば良いはずです。
gcc main.c -o main.exe ./main.exe
実行すれば、設定した数独問題の解が下記のように表示されます。
1個目の解答です 5 3 4 6 7 8 9 1 2 6 7 2 1 9 5 3 4 8 1 9 8 3 4 2 5 6 7 8 5 9 7 6 1 4 2 3 4 2 6 8 5 3 7 9 1 7 1 3 9 2 4 8 5 6 9 6 1 5 3 7 2 8 4 2 8 7 4 1 9 6 3 5 3 4 5 2 8 6 1 7 9 解答数:1
解が複数ある場合は、複数の解が表示されます。
サンプルプログラムの解説
最後にサンプルプログラムの解説をしておきます。
スポンサーリンク
数字の配置を管理する配列を作成する
各マスに何の数字が入れられているかを管理するために、下記の二次元配列 board を作成しています。
/* ボードの初期状態 */
#if NUM == 9
static int board[NUM][NUM] = {
{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}
};
#elif NUM == 4
static int board[NUM][NUM] = {
{1, 2, 0, 0},
{0, 0, 0, 1},
{3, 0, 4, 0},
{0, 4, 0, 0}
};
#endif0 は数字がまだ入っていないことを表し、0 以外の値は、その数字がマスに入っていることを示すようにしています。
上記のように配列初期化時に 0 以外の値を配列に格納することで、最初からマスに数字が入った数独問題を解くことができます(基本的に数独問題では最初から複数のマスに数字が入っており、それをヒントに問題を解いていくことになります)。
NUM はマスの縦方向および横方向のマス数および、入れられる数字の最大値を表しています(1 〜 NUM の数字が入れられる)。
ですので、この NUM の値の定義を変更することで、解きたい数独のマス数を変更できるようになります。また、マスに入れられる数字は 1 〜 NUM の間の NUM 種類の数字になります(上記では NUM が 9 の場合と NUM が 4 の場合の board の宣言を行っています)。
/* ボードの幅・高さ・数字の最大値 */
#define NUM 9また BLOCK はブロックの縦方向および横方向のマス数を表すようにしています。NUM の平方根の値を BLOCK に設定することを想定しています。NUM の値に応じて適宜値を設定してください。
/* ブロックの幅・高さ */
#define BLOCK 3座標 (i, j) のマスに入っている数字を取得したり、座標 (i, j) のマスに数字を入れるには、下記のようにして座標 (i, j) のマスにアクセスします。
board[j][i] = 5;
printf("%d\n", board[j][i]);数独のゲームを進める際に、座標 (i, j) のマスに数字を入れる場合は board[j][i] に 0 以外の数字を入れ、マスから数字を取り除く場合は board[j][i] に 0 を入れるようにすることで、board で数字の配置を管理できるようになります。
解になり得るかを調べる(checkNumber)
また、解になり得るパターンであるかどうかを調べられるように checkNumber 関数を用意しています。
checkNumber の引数は下記の3つで、現在の数字の配置(board で管理)に対して、引数で指定した座標 (i, j) のマスに number を入れた場合に、解になり得るかどうかを判断する関数になります。
- 第1引数
i:数字を入れるマスの座標(横方向) - 第2引数
j:数字を入れるマスの座標(縦方向) - 第3引数
number:マスに入れる数字
解になり得る場合は TRUE、なり得ない場合は FALSE を返却します。
要は、座標 (i, j) と同じ列・同じ行・同じブロックに、既に number と同じ数字が入れられていないかを board を参照して調べる関数です。
数字をマスに入れる(putNumber)
putNumber 関数は実行時点の board 配列(数字の配置)に対し、新たに数字を入れる関数です。
putNumber の引数は下記の3つで、board 配列に対し、引数で指定した座標 (i, j) に number を入れる関数になります。
- 第1引数
i:数字を入れるマスの座標(横方向) - 第2引数
j:数字を入れるマスの座標(縦方向) - 第3引数
number:マスに入れる数字
数字を入れられた場合は TRUE、入れられなかった場合は FALSE を返却します(結局プログラム内では使用していないので戻り値はなしでもよかったと思ってます…)。
putNumber 関数の大まかな処理は下記のようになります。
- 座標 (
i,j) のマスにnumberを入れたパターンが解になり得るかをcheckNumberで調べる - 解になり得ない場合は直ちに関数を終了する
- 座標 (
i,j) のマスにnumberを入れる - 3. により全マスに数字が入ったかどうかを確認
- 全マスに数字が入っている場合:その時点の数字の配置が解なので、結果を
showBoard関数で表示する - 全マスに数字が入っていない場合:次のマスに数字を入れたパターンを調べるために
putNumber関数を実行する
- 全マスに数字が入っている場合:その時点の数字の配置が解なので、結果を
- 座標 (
i,j) のマスから数字を取り除く
他にも最初から数字が入っていた場合に、数字を入れる処理をスキップするなどの処理も行なっていますが、大まかな流れは上記の通りだと思います。
putNumber 関数のポイントになる部分は下記の3点だと思います。
再帰呼び出しで数字を入れていく
putNumber 関数では、マスに数字を入れた後に、次のマスに数字を入れるために自分自身の putNumber 関数を実行するようにしています。
つまり再帰呼び出しを行なっていきます。
/* 次の行に移るかを確認 */
if (i + 1 >= NUM)
{
/* 次に数字を入れる場所を次の行に設定 */
next_i = 0;
next_j = j + 1;
}
else
{
/* 今の行のまま次に数字を入れる場所を設定 */
next_i = i + 1;
next_j = j;
}
/* 次のマスに数字を入れてみる */
for (n = 1; n <= NUM; n++)
{
putNumber(next_i, next_j, n);
}putNumber 関数を実行することで、指定した引数に応じてマスに数字が入れられます。
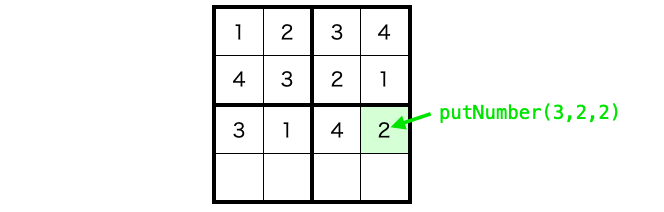
さらに、上記のようにマスの座標を次の座標に移動させながら putNumber 関数を実行するようにすることで、次のマスにも数字が入れられることになります。
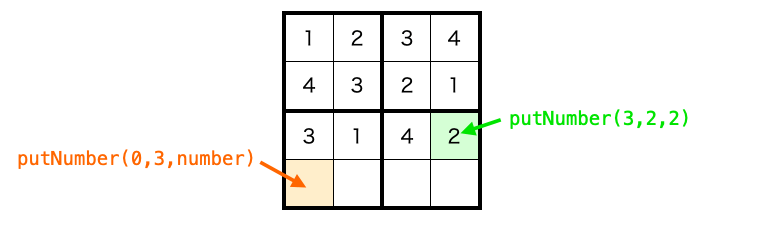
さらにさらに、その putNumber 関数の中でもマスに数字が入れられ、次のマスに対して putNumber 関数が実行されます。
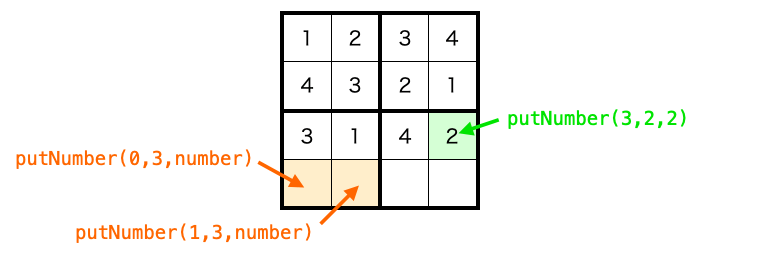
こんな感じで putNumber 関数の中でマスを移動させながら putNumber 関数を実行することで、最後のマスまで数字を入れることができます。
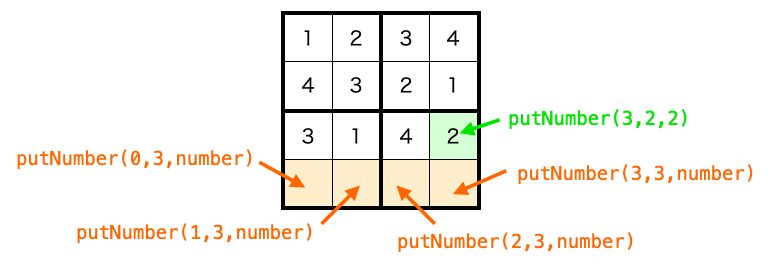
また、putNumber 内で putNumber を実行する時に入れる数字(引数 number)も 1 〜 NUM の全パターンをループで試すようにしています。
したがって、putNumber(i , j, number) が実行するだけで、座標 (i, j) よりも後ろ側のマスに対して全てのパターンを試すことになります。
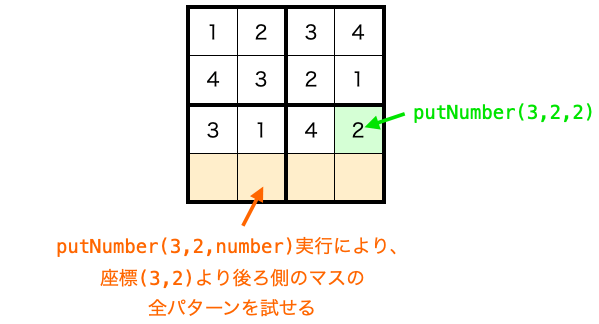
なので、最初に座標 (0,0) に対して 1 〜 NUM の数字を入れるように putNumber 関数を実行することで、全マスに対して全パターンの数字の配置を試すことができることになります。
これを実行しているのが start 関数になります。
void start(void) {
int n;
for (n = 1; n <= NUM; n++) {
/* (0, 0)座標に数字nを入れてゲーム開始 */
putNumber(0, 0, n);
}
}数字を入れる前に数字を入れたパターンが解になり得るかをチェックする
ただし、これだけだと「全パターンを総当たりで解く」のと同じです。
今回実装しているのは「バックトラック法で解く」方法ですので、putNumber 関数では、上記の再起呼び出しを単に行うだけでなく、マスに数字を入れる前に checkNumber 関数で「数字を入れた場合に解になり得るかどうか」を調べ、解になり得る場合のみ実際にマスに数字を入れるようにしています。
/* (i, j)座標にnumberが入れたパターンが解になり得るかを確認 */
if (!checkNumber(i, j, number))
{
/* 解になり得ない場合はこのパターンを調べても無駄 */
return FALSE;
}
/* (i, j)座標にnumberを入れる */
board[j][i] = number;バックトラック法の解説では「とりあえず数字を入れてみる」→「数字を入れた場合に解になり得るかどうかを調べる」の順序で説明しましたが、サンプルプログラムでは「数字を入れた場合に解になり得るかどうかを調べる」→「なり得る場合のみ数字を入れる」ように実装しています
これはこっちの方がソースコードを書きやすかったからです
順序は異なりますがバックトラック法の考え方は踏襲しています
上記の制御を行うことで、解になり得ない場合は、マスに数字を入れることなく即座に関数を終了する様になります。
次のマスに対する putNumber 関数の再起呼び出しも行いません。
なので、現状の数字の配置(board)対して座標 (i, j) のマスに number を入れるパターンの配置を調べる処理はこの時点で終了します。
このように、調べても無駄なパターンはもう試さないようにすることで調べるパターン数を減らしています。
putNumber 関数では最後のマスを目指してどんどんマスに数字を入れていきますが、バックトラック法により途中で解になり得ないパターンを調べるのをやめますので、実際に putNumber 関数で最後のマスに数字が入れられるのは解のパターンのみになります。
最後に数字を取り除く
putNumber 関数で下記の処理が完了したということは、
/* 次のマスに数字を入れてみる */
for (n = 1; n <= NUM; n++)
{
putNumber(next_i, next_j, n);
}座標 (i, j) のマスに number を入れた場合の全パターンが、解になり得るかどうかの確認が完了したことになります。
ですので、続いて座標 (i, j) のマスに新たな数字を入れるパターンを調べるために、関数の最後で下記を実行して座標 (i, j) のマスから number を取り除く(そのマスを空にする)ようにしています。
/* numberが最初から入れられていたかを確認 */
if (!fix_flag)
{
/* 入れた数字を取り除く */
board[j][i] = 0;
}ただし最初から数字が入っている場合は取り除かないように if 文で場合分けするようにしています(詳細は fix_flag を使用している箇所のソースコードを読んでみてください)。
スポンサーリンク
まとめ
このページでは、 数独(ナンプレ)をC言語プログラミングで解く方法について解説しました!
数独のように「解となり得るパターンを見つけ出すゲーム」に関しては、基本的に全パターンの組み合わせに対して「解になり得るかどうか」をチェックしてやれば問題を解くことができます。
ただし、全パターンを試すと時間がかかるので、今回紹介したバックトラック法等を用いてパターン数を減らすことで、問題を解く時間を短縮することができます。
数独問題を解くプログラムは、パズルを解く感覚でプログラミングできますし、再帰呼び出しやバックトラック法を理解するのにも良い題材だと思います。
是非皆さんもプログラミングで数独を解くのに挑戦してみてください!
また今回紹介したバックトラック法はいろんなパズルを解くのに使用されているアルゴリズムです。
私のサイトでも下記ページでバックトラック法を用いたプログラムを公開していますので、バックトラック法に興味がある・もっといろんな場面での使い方を知りたい方は、こちらも是非読んでみてください!
 【C言語】エイトクイーン問題(Nクイーン問題)のバックラック法での解き方
【C言語】エイトクイーン問題(Nクイーン問題)のバックラック法での解き方
 【C言語】ナイト巡回問題(ナイトツアー)のバックラック法での解き方
【C言語】ナイト巡回問題(ナイトツアー)のバックラック法での解き方