【C言語】チェイン法について解説（ハッシュ探索時の衝突を解決する方法）

このページでは “チェイン法” について解説していきます。

チェイン法は、ハッシュ法でのデータ探索時に発生する “衝突を解決するための手法” です。

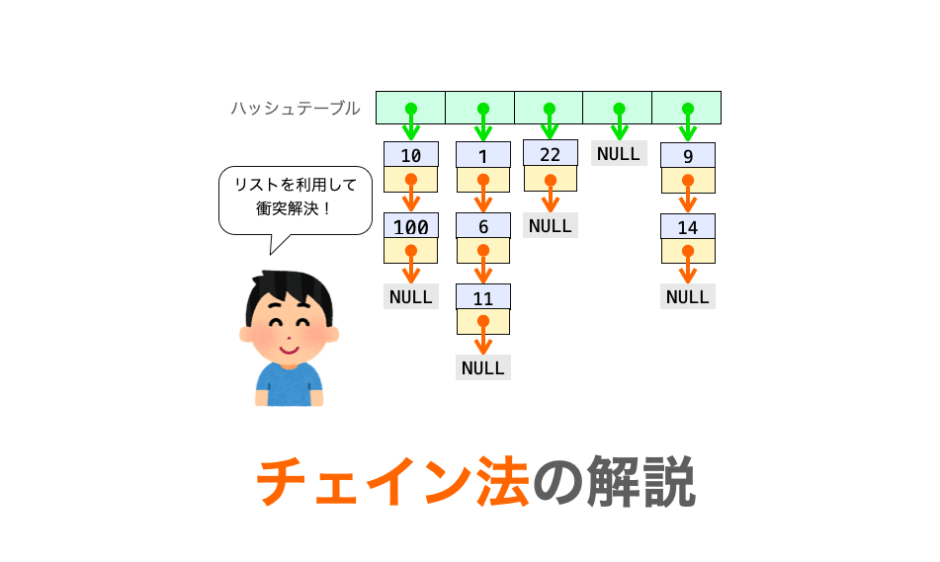
最初に結論を言っておくと、このチェイン法はリストを利用することで衝突を解決する手法になります。

ですので、チェイン法を実装する上ではリストの実装の仕方を知っている必要があります。

リストの実装の仕方については下記ページで解説していますので、もしチェイン法を実装してみたいけどリストの実装の仕方は知らないという方は、是非下記ページを参照していただければと思います。

【C言語】リスト構造について分かりやすく解説【図解】

ハッシュ法と衝突のおさらい

まずチェイン法を理解するためには、ハッシュ法とハッシュ法で発生する衝突について理解しておく必要があります。

ということで、まずは簡単にハッシュ法と衝突のおさらいをしておきたいと思います。

詳細については下記ページで解説していますので、詳しく知りたい方は下記ページをご参照していただければと思います。

【C言語】ハッシュ法（データ探索アルゴリズム）について分かりやすく解説

ハッシュ法とは

ハッシュ法は、探索したいデータに対してハッシュ関数を実行してハッシュ値を求め、そのハッシュ値の位置（そのハッシュ値を添字とする配列の位置）を探索するアルゴリズムになります。

さらに、ハッシュ法ではデータ格納時にも同じハッシュ関数を利用します。

具体的には、格納したいデータに対してハッシュ関数を実行してハッシュ値を求め、そのハッシュ値の位置にデータを格納します。

ハッシュ関数は同じ入力データに対して同じハッシュ値が算出されるように作成されますので、探索したいデータが格納されている位置はハッシュ関数によって求められることになります。

なので、ハッシュ関数を実行し、その位置さえ調べれば探索は完了になります。

用語についてもおさらいしておくと、ハッシュ法におけるデータを格納する配列をハッシュテーブルと呼び、このハッシュテーブルの各要素をバケットと呼びます。

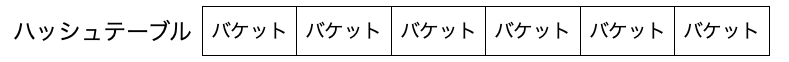
スポンサーリンク

衝突とは

ただし、ハッシュ関数によって算出されるハッシュ値は異なる入力データであっても重複する可能性があります。

このとき、同じハッシュ値が算出されてしまった複数のデータのうち１つを除いてバケットには格納することができません（配列の１つの要素に格納できるデータは１つのみですよね？）。

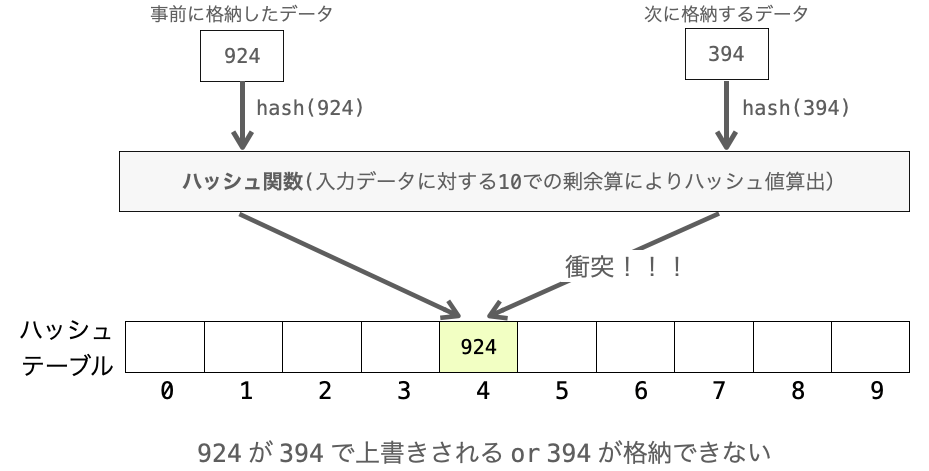
この場合、バケットに格納されなかったデータはハッシュテーブル内に存在しないことになります。ですので、当然格納されなかったデータを後から探索したとしても探索に必ず失敗することになります。

本来ハッシュテーブルに格納したはずのデータであるはずなのに、探索に失敗することになりますので、探索の動作が異常であるといえます。

このように、ハッシュ法においてハッシュ値が重複してしまうことを衝突と呼びます。単なるハッシュ法では、衝突が発生した場合は探索の動作が異常になります。

ですので、衝突が発生した時にも探索を正常に動作させるためには、そのための対応が必要になります。

その対応の手法の１つが、今回紹介するチェイン法になります。

ちなみに、別の手法であるオープンアドレス法については、先ほども紹介した下記ページで解説していますので、オープンアドレス法について知りたい方は是非下記ページを参照していただければと思います。

【C言語】ハッシュ法（データ探索アルゴリズム）について分かりやすく解説

チェイン法

続いては、このページでの本題になるチェイン法について解説していきます。

チェイン法とは

チェイン法は、前述でおさらいした “ハッシュ法における衝突” が発生した時にも探索を正常に動作させるための手法の１つになります。

その具体的な方法は、”各バケットをリストとして扱う” です。チェイン法においては、ハッシュテーブルに存在するバケットの数だけリストを用意し、そのリストによってデータの管理を行います。

要は、チェイン法におけるハッシュテーブルはリストの配列となります。

ただし、C言語 の場合はリストの先頭のノードのアドレスを用いてリストを管理するため、各リストの先頭ノードのアドレスを格納する配列と考えても良いと思います。

イメージとしては、下の図のように各バケットにリストの先頭ノードのアドレスが格納されており、そこからノードがぶら下がっていく感じです（都合上 NULL を別のものとして記述していますが、実際は全ての NULL は同じものです）。

前述でも解説した通り、単なるハッシュ法の場合、バケットは配列の要素として扱っていましたが、配列の場合、各要素に格納できるデータは基本的に１つだけです。ですので、衝突が発生すると探索が正常に行えなくなってしまっていました。

その一方でチェイン法の場合、複数のデータで衝突が発生したとしても、それらの全てのデータをリストのノードとして保持することができます（リストの実現方法にもよりますが、ノードを malloc 関数を使って作成する場合はメモリが足りる限りリストにノードとして追加することができます）。

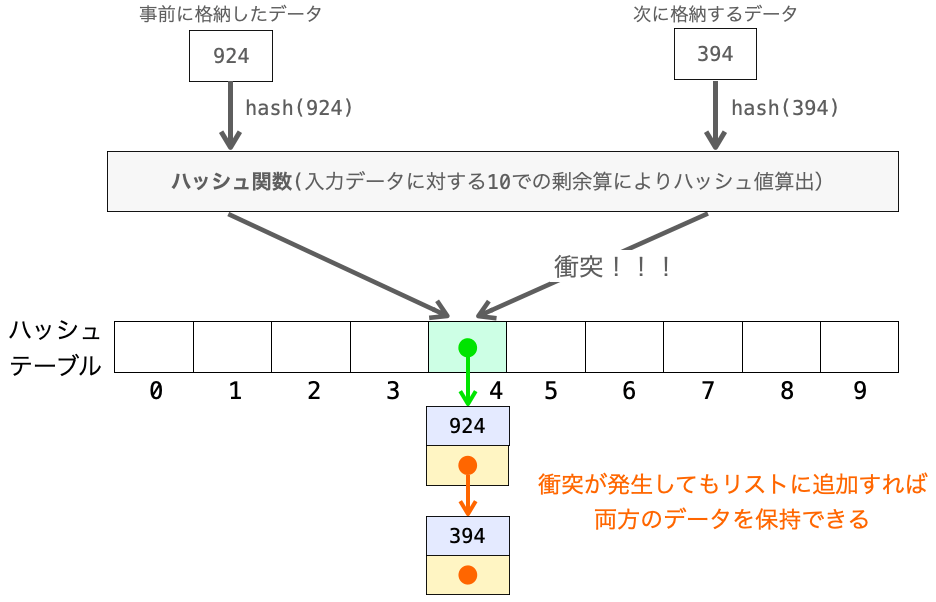
つまり、ハッシュテーブルの中に衝突が発生した全てのデータが保持されることになるので、衝突が発生したようなデータであっても後から探索することが可能です。

スポンサーリンク

チェイン法におけるデータの格納

ここからは、チェイン法におけるデータの操作をどのようにして行うかについて、もう少し詳細に解説していきたいと思います。

まずチェイン法でデータの格納を行う際には、ハッシュ法同様にハッシュ値を算出し、さらにそのハッシュ値に対応するバケットのリストにそのデータをノードとして追加します。

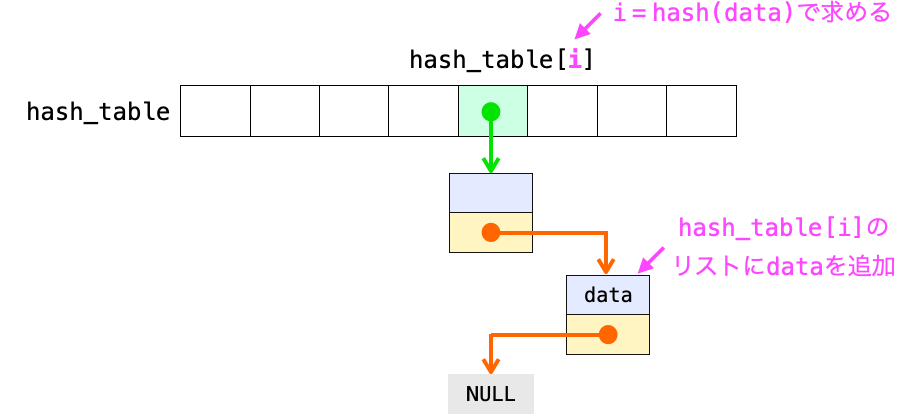
そのバケットのリストが空の場合、そのノードが先頭のノードとして追加されますし、空でない場合は、そのノードがリストのいずれかの位置に追加されます（どの位置に追加されるかはリストへのノードの追加を行う関数の作り方による）。

どちらの場合であっても、リストに追加することはできますので、ハッシュ値の重複があったとしても、それにより一方のデータが失われるようなことはありません。

チェイン法におけるデータの探索

さらに、チェイン法でデータの探索を行う際には、ハッシュ法同様にハッシュ値を算出し、さらにそのハッシュ値に対応するバケットのリストからそのデータを持つノードの探索を行います。

ハッシュ値に対応するバケットさえ特定できれば、あとは単純にデータを指定してリストから探索を行えば良いだけですので、要はリストからのノードの探索が実現できれば簡単に実現できます。

チェイン法におけるデータの削除

データの削除もここまでに紹介した操作同様で、ハッシュ法同様にハッシュ値を算出し、さらにそのハッシュ値に対応するバケットのリストからそのデータを持つノードの削除を行います。

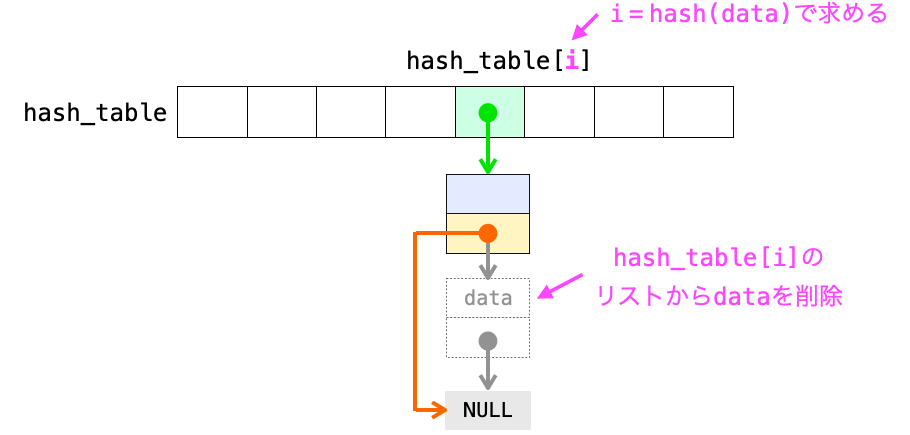
ハッシュ値に対応するバケットさえ特定できれば、あとは単純にデータを指定してリストから削除を行えば良いだけですので、要はリストからのノードの削除が実現できれば簡単に実現できます。

ここまでデータの追加・データの探索・データの削除の仕方を解説してきましたが、いずれもハッシュ値の算出によりバケットさえ特定できれば、あとはそのバケットのリストのノードへの操作を行えば良いだけですので、基本的にリストが既に実現できれば簡単にチェイン法を実現することができます。

リストのノードへの各操作の詳細は下記ページで解説していますので、必要に応じて下記ページを参照していただければと思います。

【C言語】リスト構造について分かりやすく解説【図解】

スポンサーリンク

チェイン法のサンプル実装

それでは、チェイン法のサンプル実装を紹介していきたいと思います。

ソースコードは chain.c と list.c の２つに分かれており、これらのファイルから list.h をインクルードしています。

ソースコードは２つなので、分割コンパイルを行う必要があります。例えば gcc でコンパイルする場合は、下記を実行することでコンパイルが完了し、chain.exe が作成されるはずです。

gcc chain.c list.c -o chain.exe

list.h

チェイン法のサンプル実装における list.h は下記のようになります。

/* ノードを表現する構造体 */
struct NODE {
    int data; /* 管理するデータ */
    struct NODE *next; /* 次のノード */
};

int add(struct NODE **, int);
int delete(struct NODE **, int);
struct NODE * search(struct NODE *, int);

上記の list.h で行なっているのは、ノード構造体の定義と list.c で定義するリスト関連の関数のプロトタイプ宣言の２つです。

後者に関しては見ていただければ分かると思いますのでここでは説明は省略します。

ノード構造体の定義

チェイン法ではリストを使用しますので、そのリストのノードを表現する構造体を NODE 構造体として定義しています。

struct NODE {
    int data; /* 管理するデータ */
    struct NODE *next; /* 次のノード */
};

data がハッシュテーブルに格納するデータそのものであり、next はそのノードの次の位置のノードを示すポインタになります。今回は data は単に int 型の整数としていますが、必要に応じてここは変更していただければと思います（それに合わせて chain.c と list.c の変更も必要になります）。

list.c

チェイン法のサンプル実装における list.c は下記のようになります。

#include <stdlib.h>
#include "list.h"

/******************************
 * リストにノードを追加する関数
 * number：追加するノードの会員番号
 * name：追加するノードの会員名
 * 返却値：0（成功時）
 *      ：-1（失敗時）
 ******************************/ 
int add(struct NODE **head, int data){
    struct NODE *new; /* 追加するノードのアドレス */
    struct NODE *node; /* 今注目しているノードのアドレス */
    struct NODE *prev; /* nodeの前のノードのアドレス */

    /* ノードを新規追加 */
    new = (struct NODE*)malloc(sizeof(struct NODE));
    if (new == NULL) {
        return -1;
    }

    new->data = data;

    /* リストの先頭のノードに注目 */
    node = *head;

    /* ノードを追加する位置を決める */
    while (node != NULL) {
        
        /* nodeを前のノードとして覚えておく */
        prev = node;

        /* 次のノードを辿る */
        node = node->next;
    }

    if (node == *head) {
        /* 追加する位置がリストの先頭の場合 */

        /* 元々先頭だったノードをnewの次のノードにする */
        new->next = *head; /* リストが空の場合はheadはNULL */

        /* リストの先頭をnewとする */
        *head = new;

    } else {
        /* 追加する位置がリストの先頭以外の場合 */

        /* prevとnodeの間にnewを追加 */
        prev->next = new;
        new->next = node; /* 追加する位置が末尾の場合ははnodeはNULLになっている */
    }

    return 0;
}

/******************************
 * リストからノードを削除する関数
 * targetr：削除するノードの会員番号
 * 返却値：0（成功時）
 *      ：-1（失敗時）
 ******************************/ 
int delete(struct NODE **head,int target){
    struct NODE *node; /* 今注目しているノードのアドレス */
    struct NODE *prev; /* nodeの前のノードのアドレス */

    if (*head == NULL) {
        /* リストが空なら何もしない */

        return -1;
    }

    /* リストの先頭のノードに注目 */
    node = *head;

    if (node->data == target) {
        /* 削除対象がリストの先頭のノードの場合 */

        /* リストの先頭をnodeの次のノードにしてnodeを削除 */
        *head = node->next;
        free(node);

        return 0;
    }

    while (node != NULL) {

        if (node->data == target) {
            /* 削除対象のノードが見つかった */

            /* prevの次のノードをnodeの次のノードに設定 */
            prev->next = node->next;

            /* 削除対象のノードを削除して終了 */
            free(node);

            return 0;
        }

        /* nodeを前のノードとして覚えておく */
        prev = node;

        /* 次のノードを辿る */
        node = node->next;

    }

    /* targetを持つノードが見つからなかった */
    return -1;
}

/******************************
 * リストからノードを探索する関数
 * target：探索するノードの会員番号
 * 返却値：見つかったノードのアドレス（成功時）
 *      ：NULL（失敗時）
 ******************************/ 
struct NODE * search(struct NODE *head, int target){
    struct NODE *node; /* 今注目しているノードのアドレス */

    /* リストの先頭のノードに注目 */
    node = head;

    while (node != NULL) {

        if (node->data == target) {
            /* 探索したいノードが見つかった */

            return node;
        }

        /* 次のノードを辿る */
        node = node->next;

    }

    /* targetを持つノードが見つからなかった */
    return NULL;
}

list.c では、リストのノードへの操作を行う下記の３つの関数を定義しています。

• add：リストにノードを追加する
• delete：リストからノードを削除する
• search：リストからノードを探索する

これらの関数の動作は下記のページで紹介しているものとほぼ同様になります。ですので、これらの関数がどのような処理を行なっているかは下記ページをご参照していただければと思います。

【C言語】リスト構造について分かりやすく解説【図解】

ですが、list.c で定義している関数では、上記のページで紹介している関数から次の３点を変更しているので注意してください。

• NODE 構造体の定義の違いに伴う変更
• リストの先頭ノードのアドレスを引数で受け取るように変更
• リストへのノード追加はリストの末尾に行うように変更

ここからは、上記ページと対比する形で、この list.c の内容について解説していきたいと思います（以降では、上記ページを 参考ページ と呼ばせていただきます。

NODE 構造体の定義の違いに伴う変更

まず list.c で使用する NODE 構造体は、前述の通り次のように定義しています。

struct NODE {
    int data; /* 管理するデータ */
    struct NODE *next; /* 次のノード */
};

その一方で、参考ページ で使用している NODE 構造体の定義は次のようになります。

struct NODE {
    int number; /* 会員番号 */
    char name[256]; /* 会員名 */
    struct NODE *next; /* 次のノード */
};

このように NODE 構造体のメンバが異なるので、それに応じて各関数の変更を行なっています。

例えば、参考ページ の search 関数では、次のように引数 target が各ノードの number メンバと一致するかどうかを調べることでデータの探索を行なっています。

if (node->number == target) {
    /* 略 */
}

その一方で、list.c では、引数 target が各ノードの data メンバと一致するかどうかを調べることでデータの探索を行なっています。

if (node->data == target) {
    /* 略 */
}

このような NODE 構造の違いに伴う変更を、各関数において行なっていますので注意してください。

リストの先頭ノードのアドレスを引数で受け取るように変更

また、参考ページ においては、リストの先頭ノードのアドレスはグローバル変数 head で管理するようにしていました。

そのため、参考ページ で紹介している各関数ではリストの先頭ノードのアドレスを引数で受け取る必要がありませんでした。

ただし、これだと複数のリストを扱いづらいので、list.c で定義する関数ではリストの先頭ノードのアドレスを引数で受け取るようにしています。

例えば add 関数の引数は下記のようになります。

add(struct NODE **head, int data)

単にリストの先頭ノードのアドレスではなく、”リストの先頭ノードのアドレスを格納したポインタ変数” のアドレスを引数で受け取るようにしているところがポイントです。

具体的には head の型が struct NODE * ではなく struct NODE ** になっています。

これは、関数内でリストの先頭ノードのアドレスを変更できるようにするためです。

C言語 では、関数に引数として与えられるデータは、関数呼び出し元の変数の中身をコピーしたものになります。

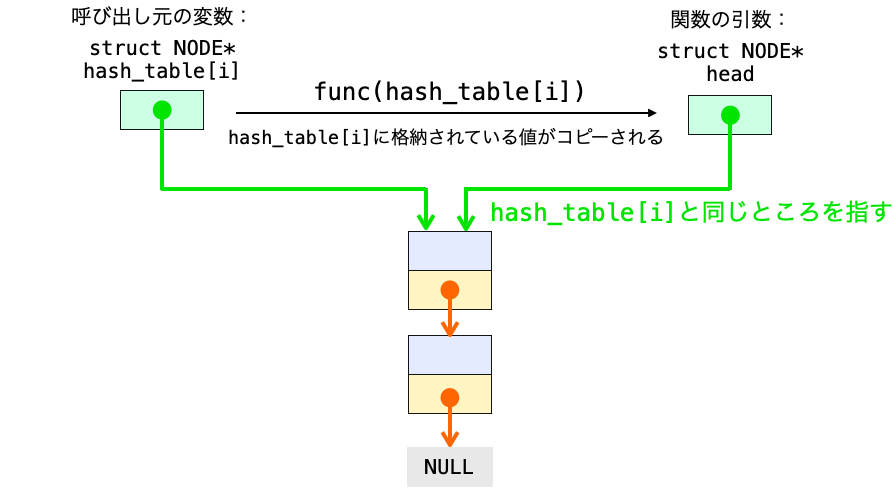
ですので、単にリストの先頭ノードのアドレスを引数として受け取った場合、その引数を変更しても関数呼び出し元の変数には影響しません。

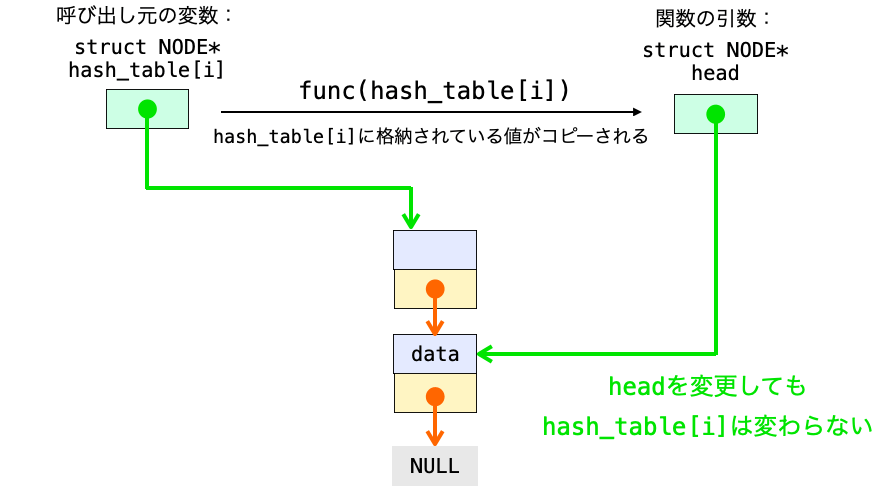
そのため、単にリストの先頭ノードのアドレス（strcut NODE *）を受け取るのではなく、そのアドレスを格納したポインタ変数のアドレスを引数 head で受け取るようにしています（strcut NODE * 型のポインタ変数のアドレスなので struct NODE ** となる）。

つまり、head は “リストの先頭ノードのアドレスが格納された変数” を指すことになります。

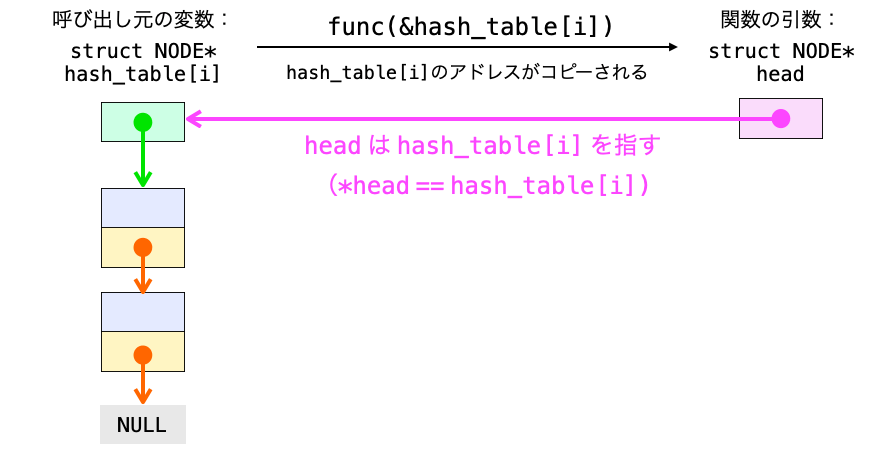
この head の指すデータ（*head）は関数呼び出し元で管理しているリストの先頭ノードのアドレスと全く同じものになるので、関数内でこれを変更すれば関数呼び出し元で管理しているリストの先頭ノードのアドレスも変更することができます。

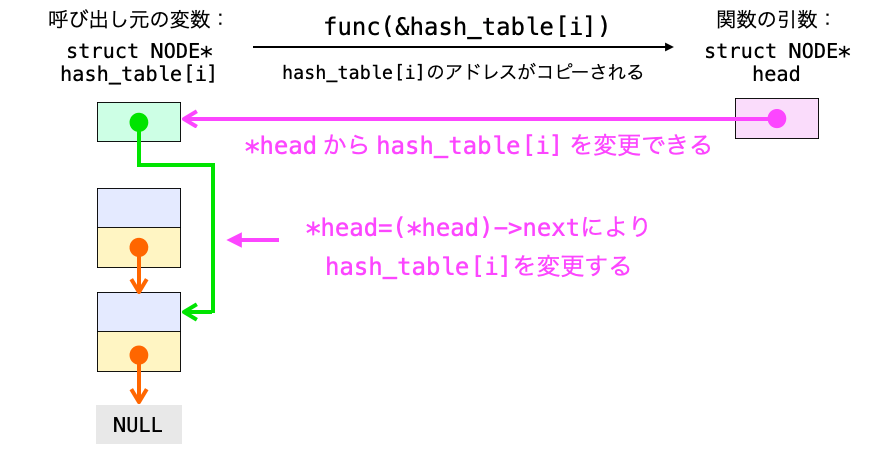
また、このように引数 head を受け取るため、add や delete 関数内の処理においては、リストの先頭ノードのアドレスを参照する際には単に head ではなく、間接演算子を用いて *head と指定するように変更しています。

その一方で、search 関数の場合、リストの先頭ノードのアドレスの変更は行いませんので、単にリストの先頭ノードのアドレス（struct NODE * 型の変数）を受け取るようにしており、単に head と指定するだけでリストの先頭ノードのアドレスを参照することができます。

リストへのノード追加はリストの末尾に行うように変更

さらに、参考ページ のノードの追加を行う add 関数においては、各ノードが昇順に並ぶようにノードを追加する位置を決めるようにしています。

これは、add 関数の while ループを、下記のように if (node->number > new->number) の条件を満たした際に終了するようにすることで実現しています。

/* ノードを追加する位置を決める */
while (node != NULL) {
    if (node->number > new->number) {
        /* 追加する位置が見つかった */
        break;
    }

    /* nodeを前のノードとして覚えておく */
    prev = node;

    /* 次のノードを辿る */
    node = node->next;
}

その一方で、list.c で定義している add 関数においては、追加したノードがリストの末尾のノードになるようにノードを追加する位置を決めるようにしています。

これは、add 関数の while ループを下記のように変更することで実現しています。

/* ノードを追加する位置を決める */
while (node != NULL) {

    /* nodeを前のノードとして覚えておく */
    prev = node;

    /* 次のノードを辿る */
    node = node->next;
}

要は、下記のループ終了条件を無くしているだけです（これにより while ループ終了時に prev が必ずリストの末尾のノードを指すようになる）。

if (node->number > new->number) {
    /* 追加する位置が見つかった */
    break;
}

スポンサーリンク

chain.c

最後に chain.c を紹介していきます。チェイン法のサンプル実装における chain.c は下記のようになります。

#include <stdio.h>
#include "list.h"

/* ハッシュテーブルのサイズ */
#define NUM_BUCKET 10

/* ハッシュテーブル（各要素はリストの先頭を指すポインタ） */
static struct NODE *hash_table[NUM_BUCKET];

/******************************
 * ハッシュ値を算出する関数
 * data：ハッシュ値の元になるデータ
 * 返却値：算出したハッシュ値
 ******************************/ 
unsigned int hash(int data) {
    unsigned int u_data = data;

    return u_data % NUM_BUCKET;    
}

/******************************
 * ハッシュテーブルを初期化する関数
 ******************************/ 
void hash_initialize(void) {
    int i;

    for (i = 0; i < NUM_BUCKET; i++) {
        hash_table[i] = NULL;
    }
}

/******************************
 * ハッシュテーブルの終了処理を行う関数
 ******************************/ 
void hash_finalize(void) {
    int i;

    for (i = 0; i < NUM_BUCKET; i++) {
        
        /* 各バケットが空になるまでノードの削除を繰り返す */    
        while (hash_table[i] != NULL) {
            
            delete(&hash_table[i], hash_table[i]->data);
        }
    }
}

/******************************
 * ハッシュテーブルにデータを追加する関数
 * data：追加したいデータ
 * 返却値：0（成功時）
 *      ：-1（失敗時）
 ******************************/ 
int hash_add(int data) {
    unsigned int i;

    /* ハッシュ値の算出 */
    i = hash(data);

    if (i >= NUM_BUCKET) {
        return -1;
    }

    /* ハッシュ値の位置のバケットのリストにデータ格納 */
    return add(&hash_table[i], data);

}

/******************************
 * ハッシュテーブルからデータを探索する関数
 * data：探索したいデータ
 * 返却値：見つかった位置のアドレス（成功時）
 *      ：NULL（失敗時）
 ******************************/ 
struct NODE* hash_search(int data) {
    
    unsigned int i;
    
    /* ハッシュ値の算出 */
    i = hash(data);

    if (i >= NUM_BUCKET) {
        return NULL;
    }

    /* ハッシュ値の位置のバケットのリストから探索 */
    return search(hash_table[i], data);

}

/******************************
 * ハッシュテーブルからデータを削除する関数
 * data：削除したいデータ
 * 返却値：0（成功時）
 *      ：-1（失敗時）
 ******************************/ 
int hash_delete(int data) {
    
    unsigned int i;
    
    /* ハッシュ値の算出 */
    i = hash(data);

    if (i >= NUM_BUCKET) {
        return -1;
    }

    /* ハッシュ値の位置のバケットのリストから削除 */
    return delete(&hash_table[i], data);
}

int main(void) {
    unsigned int datas[10] = {
        100, 500, 245, 325, 999,
        0, 199, 1, 98, 777
    };
    int i;

    hash_initialize();

    /* データの格納 */
    for (i = 0; i < 10; i++) {
        if (!hash_add(datas[i])) {
            printf("%d is ADDED\n", datas[i]);
        }
    }

    /* データの探索 */
    for (i = 0; i < 10; i++) {
        if (hash_search(datas[i])) {
            printf("%d is FOUND\n", datas[i]);
        }
    }

    /* データの探索が失敗することを確認 */
    if (hash_search(987)) {
        printf("%d is FOUND\n", 987);
    }
    
    if (hash_search(654)) {
        printf("%d is FOUND\n", 654);
    }

    /* データの削除が失敗することを確認 */
    if (hash_delete(654)) {
        printf("%d is DELETED\n", 654);
    }

    /* データ削除後の探索に成功することを確認 */
    hash_delete(500);
    if (hash_search(0)) {
        printf("%d is FOUND\n", 0);
    }
    hash_add(500);

    /* データの削除 */
    for (i = 0; i < 10; i++) {
        if (!hash_delete(datas[i])) {
            printf("%d is DELETED\n", datas[i]);
        }
    }

    hash_finalize();

    return 0;
}

chain.c では、main 関数および、チェイン法によるハッシュ探索を行うための関数を定義しています。

chain.c における各関数が行う操作は下記の通りです。

• hash：ハッシュ値を算出する
• hash_initialize：ハッシュテーブルを初期化する
• hash_add：ハッシュテーブルにデータを追加する
• hash_delete：ハッシュテーブルからデータを削除する
• hash_search：ハッシュテーブルからデータを探索する
• hash_finalize：ハッシュテーブルの終了処理を行う
• main：上記関数を使用してハッシュ法による探索を行う

各関数が何を行なっているかについて簡単に解説しておきます。

hash

hash は引数で与えられるデータからハッシュ値の算出を行うハッシュ関数になります。

今回は単に、引数で与えられる整数を NUM_BUCKET で割った余りをハッシュ値として算出するようにしています。

hash_initialize

このソースコード先頭付近の下記で、ハッシュテーブルの宣言を行なっています。

/* ハッシュテーブル（各要素はリストの先頭ノードを指すポインタ） */
static struct NODE *hash_table[NUM_BUCKET];

この hash_table の各要素 hash_table[i] には、次に説明する hash_add 関数により “ハッシュ値が i となるデータの格納先となるリスト” の先頭ノードのアドレスが格納されていきます。

ただし、プログラム開始時はハッシュテーブルの全てのバケット（リスト）が空の状態になりますので、この hash_initialize 関数で、各バケットのアドレスを NULL に設定しています。

hash_add・hash_delete・hash_search

これらの関数で行うことは下記の通りです。

• 入力データを引数 data として hash 関数を実行し、ハッシュ値 i を求める
• hash_table[i] のリスト（バケット）に対して下記のいずれかを実行する
  • hash_add の場合は add を実行して引数 data をノードとして追加する
  • hash_delete の場合は delete を実行して引数 data を持つノードを削除する
  • hash_search の場合は search を実行して引数 data を持つノードを探索する

add・delete・search は list.c で定義されている関数です。

要は、hash 関数を実行して引数 data に対応するリスト（バケット）を特定すれば、後はリストを操作する関数を実行することでチェイン法におけるデータの格納・データの削除・データの探索を実現することができます。

list.c の解説でも説明したように、add と delete ではリストの先頭ノードのアドレスを格納するポインタ（つまり hash_table[i]）を関数内で変更するため、第１引数は hash_table[i] ではなく &hash_table[i] を指定する必要があります。

その一方で search ではリストの先頭ノードのアドレスは変更しませんので、第１引数には単に hash_table[i] を指定するだけで良いです。

hash_finalize

hash_finalize ではハッシュテーブルに格納されている全データの削除を行います。

具体的には、ハッシュテーブルの各バケット（リスト）が空になるまでノードの削除を繰り返しているだけです（ノードの削除はリストの先頭から順に実行）。

main

main 関数では、ここまで紹介してきた関数を実行し、ハッシュテーブルへのデータの格納（hash_add）やハッシュテーブルからのデータの探索（hash_search）、さらにはハッシュテーブルからのデータの削除（hash_delete）を行っています。

チェイン法の探索効率

最後にチェインそうにおける探索効率について解説しておきます。

チェイン法はハッシュ法における衝突が発生した時の対応手法ですので、衝突が発生しなかった場合はハッシュ法と探索効率は変わりません。

ですので、衝突が発生しなかった場合の探索時の計算量のオーダーは、ハッシュ法と同様に O(1) です。

ただし、衝突が発生した場合は、そのハッシュ値に対応するリスト（バケット）のノードを先頭から順にたどりながら１つ１つ探索したいデータであるかどうかを調べていく必要があります。

要は、この時の探索は線形探索と同様の処理になります。したがって、衝突が発生した時は当然探索効率は低下することになります（そのリストのノード数を M とすれば、平均 M / 2 回、最悪 M 回の比較が必要）。

衝突が発生した際に線形探索を行うという点では、下記ページでも紹介しているオープンアドレス法と同様です。

【C言語】ハッシュ法（データ探索アルゴリズム）について分かりやすく解説

ですが、オープンアドレスに対して、チェイン法では下記のメリットがあるので、オープンアドレス法よりも探索効率は高いはずです。

• 削除済みのデータを含めずに探索できる
• 他のハッシュ値のデータを含めずに探索できる
• 次の探索先を決めるときに毎回ハッシュ値を算出する必要がない

まとめ

このページではチェイン法について解説しました！

チェイン法は、ハッシュ法で衝突が発生した際でも探索を正常に動作させるための対処法の一つで、要はハッシュ法におけるハッシュテーブルのバケットをリストとして扱う手法になります。

リストには後からデータの追加が可能ですので、衝突が発生したデータ全てをハッシュテーブル内に保持でき、探索も正常に動作させることが可能です。ただし、探索時はリストのノードを辿って探索する必要があるので注意してください。

ソースコードだけ見るとオープンアドレス法よりも複雑にも思えますが、リストを既に実装していれば、ハッシュ法の実装にその実装を組み合わせれば良いだけなのでオープンアドレス法よりも簡単に実装できます。

リストはいろんな場で利用できて便利ですので、ぜひ一度実装し、その実装を使いまわせるようにしておくことをオススメします！