【C言語】動的計画法をナップサック問題を解いて理解する

このページでは「動的計画法」について、ナップサック問題を解きながら解説していきたいと思います！

動的計画法という言葉を聞くと難しそうに思えるかもしれませんが、実は原理は非常に単純です。

個人的には、大事なのは動的計画法がどのようなものであるかを知っておくことよりも、効率よく問題を解くためにはどうすれば良いかを考えることだと思っています。特にナップサック問題においては、それを考えることで自然と動的計画法を導き出すことができます。

ですので、このページでは実際にナップサック問題を解きながら、効率よく解くための方法を考えていく形で動的計画法について解説していきたいと思います。

そしてその後、結局動的計画法がどんなアルゴリズムであるのかについてまとめていきたいと思います！

ナップサック問題を解く

ということで、まずはナップサック問題を解いていきましょう！

このナップサック問題は下記のような問題になります（ほぼ Wikipedia からの引用ですが、ところどころ言葉をいじっています）。このナップサック問題は、動的計画法の解説などを行う際にもよく用いられる問題です。

石 0 〜 石 N - 1 の N 個の候補の石（石 i の価値は value[i]、石 i の重量は weight[i]）が与えられたとき、「重量の合計がナップサックの容量 C を超えない範囲で石のいくつかをナップサックに入れ、その入れた石の価値の合計を最大化するには入れる石の組み合わせをどのように選べばよいか」という整数計画問題である。

引用元：Wikipedia

今回は、ナップサックには同じ石は入れることができないものとして、ナップサック問題を解いていきたいと思います。

例えば石の候補は 3 つとし、石 0・石 1・石 2 の価値と重量がそれぞれ下記であるとします。

• 石 0：
  • 価値 1
  • 重量 2
• 石 1：
  • 価値 2
  • 重量 2
• 石 2：
  • 価値 4
  • 重量 3

さらに、ナップサックの容量を 5 とした時、ナップサックに入れた石の価値の合計の最大値はいくつになるでしょうか？

こんな感じの問題がナップサック問題です。

今回の場合は非常に簡単で、石 1 と石 2 をナップサックに入れた時が石の価値の合計が最大値で、この最大値は 6 となります。

ただ、ナップサックに入れる石の候補数が多くなればなるほど、問題が難しくなることは容易に想像できるのではないかと思います。

ナップサック問題を小さな問題に分割して解く

では、このナップサック問題を解く関数の作り方を考えていきたいと思います。

ナップサック問題を全探索で解く

まずは全探索で問題を解くことを考えてみましょう。つまり、ナップサックに入れる石の組み合わせの全パターンを試し、その中から最大となる価値を見つけ出します。

この石の組み合わせの全パターンは、全ての候補の石に対してナップサックに「入れる or 入れない」の２パターンを試していくことで網羅することが可能です。

例えば先ほどの例の場合、ナップサック問題の各条件は以下のように設定されていました。

• ナップサックの容量 5
• 石の候補：石 0 と石 1 と石 2
  • 石 0：
    • 価値 2
    • 重量 1
  • 石 1：
    • 価値 2
    • 重量 2
  • 石 2：
    • 価値 3
    • 重量 4

まずは、この例のナップサック問題を全探索で解く方法について考えていきましょう！

簡単のため、ここからはナップサック問題を下記のような形式で表現していきたいと思います。

ナップサック(石の候補の先頭の番号, ナップサックの容量)

つまり ナップサック(i, c) は、ナップサックの容量 c を超えないように石 i から最後の候補の石（つまり石 2 ）の石をナップサックに入れた時にとりうる最大の価値を求める問題になります。

上記の問題は、石の候補の先頭が石 0 で、さらに容量 5 のナップサックに入れた時の最大価値を求めるナップサック問題ですので、ナップサック(0, 5) と表現していきます。

このナップサック問題を全探索で解く場合、下の図のように、各石を入れるパターンと入れないパターンの全ての組み合わせを作り出し、その組み合わせの中から最大の価値になるものを見つけ出せば良いことになります（石の重量がナップサックの容量を超える組み合わせに関してはバツマークを付けています）。

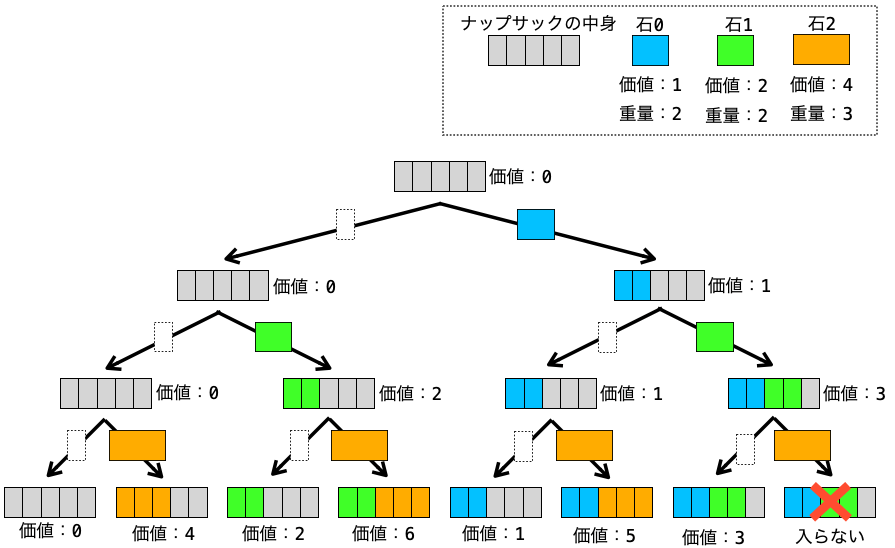
ナップサック問題を小さなナップサック問題に分割する

ナップサック問題のような目当てとなる解を全探索で見つけ出す問題は、問題を小さく分割していくことで簡単に解くことができます。

動的計画法を理解する上では、この「問題を小さな問題に分割する考え方」が重要になります。

まずは、下の図の点線で囲った部分に注目したいと思います。

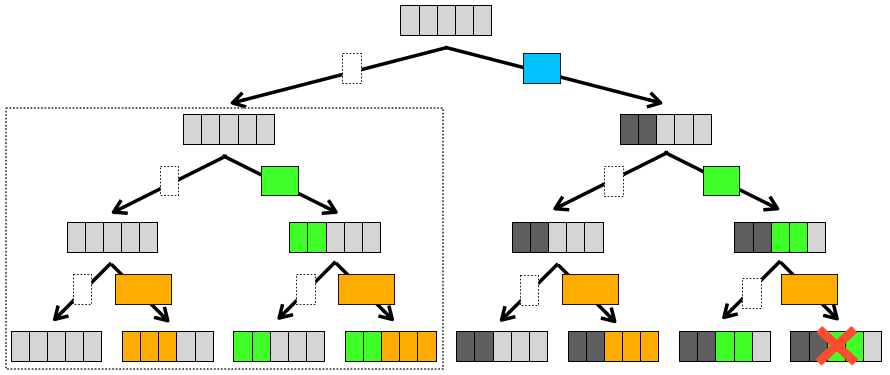
この点線で囲った部分は、「石 0 を入れない」と仮定した上で、他の石の候補（石 1 と石 2）を入れるパターンと入れないパターンの全ての組み合わせを示したものになります。

つまり、これらの組み合わせの中から価値が最大になるものを見つける問題は、下記の条件のナップサック問題を解くことと同義になります。

• ナップサックの容量 5
• 石の候補：石 1 と石 2
  • 石 1：
    • 価値 2
    • 重量 2
  • 石 2：
    • 価値 3
    • 重量 4

同じナップサック問題ではありますが、元々のナップサック問題に比べると石の候補数が減っているので、元々のナップサック問題よりも小さな問題（簡単な問題）であると考えることができます。

この問題は、石の候補の先頭が石 1 で、最大容量 5 のナップサックに入れた時の最大価値を求めるナップサック問題ですので、ナップサック(1, 5) と表現していきます。

さらに次は、下の図の点線で囲った部分に注目したいと思います。

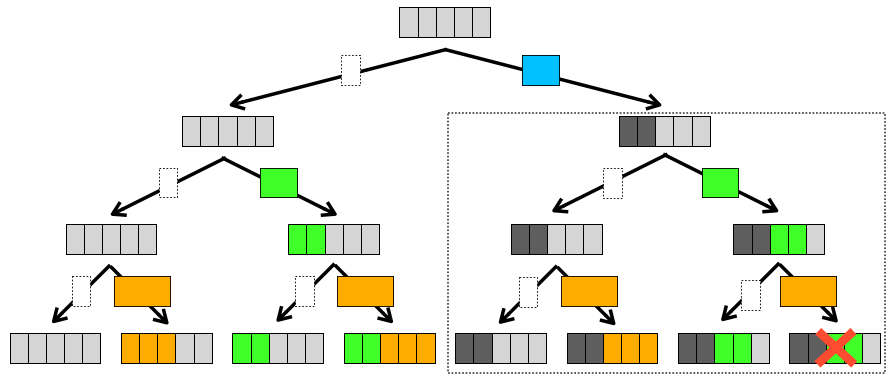
この点線で囲った部分は、「石 0 を入れる」と仮定した上で、他の石の候補（石 1 と石 2）を入れるパターンと入れないパターンの全ての組み合わせを示したものになります。

つまり、これらの組み合わせの中から価値が最大になるものを見つける問題は、下記の条件のナップサック問題を解くことと同義になります。石 0 を入れると仮定しているので、ナップサックの容量は元々の容量から石 0 の重量（つまり 2）減っています。

• ナップサックの容量 3
• 石の候補：石 1 と石 2
  • 石 1：
    • 価値 2
    • 重量 2
  • 石 2：
    • 価値 3
    • 重量 4

こちらも元々のナップサック問題に比べると、石の候補数が減っている（さらにはナップサックの容量も減っている）ので、元々のナップサック問題よりも小さな問題（簡単な問題）であると考えることができます。

この問題は、石の候補の先頭が石 1 で、最大容量 3 のナップサックに入れた時の最大価値を求めるナップサック問題ですので、ナップサック(1, 3) と表現していきます。

ナップサック問題を小さな問題の解を利用して解く

ここで、元々のナップサック問題 ナップサック(0, 5) を解くことを考えていきたいと思います。

このナップサック問題は、前述で紹介した小さく分割したナップサック問題、つまり ナップサック(1, 5) と ナップサック(1, 3) のそれぞれの解を利用して解くことができます。

順番が前後しますが、前述の通り ナップサック(1, 3) は「石 0 を入れる」と仮定した上で、他の石の候補（石 1 と石 2）を入れるパターンと入れないパターンの全ての組み合わせにおける最大価値を見つけ出すナップサック問題です。

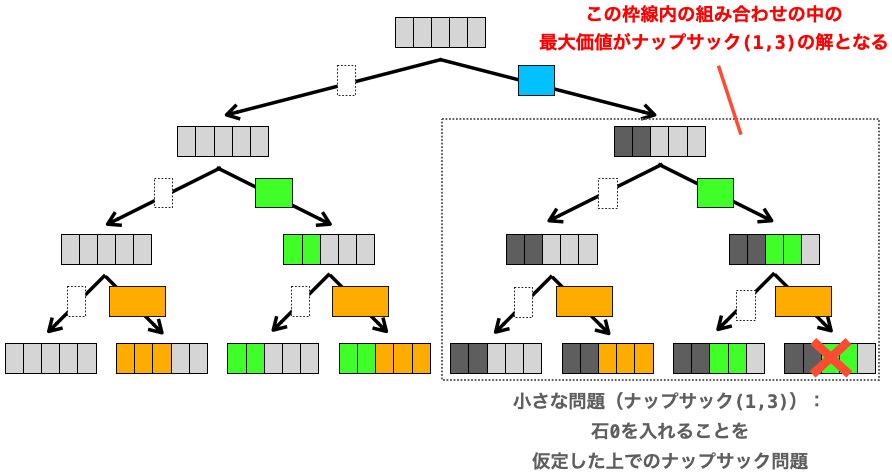
したがって、あとは石 0 を実際にナップサックに入れる試行をしてやれば、すなわち、ナップサック(1, 3) の解に石 0 の価値を足してやれば、石 0 をナップサックに入れたパターンで取りうる最大価値を算出することができます。

また、ナップサック(1, 5) は「石 0 を入れない」と仮定した上で、他の石の候補（石 1 と石 2）を入れるパターンと入れないパターンの全ての組み合わせにおける最大価値を見つけ出すナップサック問題です。

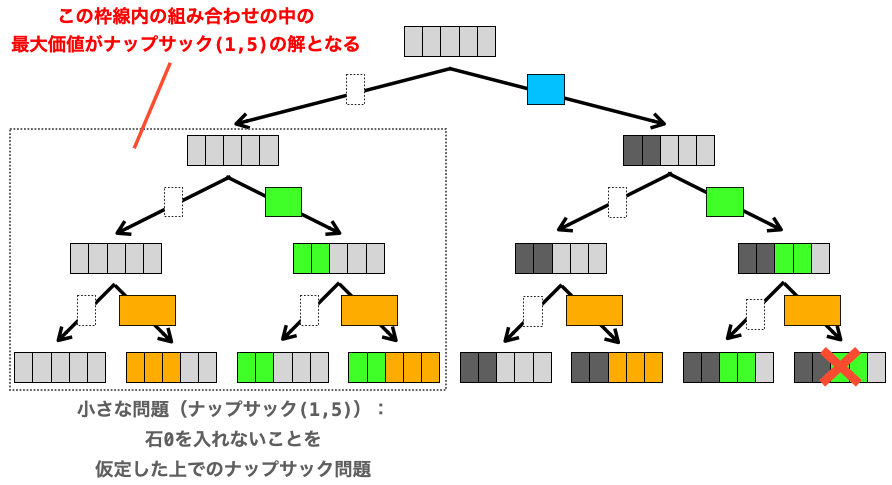
したがって、あとは石 0 を実際にナップサックに入れる試行をしてやれば、石 0 をナップサックに入れたパターンで取りうる最大価値を算出することができます。ただし、石をナップサックに入れないということは、ナップサックの中の石の価値の合計は当然変わりませんので、ナップサック(1, 5) の解そのものが、石 0 をナップサックに入れなかったパターンに取りうる最大価値となります。

つまり、ここで求めた「石 0 をナップサックに入れなかったパターンで取りうる最大価値」と「石 0 をナップサックに入れたパターンで取りうる最大価値」が ナップサック(0, 5) の解の候補であり、大きい方の値が ナップサック(0, 5) の解となります。

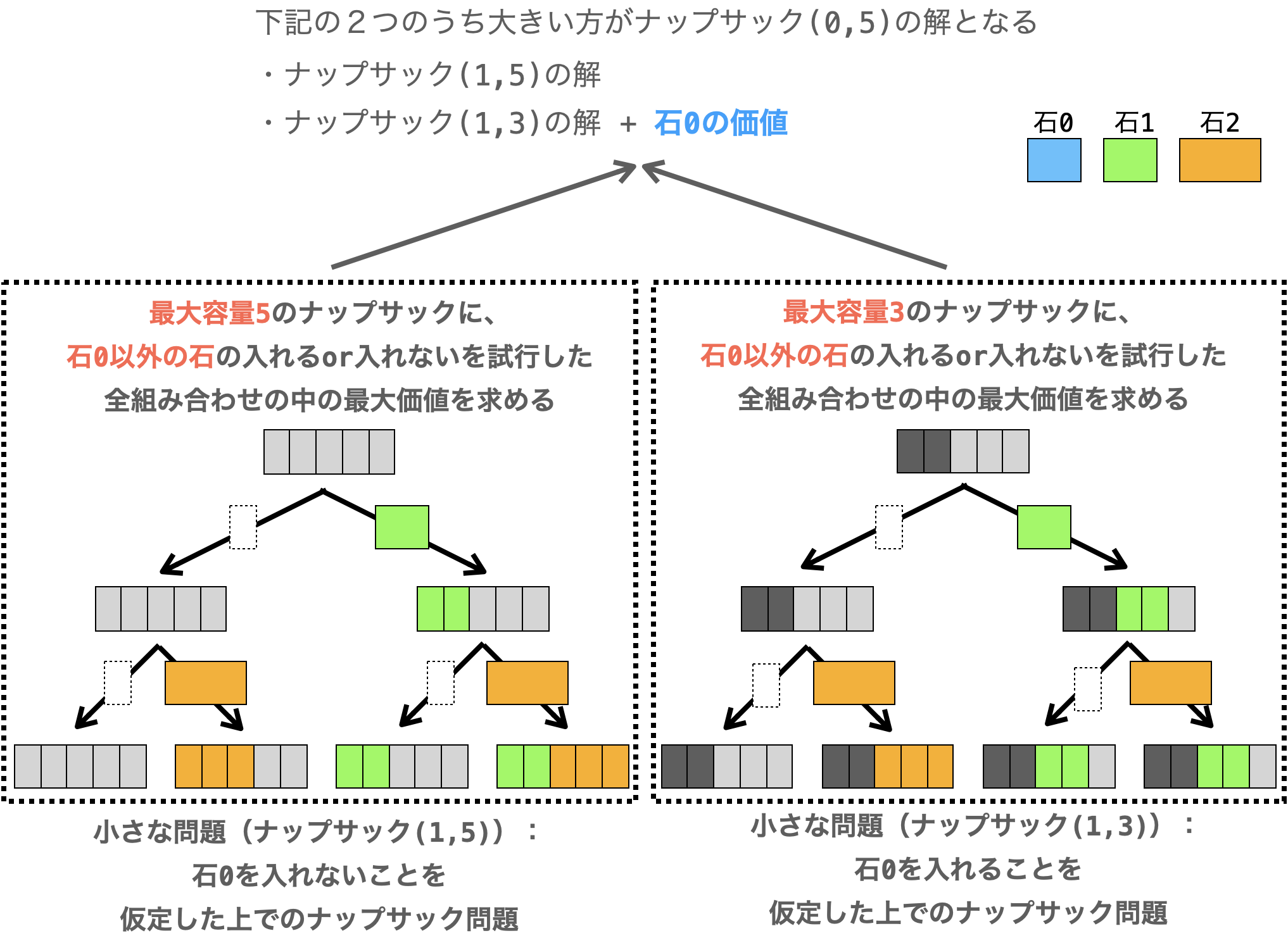
ですので、上記で求めた２つの価値の比較して大きい方の値を求めれば、その値を本ナップサック問題の解として算出することができます。

• ナップサック(0, 5)の解：
  • 下記の大きい方の値
    • ナップサック(1, 5) の解
    • ナップサック(1, 5 - 石 0 の重量) の解 + 石 0 の価値
      • （ナップサック(1, 5 - 石 0 の重量) = ナップサック(1, 3)）

ここでのポイントは、大きなナップサック問題は、その問題を小さく分割したナップサック問題の解から簡単に求めることができるというところになります。

では、ナップサック(1, 5) や ナップサック(1, 3) はどうやって解けば良いのかというと、これも同じ考えで問題をさらに小さく分割していくことで解くことができます。

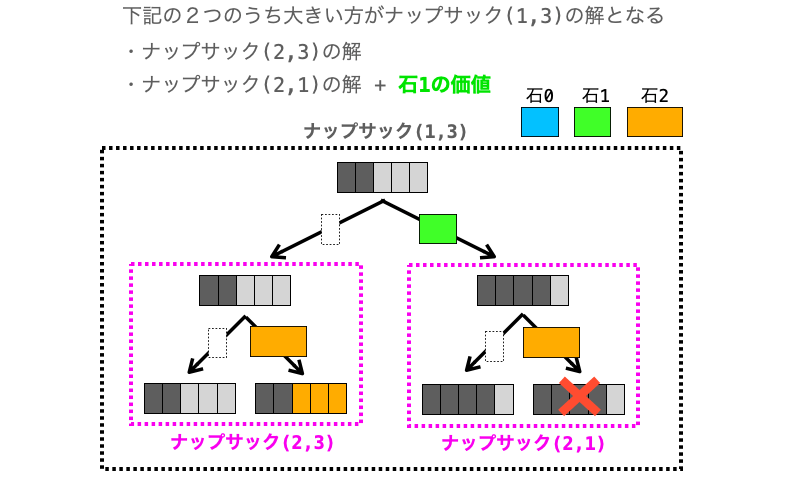
例えば上の図のように ナップサック(1, 3) を解くのであれば、今度は「石 1 を入れない」と仮定することで小さく分割されたナップサック問題 ナップサック(2, 3) と「石 1 を入れる」と仮定することで小さく分割されたナップサック問題 ナップサック(2, 1) とを解き、先ほどと同様に最大価値の比較を行うことで解くことができます（石 1 の重量は 2 なので、石 1 を入れると仮定する場合はナップサックの最大容量が 2 減る）。

• ナップサック(1, 3)の解：
  • 下記の大きい方の値
    • ナップサック(2, 3) の解
    • ナップサック(2, 3 - 石 1 の重量) の解 + 石 1 の価値
      • （ナップサック(2, 3 - 石 1 の重量) = ナップサック(2, 1)）

当然ここで出てくる ナップサック(2, 3) や ナップサック(2, 1) に関しても、さらにナップサック問題を小さく分割していくことで解くことができます。

元々の大きな問題であっても、分割して小さくしたナップサック問題であっても、結局は “ナップサックに入れる候補の先頭の石を「入れる or 入れない」で仮定した時の２つのナップサック問題の解” から解を求めることができます。

つまり、ナップサックに入れる石の候補の先頭が石 i、ナップサックの容量が c であるナップサック問題 ナップサック(i, c) は、下記により解くことができます。

• ナップサック(i, c)の解：
  • 下記の大きい方の値
    • ナップサック(i + 1, c) の解
    • ナップサック(i + 1, c - 石 i の重量) の解 + 石 i の価値

このように大きな問題を小さな問題に分割し、その小さな問題の解を利用して大きな問題を解くような解決手法を “分割統治法” と呼びます。

ここまでは、解きたいナップサック問題におけるナップサックに入れる石の候補数を 3、ナップサックの容量を 5 として考えてきましたが、上記によりナップサック問題が解けるのはこの場合だけでなく、石の候補数やナップサックの容量が正の整数であればどんな問題でも解くことができます。

ですので、ここからはナップサックに入れる石の候補数は N、ナップサックの容量は C として説明していきたいと思います。

ナップサック問題を全探索で解く関数

前述の通り、ナップサック問題は下記により、全探索で解くことができます。次はこの ナップサック を解く関数を作成していきたいと思います。

• ナップサック(i, c) の解：
  • 下記の大きい方の値
    • ナップサック(i + 1, c) の解
    • ナップサック(i + 1, c - 石 i の重量) の解 + 石 i の価値

ナップサック問題 ナップサック を解く関数の名前を knapsack とすれば（返却値をナップサック問題の解とする）、問題 ナップサック(i, c) を解く場合 knapsack(i, c) を実行すれば良いことになります。

さらに上記より、knapsack(i, c) では次の２つのうちの大きい方を返却すれば良いことになります。

• knapsack(i + 1, c) の返却値
• knapsack(i + 1, c - 石 i の重量) の返却値 + 石 i の価値

したがって ナップサック を解く関数は、下記の knapsack.c における knapsack 関数のように再帰関数として記述することができます。

weight[i] は石 i の重量、value[i] は石 i の価値、N はナップサックに入れる石の候補数、C はナップサックの容量としています。

#include <stdio.h>

#define N 10
#define C 40

int weight[N] = {
    2, 2, 3, 4, 5, 6, 7, 8, 9, 9,
};

int value[N] =  {
    3, 2, 3, 6, 7, 8, 6, 8, 8, 9,
};

/************************************
 * 石iから石N-1を入れた時の最大価値を求める
 * i：最初に入れるor入れないを試行する石の番号
 * c：ナップサックの空き容量
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack(int i, int c) {
    int put_value;
    int no_put_value;
    int max_value;

    if (i > N - 1) {
        /* もう入れる石がない */
        return 0;
    }

    /* 石iを入れなかった場合の最大価値を求める */
    no_put_value = knapsack(i + 1, c);
    
    /* 石iがナップサックに入る場合だけ石を入れる */
    if (weight[i] <= c) {
        /* 石iがまだナップサックに入る場合 */

        /* 石iを入れた場合の最大価値を求める */
        /* 石iを入れるのでナップサックの容量cはweight[i]減る */
        /* 石iを入れるので価値はvalue[i]増える */
        put_value = knapsack(i + 1, c - weight[i]) + value[i];
    } else {
        /* もう石iがナップサックに入らない場合 */

        /* 価値は-1としておく(no_put_valueよりも必ず小さい値) */
        put_value = -1;
    }
    
    /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    return max_value;
}

int main(void) {
    int ret;

    /* 石の候補数N、ナップサックの容量Cの
       ナップサック問題を解く */
    ret = knapsack(0, C);

    /* 解いたナップサック問題の解を表示 */
    printf("%d\n", ret);

    return 0;
}

knapsack.c では、main 関数から knapsack(0, C) を実行することで、石の候補数が N かつナップサックの容量が C のナップサック問題を解いています（さらに N 個の石の重量が weight、価値が value として与えられている）。

N、C、weight、value を変更することで、いろんなパラメータのナップサック問題を解くことができます。 

さて、先程紹介した knapsack 関数の説明に戻ると、この関数は自分自身である knapsack 関数を呼び出しているので再帰関数となります。

第１引数である石の候補の先頭の番号 i を +1 してから knapsack 関数を再帰呼び出ししているので、どんどん小さなナップサック問題に分割しながら処理が進んでいくことになります（引数 i が大きいほど問題が小さくなることに注意してください。引数 i が大きいほど石の候補数が減るので、問題が小さくなったことになります）。

また、i は次にナップサックに「入れる or 入れない」を試行する石の番号であり、N - 1 は候補の最後の石の番号です。ですので、i が N - 1 よりも大きくなった場合は、もうナップサックに「入れる or 入れない」を試行する石が存在しないことになります。

したがって、この場合の解は必ず 0 になります。つまり、解が自明になるまで問題を小さくできたことになります。

解が自明になるまで問題を小さくできているのであれば、それ以上問題を小さくする必要はありません。ですので、それ以降は knapsack 関数の再帰呼び出しは行わず、単に 0 を返却して即座に関数を終了するようにしています。

また、weight[i] > c の場合は石 i をナップサックに入れると容量を超えてしまうことになるため、この場合は knapsack(i + 1, c - weight[i]) を呼び出さず返却値は必ず knapsack(i + 1, c) の値となるようにしています。

この knapsack 関数のポイントは、より小さなナップサック問題を解く knapsack(i + 1, c) と knapsack(i + 1, c - weight[i]) の解を利用して大きなナップサック問題を解いているところです。

ここから説明していく動的計画法は、この小さな問題の解から大きな問題を解くことができることを利用したアルゴリズムになります。

というか、上記 knapsack 関数のような、小さな問題の解から大きな問題を解く構造の関数さえ作成してしまえば、後な簡単に動的計画法を適用した関数に変形していくことができます。

スポンサーリンク

トップダウン方式の動的計画法でナップサック問題を解く

先程紹介した knapsack 関数は全探索（正確にはナップサックの容量を超えた場合の組み合わせは調べないので “ほぼ” 全探索）でナップサック問題を解く関数になります。

この全探索でナップサック問題を解く場合、石の候補数を N とすれば、解を求めるのに必要な計算量のオーダーは O(2^N) となります（2^N は 2 の N 乗を表しています）。

N に関して指数関数的に計算量が増えることになりますので、全探索では N が大きいと解を求めるのが難しくなります（私の環境だと N = 50 になるともう解けないですね…）。

では次は、この全探索における計算量を減らす方法について考えていきましょう！その方法の考え方が動的計画法になります！

ナップサック問題では同じ小さな問題を何回も解いている

ここで、最初にも紹介した下記の条件のナップサック問題について解くことを考えていきたいと思います

• ナップサックの容量 5
• 石の候補：石 0 と石 1 と石 2
  • 石 0：
    • 価値 2
    • 重量 2
  • 石 1：
    • 価値 4
    • 重量 2
  • 石 2：
    • 価値 3
    • 重量 3

上記のナップサック問題は、knapsack 関数を利用すれば knapsack(0, 5) を実行することで解くことができます。

この knapsack 関数の中では knapsack 関数を再帰呼び出ししていますので、引数を変更しながらどんどん knapsack 関数が実行されていきます。

その knapsack 関数の呼び出しの流れを図示したのが下記になります（knapsack(3, x) に関しては、もう試行する石が残っていないので必ず 0 が返却され、それ以降 knapsack 関数が呼ばれることはありません）。

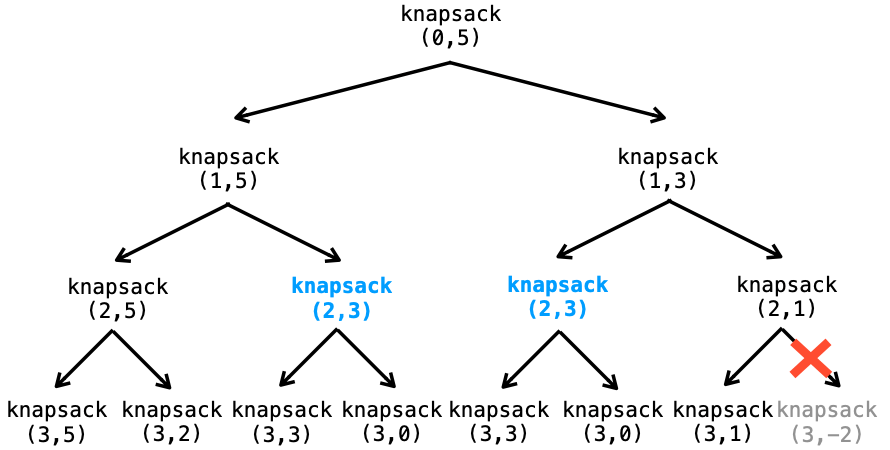
ここで注目していただきたいのが、青字で示した２つの knapsack 関数の呼び出し部分です（knapsack(2, 3)）。この２つは全く同じ引数で knapsack 関数が呼び出されていることになります。

さらに、knapsack 関数の処理を確認してみると、引数 i と引数 c が同じであれば同じ返却値になることが確認出来ます（ナップサック問題では、問題を解く途中で石の重量 weight や石の価値 value は変化しない）。

なのであれば、同じ引数の knapsack 関数を毎回実行するのはもったいないですね！そして、この引数が同じ場合の knapsack の実行をしなくても良いようにすれば、ナップサック問題を効率的に解くことができそうです。

メモを利用して同じ問題を解くことを避ける

では、どうすれば同じ引数の knapsack 関数を実行しなくても済むようになるでしょうか？

これは、あなたが同じ問題を何回も解く場合に、どうやって効率よく問題を解くかを考えれば簡単に方法を導き出せると思います。

例えば下記の５つの問題を解く場合、あなたはどうやって問題を解いていきますか？

1. 99 + 257
2. 45 + 896
3. 99 + 257
4. 45 + 896
5. 99 + 257

おそらくほぼ全ての人は、1. と 2. に関しては普通に計算して問題を解いて答えをメモしておき（覚えておき）、3. と 5. に関しては 1. の答えを、4. に関しては 2. の答えを使い回すことで解くのではないかと思います。

こうすれば、3. と 4. と 5. に関しては計算しなくて済むので効率的に問題を解くことができます。

ナップサック問題の場合もこれと一緒で、knapsack 関数の実行結果（返却値）をメモしておき、それを使い回すようにすることで、同じ引数の knapsack 関数を実行しなくても済むようになります。

例えば、関数の実行結果をメモする配列の名前を memo とすれば、knapsack(i, c) の実行結果を memo[i][[c]] に格納していく感じですね。実行結果とはすなわち返却値なので、return で値を返却する前に、その返却値を配列に格納するようにしていきます。

引数を添字とする位置に実行結果を格納するようにしているのは、以降で引数からその実行結果を簡単に参照できるようにするためです。

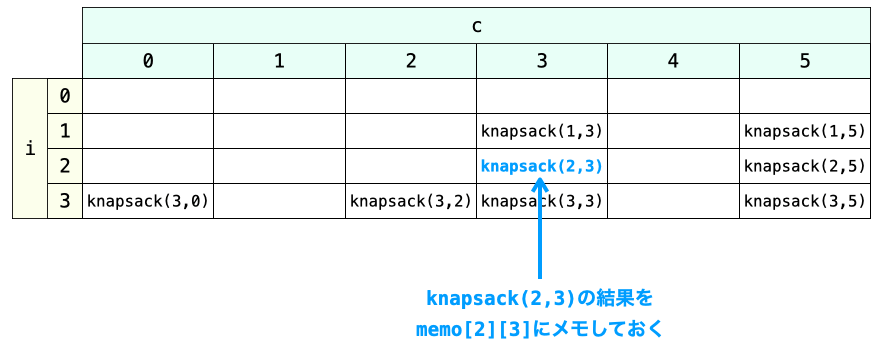
さらに、knapsack 関数の先頭で、配列の引数を添字とする位置に以前実行した結果がメモされているかどうかを確認するようにします。

もしメモされているのであれば、それ以降の再帰呼び出しは行わず、そのメモされた結果の返却のみを行うようにします（メモされていない場合は、通常通り再帰呼び出しを行ない、関数終了時に memo にメモを残す）。

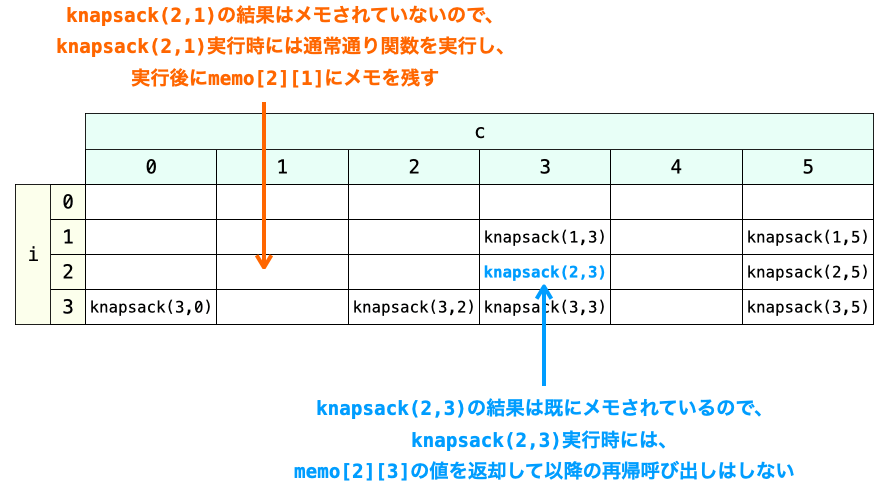
以上のようにメモを利用することで、knapsack 関数が同じ引数で何回も実行された場合、２回目以降は knapsack 関数の再帰呼び出しをスキップすることができ、同じ処理を繰り返すことを避けることができるようになります。

また、石の候補数が N でナップサックの容量が C のようなナップサック問題を knapsack 関数で解く場合（つまり knapsack(0, C) を実行する場合）、引数 i と c がとりうる値はそれぞれ 0 〜 N と 0 〜 C となります（これは knapsack 関数の処理から確認できると思います）。

メモは、これらの引数それぞれを区別できるように配列に記憶する必要があるため、配列のサイズは (N + 1) * (C + 1) 必要になります。 

ここで、このメモの利用について補足しておきます。

knapsack 関数は同じ引数で実行した場合には必ず同じ結果になりますが、全ての再帰関数がそうであるとは限らないので注意してください。

例えば再帰関数の実行結果がグローバル変数の値から決まる＆再帰関数の中でグローバル変数の値を変更するような場合、同じ引数であっても同じ結果にはならなくなります。

このような場合は、そのグローバル変数の値も区別できるようにメモを取る必要があります。例えばそのグローバル変数の変数名が g であり、さらに再帰関数の実行結果が引数 i と引数 c と引数 g によって決まるのであれば、memo[i][[c]][g] にメモをとるようにする必要があります。さらに、このようにメモを取るためには、配列 memo のサイズを下記のように設定する必要があります。

int memo[iが取りうる値のパターン数][cが取りうる値のパターン数][gが取りうる値のパターン数];

つまり、”関数の実行結果に影響を与える＆関数実行時に変化する” 要因全てを区別してメモを取れるようにする必要があります。

これらの要因が多いと配列のサイズが巨大になってメモリ不足でプログラムが動作しなくなるので注意してください。

トップダウン方式の動的計画法でナップサック問題を解く関数

メモを利用するように knapsack 関数を変更したものが、下記の knapsack_memo.c における knapsack_memo 関数となります（knapsack_memo 関数は、memo の全要素に -1 が格納されていることを前提とした作りになっているので注意してください）。

#include <stdio.h>

#define N 10
#define C 40

int weight[N] = {
    2, 2, 3, 4, 5, 6, 7, 8, 9, 9,
};

int value[N] =  {
    3, 2, 3, 6, 7, 8, 6, 8, 8, 9,
};

/* knapsack_memoの実行結果を格納する配列 */
int memo[N + 1][C + 1];

/************************************
 * 石iから石n-1を入れた時の最大価値を求める
 * i：最初に入れるor入れないを試行する石の番号
 * c：ナップサックの空き容量
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack_memo(int i, int c) {
    int put_value;
    int no_put_value;
    int max_value;

    if (memo[i][c] != -1) {
        /* この引数での関数結果はメモずみ */
 
        return memo[i][c];
    }

    if (i > N - 1) {
        /* もう入れる石がない */

        /* 関数の実行結果をメモ */
        memo[i][c] = 0;
        return 0;
    }

    /* 石iを入れなかった場合の最大価値を求める */
    no_put_value = knapsack_memo(i + 1, c);
    
    /* 石iがナップサックに入る場合だけ石を入れる */
    if (weight[i] <= c) {
        /* 石iがまだナップサックに入る場合 */

        /* 石iを入れた場合の最大価値を求める */
        /* 石iを入れるのでcはweight[i]減る */
        /* 石iを入れるので価値はvalue[i]増える */
        put_value = knapsack_memo(i + 1, c - weight[i]) + value[i];
    } else {
        /* もう石iがナップサックに入らない場合 */

        /* 価値は-1としておく(no_put_valueよりも必ず小さい値) */
        put_value = -1;
    }
    
    /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    /* 関数の実行結果をメモ */
    memo[i][c] = max_value;

    return max_value;
}

int main(void) {
    int ret;
    int i, c;

    /* メモを記録する配列を初期化 */
    for (i = 0; i < N + 1; i++) {
        for (c = 0; c < C + 1; c++) {
            memo[i][c] = -1;
        }
    }

    /* 石の候補数N、ナップサックの容量Cの
       ナップサック問題を解く */
    ret = knapsack_memo(0, C);

    /* 解いたナップサック問題の解を表示 */
    printf("%d\n", ret);

    return 0;
}

上記では、main 関数から knapsack_memo(0, C) を実行することで、石の候補数が N かつナップサックの容量が C のナップサック問題を解いています。

メモする値は knapsack_memo 関数の実行結果、すなわち knapsack_memo 関数が return する値ですので、return 直前でその返却値を memo[i][[c]] にメモするようにしています。

/* 関数の実行結果をメモ */
memo[i][c] = 0;
return 0;

/* 関数の実行結果をメモ */
memo[i][c] = max_value;
return max_value;

さらに knapsack_memo 関数の先頭付近の下記部分は、すで配列 memo に関数実行結果がメモされている場合の処理になります。この場合は、関数を実行しなくても memo[i][[c]] に結果がメモされているのですから、以降の処理は行わずに関数実行結果である memo[i][[c]] の返却のみを行うようにしています。

if (memo[i][c] != -1) {
    /* この引数での関数結果はメモずみ */

    return memo[i][c];
}

この節の最初にも紹介した下図の knapsack 関数の呼び出し関係だけをみるとあまり効果はなさそうに見えますが、これは石の候補数 N が少ないからです。

この石の候補数 N を増やせば増やすほど、同じ引数として実行される箇所が多くなりますので、その分処理効率を向上させることができます。

例えば N と C と weightと value を下記のように設定した場合、

#define N 30
#define C 100

int weight[N] = {
    2, 2, 3, 4, 5, 6, 7, 8, 9, 9,
    5, 8, 9, 7, 2, 1, 5, 4, 3, 8,
    1, 5, 4, 8, 6, 3, 2, 1, 9, 4
};

int value[N] =  {
    3, 2, 3, 6, 7, 8, 6, 8, 8, 9,
    5, 4, 1, 5, 9, 8, 5, 3, 2, 8,
    9, 1, 5, 4, 7, 9, 1, 5, 4, 8
};

knapsack 関数で解を求めるまでにかかる時間と knapsack_memo 関数で解を求めるまでにかかる時間は下記のようになりました。

knapsack関数：11.350932
knapsack_memo関数：0.000048

圧倒的に knapsack_memo 関数の方が処理が速いことが確認できると思います。ちなみに、knapsack 関数と knapsack_memo 関数それぞれが実行される回数は下記のようになりました。

knapsack関数：2067662480回
knapsack_memo関数：3909回

この結果から、knapsack 関数の中で行われる再帰呼び出しの中の９９％以上は同じ引数で実行されている（同じ問題が解かれている）ことが分かります。

それらの同じ引数で実行される関数の実行がメモによってスキップされるようになるわけですから、ナップサック問題を解く上でメモを取る効果が高いという点を実感していただけるのではないかと思います。

このメモをとって処理を効率化する方法において重要なのが、ナップサック問題を小さな問題に分割して解く で解説した「大きな問題の小さな問題への分割」です。

大きな問題単位で考えると同じ処理を何回も実行していることに気づきにくいですが、小さな問題に分割してやることで、大きな問題を解くために同じ小さな問題が何回も解かれていることが浮き彫りになってきます。

そうなれば、後は同じ小さな問題が何回も繰り返されることを避けるための対処（メモの利用）をすれば良いだけになります。

ただ、小さな問題への分割の仕方によって、メモの効果が薄れるようなケースもあります。これについては後述で解説します。

このように、大きな問題を小さな問題に分割し、その小さな問題の解を記録しておくことで同じ処理を繰り返すことを避けるのが「動的計画法」になります。

要は、全探索を行う再帰関数を作れば、あとは関数の実行結果をメモするようすれば良いだけなので、実現はかなり簡単だと思います。

また、同じ処理が繰り返し行われなくなるので処理が高速になることも直感的に理解していただけるのではないかと思います。

特に今回作成した knapsack_memo のように、再帰呼び出しの中で上記を実現する手法を「メモ化再帰」と呼びます。

さらに上記の knapsack_memo.c では、main 関数から knapsack_memo(0, C) を実行しているので、解きたい問題（一番大きな問題）を解くことを最初に試みていることになります。

このように、大きな問題（解きたい問題）から順に問題を解くことを試みる場合の動的計画法を「トップダウン方式の動的計画法」と呼んだりもします。

逆に、小さな問題から順に問題を解いていくことで動的計画法を実現することをボトムアップ方式の動的計画法と呼びます。次は、ナップサック問題をこのボトムアップ方式の動的計画法を解説していきたいと思います。

ボトムアップ方式の動的計画法でナップサック問題を解く

では、次はもうちょっと違うやり方でナップサック問題を解くことを考えていきたいと思います。

小さな問題から解いていけば再帰呼び出しは不要

まずは先程紹介した knapsack_memo.c における knapsack_memo 関数を変形して作成した下記の関数について考えてみたいと思います。

int memo[N + 1][C + 1];

/************************************
 * 石iから石N-1を入れた時の最大価値を求める
 * i：最初に入れることを試行する石の番号
 * c：ナップサックの空き容量
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack_memo_kai(int i, int c) {
    int put_value;
    int no_put_value;
    int max_value;

    if (i > N - 1) {
        /* もう入れる石がない */

        memo[i][c] = 0;
        return 0;
    }

    /* 石iを入れなかった場合の最大価値を求める */
    if (memo[i + 1][c] != -1) {
        no_put_value = memo[i + 1][c];
    } else {
        no_put_value = knapsack_memo_kai(i + 1, c);
    }

    /* 石iがナップサックに入る場合だけ石を入れる */
    if (weight[i] <= c) {
        /* 石iがまだナップサックに入る場合 */
        if (memo[i + 1][c - weight[i]] != -1) {
            put_value = memo[i + 1][c - weight[i]] + value[i];
        } else {
            /* 石iを入れた場合の最大価値を求める */
            /* 石iを入れるのでcはweight[i]減る */
            /* 石iを入れるので価値はvalue[i]増える */
            put_value = knapsack_memo_kai(i + 1, c - weight[i]) + value[i];
        }
    } else {
        /* もう石iがナップサックに入らない場合 */

        /* 価値は-1としておく(no_put_valueよりも必ず小さい値) */
        put_value = -1;
    }
    
    /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    /* 関数の実行結果をメモ */
    memo[i][c] = max_value;

    return max_value;
}

上記の knapsack_memo_kai は knapsack_memo と同じ結果を得ることができる関数です。違いは下記になります。

• knapsack_memo_kai：再帰呼び出しする前にメモしているかを確認する
• knapsack_memo：再帰呼び出しされた後にメモしているかを確認する

なぜ knapsack_memo_kai をわざわざ用意したかというと、knapsack_memo_kai の方が、ナップサック問題を解く時、どんなケースで再帰呼び出しが必要になるかが分かりやすくなるからです。

で、この答えが knapsack_memo_kai 関数の下記の部分になります（コメントは省略しています）。

if (memo[i + 1][c] != -1) {
    no_put_value = memo[i + 1][c];
} else {
    no_put_value = knapsack_memo_kai(i + 1, c);
}

if (memo[i + 1][c - weight[i]] != -1) {
    put_value = memo[i + 1][c - weight[i]] + value[i];
} else {
    put_value = knapsack_memo_kai(i + 1, c - weight[i]) + value[i];
}

つまり、knapsack_memo_kai(i, c) 実行時に再帰呼び出しが必要になるケースは memo[i + 1][[c]] と memo[i + 1][[c - weight[i]]] にまだメモが残されていない場合です。

要は、解こうとしている問題を解くためには、そこから分割した小さな問題の答え（より i が大きい階層の問題の答え）のメモがないと、再帰呼び出しを行わなくてはならないということです。

逆に考えれば、小さな問題から先に解いてメモを残しておけば、問題を解くのに再帰呼び出しは不要であるとも言えます。

今回のナップサック問題の場合、ナップサック問題を小さな問題に分割して解く で関数の第１引数 i が大きいほど問題が小さくなるように設計しています（i が大きいほどナップサックに入れる候補の石の数が減る）。

さらに、一番小さな問題となるのは関数の第１引数 i が N の時です。この時はもうナップサックに入れる候補の石がないので必ずナップサック問題の解は 0 になります。

つまり、i = N から順に i = 0 になるまで問題を解くようにすれば（つまり knapsack_memo_kai を実行するようにすれば）、再帰呼び出しを行わずともナップサック問題を解くことができることになります。

ボトムアップ方式の動的計画法でナップサック問題を解く関数

小さな問題から問題を解いていくように knapsack_memo_kai を実行する関数が、下記の knapsack_bottom_up.c における  knapsack_bottom_up 関数になります。

#include <stdio.h>

#define N 10
#define C 40

int weight[N] = {
    2, 2, 3, 4, 5, 6, 7, 8, 9, 9,
};

int value[N] =  {
    3, 2, 3, 6, 7, 8, 6, 8, 8, 9,
};

/* knapsack_memoの実行結果を格納する配列 */
int memo[N + 1][C + 1];

/************************************
 * 石iから石n-1を入れた時の最大価値を求める
 * i：最初に入れるor入れないを試行する石の番号
 * c：ナップサックの空き容量
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack_memo_kai(int i, int c) {
    int put_value;
    int no_put_value;
    int max_value;

    if (i > N - 1) {
        /* もう入れる石がない */

        memo[i][c] = 0;
        return 0;
    }

    /* 石iを入れなかった場合の最大価値を求める */
    if (memo[i + 1][c] != -1) {
        no_put_value = memo[i + 1][c];
    } else {
        no_put_value = knapsack_memo_kai(i + 1, c);
    }

    /* 石iがナップサックに入る場合だけ石を入れる */
    if (weight[i] <= c) {
        /* 石iがまだナップサックに入る場合 */
        if (memo[i + 1][c - weight[i]] != -1) {
            put_value = memo[i + 1][c - weight[i]] + value[i];
        } else {
            /* 石iを入れた場合の最大価値を求める */
            /* 石iを入れるのでcはweight[i]減る */
            /* 石iを入れるので価値はvalue[i]増える */
            put_value = knapsack_memo_kai(i + 1, c - weight[i]) + value[i];
        }
    } else {
        /* もう石iがナップサックに入らない場合 */

        /* 価値は-1としておく(no_put_valueよりも必ず小さい値) */
        put_value = -1;
    }
    
    /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    /* 関数の実行結果をメモ */
    memo[i][c] = max_value;

    return max_value;
}

/************************************
 * 石の候補数N、ナップサックの容量Cの時のナップサック問題を解く
 * 戻り値：石の候補数N、ナップサックの容量Cの時の解
 ************************************/
int knapsack_bottom_up(void) {
    int i, c;

    /* 小さな問題（iが大きい場合）から順に問題を解いていく */
    for (i = N; i >= 0; i--) {
        for (c = 0; c <= C; c++) {
            /* 石の候補i〜N-1、ナップサックの容量cの
               ナップサック問題を解く */
            knapsack_memo_kai(i, c);
        }
    }

    /* 石の候補0〜N-1、ナップサック容量Cとした時の
       ナップサック問題の解を返却 */
    return memo[0][C];
}

int main(void) {
    int ret;
    int i, c;

    /* メモを記録する配列を初期化 */
    for (i = 0; i < N + 1; i++) {
        for (c = 0; c < C + 1; c++) {
            memo[i][c] = -1;
        }
    }

    ret = knapsack_bottom_up();

    /* 石の候補数N、ナップサックの容量Cの
       ナップサック問題の解を表示 */
    printf("%d\n", memo[0][C]);

    return 0;
}

knapsack_bottom_up 関数の中では knapsack_memo_kai(i, c) を実行しており、この knapsack_memo_kai の関数内で memo[i][[c]] にメモを残す処理が行われます。

前述の通り、knapsack_memo_kai(i, c) で必要になるメモは memo[i + 1][[c]] と memo[i + 1][[c - weight[i]]] です。

ですが、実際に c や c - weight[i] がどんな値になるかが分からない（計算すれば分かりそうだけど、それはそれで手間がかかる）ので、第２引数 c に関しては c のとりうる値（0 〜 C）全てに対して knapsack_memo_kai を実行するようにしています。

上記の knapsack_bottom_up 関数では、小さな問題から解くようにループを組んでいるので（i が大きな値から小さな値に変化するようにしている）、knapsack_memo_kai の中では下記部分で if の判断が必ず YES となり、再帰呼び出しを行わずに解を算出できるようになっています（これは再帰呼び出しをする箇所に printf を仕込んだり、ブレークポイントを貼ったりすれば確認できると思います）。

if (memo[i + 1][c] != -1) {
    no_put_value = memo[i + 1][c];
} else {
    no_put_value = knapsack_memo_kai(i + 1, c);
}

if (memo[i + 1][c - weight[i]] != -1) {
    put_value = memo[i + 1][c - weight[i]] + value[i];
} else {
    put_value = knapsack_memo_kai(i + 1, c - weight[i]) + value[i];
}

また、今回は knapsack_memo_kai(0, C) を実行した時の結果を最終的な結果とするため、その結果のメモ結果である memo[0][C] を返却しています。

上記の knapsack_bottom_up においても、大きな問題を小さな問題に分割し、その小さな問題の解を記録しておくことで同じ処理を繰り返すことを避けているので、「動的計画法」によって解を求めているということができます。

この knapsack_bottom_up のポイントは問題を解く順番（関数を実行する順番）です。

この knapsack_bottom_up においては、トップダウン方式の動的計画法でナップサック問題を解く で紹介したソースコードとは異なり、小さな問題から順に解いていって最後に一番大きな問題（解きたい問題）を解く流れになっています。

このように、小さな問題から順に解いていくことで実現する動的計画法を、ボトムアップ方式の動的計画法と呼びます。

knapsack_bottom_up 関数を見れば分かるように、knapsack_memo_kai は (N + 1) * (C + 1) 回のループの中で実行され（N：ナップサックに入れる石の候補数、C：ナップサックの容量）、さらに knapsack_memo_kai の内部では再帰呼び出しを行わないので、結局は knapsack_memo_kai の実行回数は (N + 1) * (C + 1) 回であり、計算量のオーダーは O(NC) となります。

ボトムアップ方式とトップダウン方式の違いは問題を解く順序だけ

ちなみに、上記の knapsack_bottom_up 関数では、ループの中で knapsack_memo_kai を実行していますが、変形前の knapsack_memo でも同じ処理結果が得られますし、問題を解く順番は変わらないので、これもボトムアップ方式の動的計画法による解法であるといえます。

knapsack_memo 関数の場合は、knapsack_memo 関数の再帰呼び出しが行われますが、１回目の再帰呼び出し直後の下記部分で memo[i][[c]] != -1 が成立して必ず return されことになるので、knapsack_memo_kai とそこまで処理時間も変わりません（関数呼び出しの負荷がかかるくらいで、計算量のオーダーは同じ）。

if (memo[i][c] != -1) {
    /* この引数での関数結果はメモずみ */
 
    return memo[i][c];
}

つまりですね…、ボトムアップ方式であっても、トップダウン方式であっても、実行する関数は結局は同じ “メモを行う再帰関数” であると言えます。

違うのは実行する順番だけです。

大きな問題側から実行するか（knapsack_memo(0, C) を最初に実行）、小さな問題側から実行するか（knapsack_memo(N, C) 〜 knapsack_memo(N, C) を最初に実行する）の違いだけです。

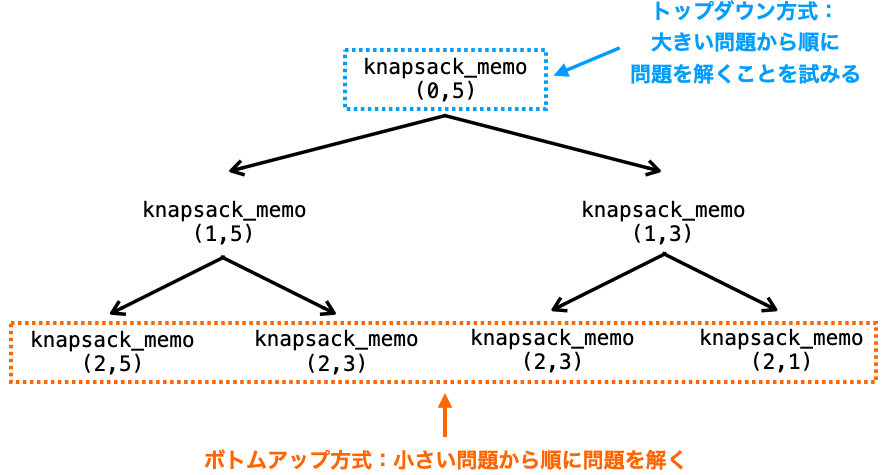
つまり、実行する順番が違うだけなので、トップダウン方式とボトムアップ方式の一方が実現できれば他方も簡単に実現することが可能です。

ボトムアップ方式の動的計画法は漸化式から導ける

ただ、ここまでの解説だと、トップダウン方式の場合は再帰関数の実行結果のメモを取るようにすれば良いだけなのに、ボトムアップ方式の場合はそれに加えてさらに再帰関数（メモを行う再帰関数）の実行順序の変更まで行わなければならないので、なんだか手間が多い気がしますよね…。

実は、ある式さえ用意できれば、ボトムアップ方式の場合は再帰関数を作らなくてもいきなり動的計画法で問題を解くことができます。

これを説明するために、ここで再度 knapsack_memo_kai について考えたいと思います。前述の通り、この knapsack_memo_kai は「小さな問題から解く」ことを前提とすれば、再帰呼び出しが行われることはありません。

ですので、この前提の元で使用される場合は、knapsack_memo_kai は下記のように変形することが可能です（変形後であっても knapsack_bottom_up で得られる結果に変わりはありません）。

/************************************
 * 石iから石n-1を入れた時の最大価値を求める
 * i：最初に入れるor入れないを試行する石の番号
 * c：ナップサックの空き容量
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack_memo_kai(int i, int c) {
    int put_value;
    int no_put_value;
    int max_value;

    if (i > N - 1) {
        /* もう入れる石がない */

        memo[i][c] = 0;
        return 0;
    }

    /* 石iを入れなかった場合の最大価値を求める */
    no_put_value = memo[i + 1][c];


    /* 石iがナップサックに入る場合だけ石を入れる */
    if (weight[i] <= c) {
        /* 石iがまだナップサックに入る場合 */
        put_value = memo[i + 1][c - weight[i]] + value[i];

    } else {
        /* もう石iがナップサックに入らない場合 */

        /* 価値は-1としておく(no_put_valueよりも必ず小さい値) */
        put_value = -1;
    }
    
    /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    /* 関数の実行結果をメモ */
    memo[i][c] = max_value;

    return max_value;
}

さらに、上記の knapsack_memo_kai の処理内容を knapsack_bottom_up 関数に組み込んだものが下記となります。

/************************************
 * 石の候補数N、ナップサックの容量Cの時のナップサック問題を解く
 * 戻り値：石の候補数N、ナップサックの容量Cの時の解
 ************************************/
int knapsack_bottom_up(void) {
    int i, c;
    int put_value;
    int no_put_value;
    int max_value;

    /* 小さな問題（iが大きい場合）から順に問題を解いていく */
    for (i = N; i >= 0; i--) {
        for (c = 0; c <= C; c++) {
            /* 石の候補i〜N-1、ナップサックの容量cの
               ナップサック問題を解く */
            if (i > N - 1) {
                /* もう入れる石がない */

                memo[i][c] = 0;
                continue;
            }

            /* 石iを入れなかった場合の最大価値を求める */
            no_put_value = memo[i + 1][c];

            /* 石iがナップサックに入る場合だけ石を入れる */
            if (weight[i] <= c) {
                /* 石iがまだナップサックに入る場合 */
                put_value = memo[i + 1][c - weight[i]] + value[i];

            } else {
                /* もう石iがナップサックに入らない場合 */

                /* 価値は-1としておく(no_put_valueよりも必ず小さい値) */
                put_value = -1;
            }
            
            /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
            if (no_put_value > put_value) {
                max_value = no_put_value;
            } else {
                max_value = put_value;
            }

            /* 関数の実行結果をメモ */
            memo[i][c] = max_value;
        }
    }

    /* 石の候補0〜N-1、ナップサック容量Cとした時の
       ナップサック問題の解を返却 */
    return memo[0][C];
}

ここで memo[i][c] の値が何であるかを思い出すと、これは knapsack_memo(i, c) の結果を格納するものであり、つまり memo[i][c] を求めるということは、knapsack_memo(i, c) を実行するのと同義の処理であると言えます。

ですので、この形式においても、より小さな問題（今回のナップサック問題の場合は i が大きな memo[i][c] の値）から解いていっているので、ボトムアップ方式の動的計画法であるといえます。

また、上記の knapsack_bottom_up 関数のループの内側の処理を見れば分かるように、これは要は下記の漸化式を解くのと同じ意味の処理となっています。

つまり、この漸化式さえ導き出してしまえば、この式をプログラムとして実行できるように実装し、あとは初期値となる i = N の時の memo[i][[c]] から順に、i を小さくしながら（つまり問題を大きくしながら）必要になる値を算出していくようにするだけで、ボトムアップ方式の動的計画法による解の算出を行うことができます。

ですので、ここまでの解説では、全探索を行う再帰関数を作成した後にトップダウン方式の動的計画法（メモ化再帰）を実現し、さらにそこからボトムアップ方式に変形するように説明をしてきましたが、この漸化式さえ導くことができれば、いきなり動的計画法で問題を解くことが可能です。

例えば、プログラミングコンテストや宿題などの問題文でいきなり漸化式が与えられるような場合、それはわざわざトップダウン方式（メモ化再帰）の動的計画法で解く必要がなく、その漸化式をそのまま実装し、あとは小さな問題から順に解くようにループを組んでやれば良いだけになります。

参考書等での動的計画法の説明で、いきなり漸化式の話が出てきて戸惑った方もおられるのではないでしょうか？

そんな方であっても、この節での説明のように問題の小さい方から解いていけば自然と漸化式の形式になることを知っておけば、動的計画法の説明で漸化式の話が出てくる理由も納得できるのではないかと思います！

動的計画法

ここまでナップサック問題を解きながら動的計画法について解説してきました。

最後にここまでの解説を踏まえて、動的計画法とは結局なんなのか？動的計画法を実装する時のコツはあるのか？について解説しておきたいと思います。

スポンサーリンク

動的計画法とは

動的計画法はナップサック問題のような “多数存在する組み合わせの中から最適な解を見つけ出す問題” を解く際によく用いられるアルゴリズムであり、具体的には下記の２条件を満たすアルゴリズムであると定義されています（Wikipedia から引用）。

1. 帰納的な関係の利用：より小さな問題例の解や計算結果を帰納的な関係を利用してより大きな問題例を解くのに使用する。

2. 計算結果の記録：小さな問題例、計算結果から記録し、同じ計算を何度も行うことを避ける。帰納的な関係での参照を効率よく行うために、計算結果は整数、文字やその組みなどを見出しにして管理される。

引用元：Wikipedia

一見難しそうな文章にも見えますが、おそらくこのページを読んでいただけた方であれば、この内容はすんなり頭に入ってくるのではないかと思います。

まず「1. 帰納的な関係の利用」で記述されていることは、つまりは ナップサック問題を小さな問題に分割して解く で解説した内容の話になります。

要は、解きたい問題をそのまま大きな問題として捉えるのではなく、小さな問題に分割し、その小さな問題の解を利用して大きな問題（解きたい問題）を解くような構造にしておく必要があるということです。

この小さな問題の解を利用して解きたい問題を解く構造は再帰関数を作成すれば自動的に構成できますので、再帰関数を作成することが帰納的な関係を利用する近道になると思います。

また「2. 計算結果の記録」で記述されていることは、つまりは トップダウン方式の動的計画法でナップサック問題を解く と ボトムアップ方式の動的計画法でナップサック問題を解く で解説した内容の話になります。

要は、小さな問題を解いた際にはその解をメモしておいて何回も同じ問題を解くことを避けるようにする必要があるということです。

つまり、簡単に言ってしまえば、要は下記の２つを満たした問題の解き方が動的計画法であるといえます。

• 大きな問題を小さな問題に分割し、大きな問題は小さな問題の解を利用して解く構造にする
• 小さな問題の解はメモしておき、同じ小さな問題を何回も解くことを避ける

ですので、ナップサック問題だけでなく、この２つを満たすことができる問題であれば動的計画法で解くことができます。

また、この動的計画法には、トップダウン方式の動的計画法でナップサック問題を解く で紹介したトップダウン方式のもの（大きな問題から先に解くことを試みる）と、ボトムアップ方式の動的計画法でナップサック問題を解く で紹介したボトムアップ方式のもの（小さな問題から先に解く）とが存在します（もしかしたら他にもあるかもしれません…）。

どちらも結局は、小さな問題の実行結果をメモしておき、次に同じ問題を実行する際にそのメモした結果を使い回すことで同じ問題を解くことを避ける手法になります。

つまり、両者ともに上記２つを満たした問題の解き方なので、どちらも動的計画法での解法であると言えると思います。要はアルゴリズムの考え方は同じで実装の仕方が異なるだけです。

また、トップダウン方式とボトムアップ方式のそれぞれのメリットは下記かなぁと思います。

• トップダウン方式のメリット：
  • 再帰関数からの発展が簡単（メモを利用するようにすれば良いだけ）
  • 本当に解く必要のある問題だけが解かれる
    • このおかげでナップサック問題の場合は計算量が C の大きさにあまり依存しない
    • （ボトムアップ方式の場合は計算量がダイレクトに C の大きさに依存する）
• ボトムアップ方式のメリット：
  • 漸化式からの発展が簡単（漸化式を満たすようにプログラミングすれば良いだけ）
  • 再帰呼び出しによるスタックオーバーフローの心配が不要
  • 計算量が見積もりやすい（ナップサック問題の場合の処理量はほぼ N * C に比例）

動的計画法で問題を解く場合は、このあたりのメリットや実装のしやすさを考慮して、トップダウン方式とボトムアップ方式のどちらを採用するかを決めてやれば良いと思います。

ただ、動的計画法と単に呼んだ時はボトムアップ方式の動的計画法の方、特に漸化式形式のものを指すことも多いので注意してください。この辺りは人やサイト、参考書等によって異なる気がします。それくらい動的計画法の定義は曖昧…。

動的計画法で解くためのコツ

最後に動的計画法で問題を解くためのコツについて、私なりの考えを述べておきたいと思います。

まずは全探索を行う再帰関数を作成する

トップダウン方式の動的計画法で解くとしてもボトムアップ方式の動的計画法で解くとしても、最初にまず考えるのは問題を再帰呼び出しを利用して全探索で解くことだと思います。

要は全探索を行う再帰関数を作成するのが動的計画法で問題を解く最初の一歩だと思います。

動的計画法を適用するためには、まず大きな問題を小さな問題の解を利用して解く構造にする必要がありますが、うまく動作する再帰関数を作成してしまえば自然とこの構造が成立することが多いです。

また、再帰関数が作成できた際には、その再帰関数で簡単な問題（解を求めるのに調べる必要のある組合せ数が少ない問題）を解いて、きちんとその再帰関数で問題が解けることを確認しておきましょう！

この再帰関数が動的計画法で問題を解く関数の土台になるので、この再帰関数で問題が解けないのであれば、当然動的計画法でも問題を解くことはできません。

全探索の再帰関数を動的計画法の再帰関数に発展させる

次は、その作成した全探索の再帰関数を動的計画法の再帰関数に発展させることを考えます。

トップダウン方式の動的計画法でナップサック問題を解く でも解説したように、再帰関数を作成してしまえば、あとは再帰関数を下記のように変更することで、割と簡単に動的計画法を用いた解法に発展させることができます。

• 再帰関数の実行結果を配列にメモするようにする
• 配列にメモが残っている場合、以降の再帰呼び出しは行わずにそのメモの値を返却するようにする

上記のように変更した再帰関数を大きな問題から解くように実行すれば、トップダウン方式の動的計画法を実現することができます（メモ化再帰）。

あとは、必要に応じて再帰関数を小さな問題から解くように実行するようにすれば、ボトムアップ方式の動的計画法を実現することができます。

例えばスタックオーバーフローが心配で再帰呼び出しを行いたくないような場合はボトムアップ方式の方が良いですし、”漸化式形式の動的計画法のプログラムのソースコードを提出せよ！” のような宿題のように漸化式形式のものが求められる場合は、ボトムアップ方式の動的計画法は漸化式から導ける の knapsack_bottom_up 関数のような形式まで発展させる必要が出てきます。

いきなり漸化式を考えるのもアリ

また、ボトムアップ方式の動的計画法でナップサック問題を解く の最後の方で解説していますが、ボトムアップ方式の動的計画法は漸化式を解くことそのものでありますので、いきなり漸化式を考えるのも良いと思います（そもそも問題文で漸化式が与えられるような場合は、そのままボトムアップ方式の動的計画法で解いてしまえば良いです）。

ですが、全探索を行う再帰関数を作成すれば、その再帰関数の構造そのものが漸化式を算出するヒントにもなりますので、何れにせよ再帰関数を作ることが動的計画法で問題を解く近道になると思います。

例えば、ナップサック問題を全探索を行う再帰関数 knapsack を ナップサック問題を小さな問題に分割して解く で紹介していますが、この関数から ボトムアップ方式の動的計画法でナップサック問題を解く で紹介した漸化式はすぐに導き出せるのではないかと思います（関数呼び出し部分を memo に置き換えれば良いだけ）。

再帰関数の実行結果に影響を与える要因を極力減らす

ここまでも説明してきたように、再帰関数さえ上手く作ってしまえばそこから動的計画法を適用するのは割と簡単だと思います。

ただ、再帰関数を上手く作るのが難しいですね…。

この再帰関数が動的計画法を適用するのに向いていない作りになってしまっていると動的計画法を適用しても効果が出にくい or メモリが足りなくて実行できなくなるようなことになりかねません。

例えば、ナップサック問題を小さな問題に分割して解く で紹介した knapsack.c における knapsack 関数は、下記のように作成したとしてもナップサック問題を解くことはできます。

/************************************
 * 石iから石N-1を入れた時の最大価値を求める
 * i：最初に入れるor入れないを試行する石の番号
 * c：ナップサックの空き容量
 * v：ナップサックに入っている石の価値の合計
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack_v(int i, int c, int v) {
    int put_value;
    int no_put_value;
    int max_value;

    if (i > N - 1) {
        return v;
    }

    no_put_value = knapsack_v(i + 1, c, v);

    if (weight[i] <= c) {
        put_value = knapsack_v(i + 1, c - weight[i], v + value[i]);
    } else {
        put_value = -1;
    }

    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    return max_value;
}

この knapsack_v 関数は、knapsack 関数から今現在ナップサックに入っている石の価値を引数 v として渡すように変更したものになります。

さらに、knapsack_v 関数をトップダウン方式の動的計画法（メモ化再帰）で解くようにしたものが下記の knapsack_v_memo になります。

/************************************
 * 石iから石N-1を入れた時の最大価値を求める
 * i：最初に入れるor入れないを試行する石の番号
 * c：ナップサックの空き容量
 * v：ナップサックに入っている石の価値の合計
 * 戻り値：石iから石N-1を入れた時の最大価値
 ************************************/
int knapsack_memo_v(int i, int c, int v) {
    int put_value;
    int no_put_value;
    int max_value;

    if (memo[i][c][v] != -1) {
        return memo[i][c][v];
    }

    if (i > N - 1) {
        memo[i][c][v] = v;
        return v;
    }

    no_put_value = knapsack_memo_v(i + 1, c, v);

    /* 石iがナップサックに入る場合だけ石を入れる */
    if (weight[i] <= c) {
        put_value = knapsack_memo_v(i + 1, c - weight[i], v + value[i]);
    } else {
        put_value = -1;
    }

    /* 石iを入れた場合と入れなかった場合の大きい方の価値を返却 */
    if (no_put_value > put_value) {
        max_value = no_put_value;
    } else {
        max_value = put_value;
    }

    memo[i][c][v] = max_value;

    return max_value;
}

トップダウン方式の動的計画法でナップサック問題を解く で紹介した knapsack_memo 関数に対する knapsack_v_memo 関数の違いは、knapsack_v 関数と knapsack 関数との違い同様に、今現在ナップサックに入っている石の価値を引数 v として渡す点です。

knapsack_memo 関数では、関数の結果（返却値）が引数 i と引数 c のみによって決まります。

ですので、メモを取るための配列 memo は、下記のように引数 i と引数 c それぞれが取りうる値全てを区別してメモが取れる分のサイズがあれば良いです（i のとりうる値を 0 〜 N、c のとりうる値を 0 〜 C とし、さらに配列の型は int である前提としています）。

int memo[N + 1][C + 1];

その一方で、knapsack_v 関数の場合、関数の結果は引数 i と引数 c だけでなく引数 v の影響も受けて決まることになります。

したがって、メモを取るための配列 memo は、下記のように引数 i と引数 c と引数 v それぞれが取りうる値全てを区別してメモを取れるようにサイズを設定する必要があります（v のとりうる値を 0 〜 V としています）。

int memo[N + 1][C + 1][V + 1];

つまり、knapsack_memo 関数の時に比べて、knapsack_v_memo 関数の場合、メモを取るための配列を用意するために、V + 1 倍 のメモリが必要になります。

例えば N + 1 = 512、C + 1 = 2048、V + 1 = 16384 である場合、knapsack_memo 関数で使用する配列 memo に必要なメモリのサイズは 512 * 2048 * 4 ≒ 4MB （4 は int 型のサイズ）ですが、knapsack_memo 関数で使用する配列 memo に必要なメモリのサイズは、その 16384 倍の 64GB のメモリが必要になってしまいます。

64GB のメモリが必要であるとなると、多くの PC では実行不可になってしまうと思います。

つまり、knapsack_memo では簡単に解けてしまうような問題も、knapsack_v_memo ではメモリが足りなくてプログラムの実行すらできなくなってしまいます。

そして、この knapsack_memo は全探索を行う再帰関数 knapsack から、knapsack_v_memo は全探索を行う再帰関数 knapsack_v から発展させることで作成した関数ですので、結局は全探索を行う再帰関数の作り方がまずいと、動的計画法を適用した場合にメモリを大量に消費してしまうようなことになってしまうと言えます。

上記のことは、トップダウン方式だけではなく、ボトムアップ方式の動的計画法においても同様のことが言えます。

ですので、動的計画法を適用することを考えれば、全探索を行う再帰関数はできるだけ関数の実行結果に影響を与える要因（再帰関数実行中に値が変化する変数）を減らして作成するようにする必要があります。

もし動的計画法で解こうとして、メモを取る配列の次元数が大きくなってしまうような場合は、関数の実行結果に影響を与える要因を減らすことができないかどうかを考えるようにしましょう！

動的計画法に慣れる

こういった再帰関数の作成や動的計画法に慣れるためには、やはり実践を積むのが一番手っ取り早いと思います。

例えば paiza なんかだと下記ページに動的計画法で解ける練習問題が紹介されていますので、まずは動的計画法を使ってみたいという方は挑戦してみると良いかと思います。

https://paiza.jp/works/mondai/dp_primer

また「動的計画法 atcoder」なんかでググれば、AtCoder（プログラミングコンテスト）で出題された “動的計画法で解くことのできる問題” が紹介されているページも多数見つかるので、そこで紹介されている問題を解いてみるのも良いと思います。

まとめ

このページでは、まずナップサック問題を解きながら動的計画法について解説し、最後に動的計画法がどのようなアルゴリズムであるかについて解説しました！

動的計画法とは簡単にいうと下記を行うアルゴリズムになります。

• 大きな問題を小さな問題に分割し、大きな問題は小さな問題の解を利用して解く構造にする
• 小さな問題の解はメモしておき、同じ小さな問題を何回も解くことを避ける

ナップサック問題を解く を読んでいただいた方であれば実感していただけたのではないかと思うのですが、動的計画法は考え方としては非常に単純なアルゴリズムです。

大きな問題を小さな問題の解を利用して解く再帰関数を作成してしまえば、下記のように論理展開・関数の変更をしていけば、簡単に動的計画法による解法に導くことができます。

• 再帰関数の処理が遅い…
  → もしかしたら再帰関数が同じパラメータで何回も実行されているのかも！
  　→ メモをとって同じパラメータで実行される場合はそのメモを使い回せば速くなるはず！

これだけでトップダウン方式の動的計画法（メモ化再帰）を実現することができます。

あとは、このメモを行う再帰関数を小さな問題側から解くように実行するようにすれば、ボトムアップ方式の動的計画法も実現できます。

ただし、動的計画法の考え方は簡単ですが、動的計画法を使いこなすのは難しいと思います。上手く再帰関数を作成する必要がありますし、そもそも解きたい問題に動的計画法をうまく適用できるかどうかの見極めも難しいです。

これらの勘所を身につけるためには、やっぱり実践で慣れるのが一番手っ取り早いと思いますので、動的計画法に慣れる で紹介したようなサイトを利用して、たくさん問題を解いてみることをオススメします！

私も最近やっと paiza や AtCoder をやるようになったので、問題を解いていて気づいた点など出てきた際には、また記事にして紹介していきたいと思います！