番兵法についてわかりやすく解説

このページでは、番兵法について解説します！

ソースコード等は C言語 で記述していますが、ソースコードは単純ですし、考え方についても他のプログラミング言語を使用されている方にも理解していただける内容だと思いますので、是非いろんな方に読んでいただければと思います！

番兵法とは

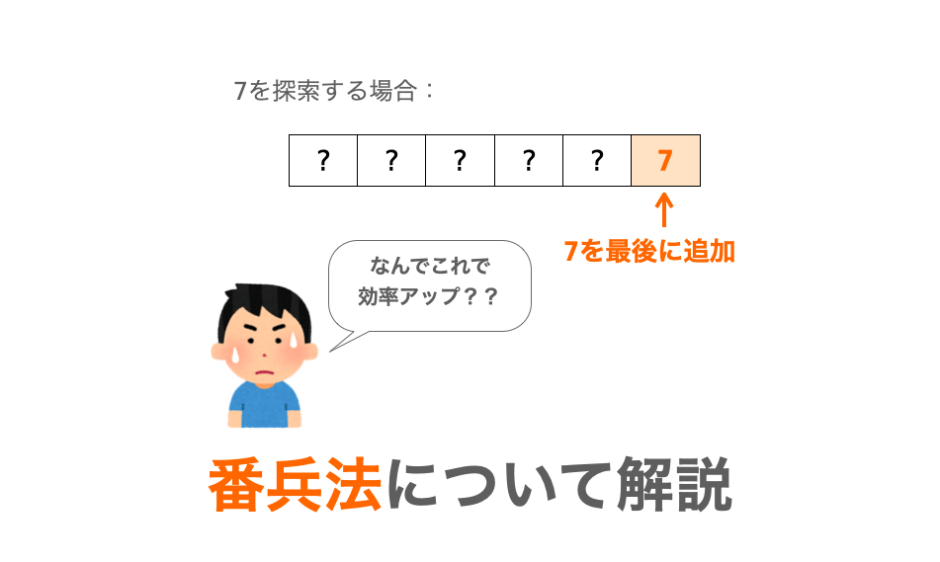
番兵法とは、データ列の最後に “終端を表すダミーのデータ” を追加し、それを上手く利用して処理効率を向上させる手法（テクニック）になります。

この “終端を表すダミーのデータ” のことを “番兵（ばんぺい）” と呼びます（英語だと sentinel）。

番兵の分かりやすい例は、C言語 における文字列の終端を表すヌル文字 '\0' です。この文字があるので、C言語 では文字列の文字数が分からなくても文字列を上手く扱うことが可能です。

ただ、このヌル文字は文字列の終端を表すだけのデータであり、処理の効率を向上させる目的のデータではありません。

番兵法では、処理の効率を向上させる目的で番兵を用意し、この番兵をうまく利用することで処理の効率を向上させるテクニックとなります。

線形探索を番兵法で効率化

この番兵法が最もよく使用されるケースが、データ探索アルゴリズムの１つである “線形探索” の探索効率を向上させたい時です。

ということで、線形探索を実例として番兵法の仕組みや、番兵法で探索効率が向上する理由について解説していきたいと思います！

もし線形探索をご存知ない方は、下記ページで詳しく解説していますのでこちらを参照していただければと思います。

【C言語】データの探索アルゴリズム（線形探索・二分探索）について解説

ただ、線形探索の処理内容自体は単純ですし、番兵法を理解するだけであれば、このページの内容だけでも十分ではないかと思います。

スポンサーリンク

単純な線形探索

C言語 で単純な線形探索を記述すれば、下記のような処理となります。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* 線形探索 */
    for (i = 0; i < num; i++) {
        if (array[i] == x) {
           break;
        }
    }

    return i;
}

上記の search 関数では、配列 array の中から整数 x を探索する処理を行なっています。

num は配列に格納されている整数の個数を表す変数であり、array[0] 〜 array[num - 1] に探索対象となるデータが事前に格納されているものとしています。

また search 関数は、配列の中から整数 x が見つかった場合は x が見つかった位置（配列の添字 i）を返却し、見つからなかった場合は num を返却します。

以降でも、search 関数は何度も登場しますが、特筆しない限り、各変数や返却値は全て上記の意味のものとして解説していきます。

では、関数内部でどのような処理が行われているのかの詳細を確認していきましょう。

まず i に対する for ループの中では、配列の添字 i の位置の要素、すなわち array[i] と整数 x の比較を行なっています。

for 文により、i を 0 から順に 1 ずつ増加させていっていますので、要は先頭の要素 array[0] から順番に、配列の添字を 1 ずつ増やしながら１つずつ整数 x と一致するかどうかの比較を行なっていることになります。

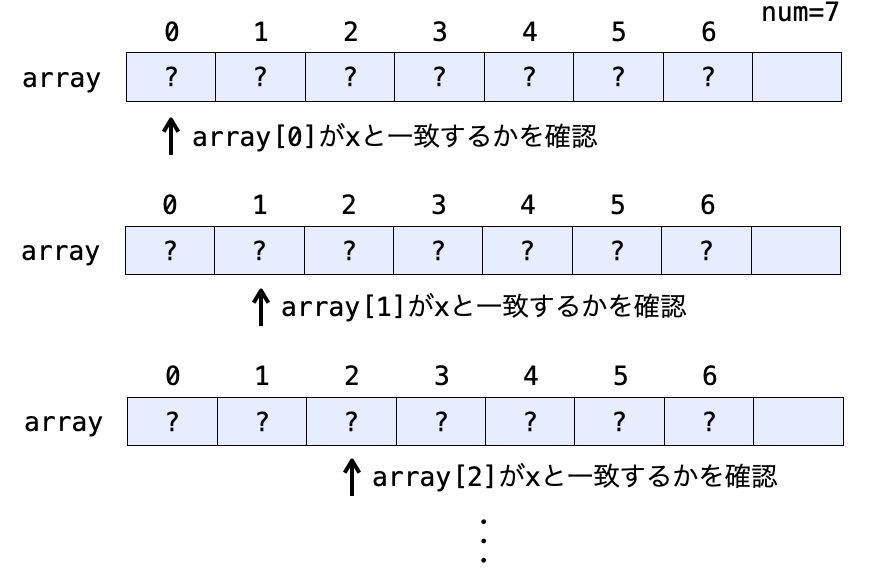
array[i] と x が一致した場合、つまり if (array[i] == x) が成立した場合、その添字 i の位置にデータが見つかったことになりますので、break によりループを抜け出し、その時点の i の値を return して返却しています。

if (array[i] == x) が成立して break でループを抜け出した場合、この return で返却される i の値は num よりも必ず小さい値になります。

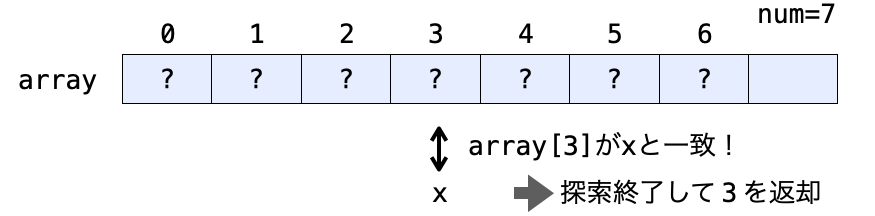
もし、if (array[i] == x) が一回も成立しないまま i が num になるまで増加した場合、for 文の中に記載された継続条件 i < num が不成立となって、for ループが終了して探索が終了することになります。

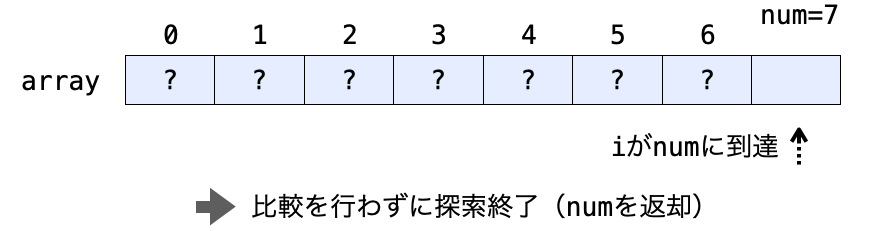
この場合、array[0] 〜 array[num - 1] の中に x は存在しなかったことになりますので、見つからなかった場合の返却値である num を返却します（for ループを抜けた後に i を返却していますが、探索したいデータ x が存在しなかった場合、for ループを抜けた時点で i は必ず num になっているため、i を返却すれば num を返却することになります）。

線形探索を for ループで行う処理の流れは上記のようになります。

次は、上記の for ループを、実行されている比較と終了条件がより分かりやすくなるように while ループで書き換えてみたいと思います。この場合、search 関数は下記のように記述することができます。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* 線形探索 */
    i = 0;
    while (1) {
        
        if (i >= num) {
            break;
        }

        if (array[i] == x) {
            break;
        }

        i++;
    }

    return i;
}

動作としては先程の for ループとほぼ同じなのですが、１回のループの中で比較が２回行われていることがより分かりやすくなったのではないかと思います（特に for ループの場合、i  と numとの比較がループの中で毎回行われている点がちょっと分かりにくい）。

つまり線形探索を行う際には、ループの中で毎回下記の２つの比較が行われています（比較が成立した際には break で探索を終了する）。

• i >= num の比較（前述の for ループの場合は i < num の比較）
• array[i] == x の比較

後者の array[i] == x の比較に関しては、データを探索するための比較なので必ず必要です。でも前者 i >= num の比較は必要でしょうか？

ここまで解説してきた線形探索においては必要ですね！

探索したいデータが配列内に存在しない場合、i >= num の比較がないと、無限にループが続いてしまいます（いずれは配列外の要素にアクセスしようとして、プログラムが落ちたり例外が発生したりします）。

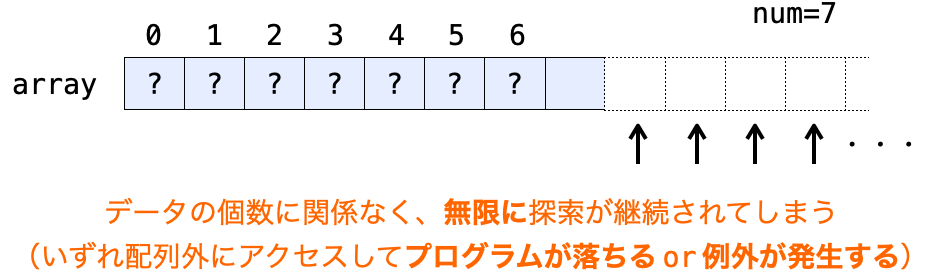
ただ、i >= num の比較が必要なのは、あくまでも “探索したいデータが配列内に存在しない場合” のみです。

もし配列内に必ず探索したいデータが存在するのであれば、いずれは必ず array[i] == x の比較が成立してループが終了しますので、この場合は i >= num の比較は不要ですね！

番兵法を用いた線形探索

番兵法とはまさに、先ほど説明した “配列内に必ず探索したいデータが存在するのであれば i >= num の比較は不要である” の考えに基づいた手法になります。

でも、”配列内に必ず探索したいデータ” が存在するとは限らないですよね…（そもそもそれが分かっているのであれば探索しなくてもいい場合もあるはず…）。

なので番兵法では、必ず探索したいデータが配列内に存在するようにするため、配列内に探索したいデータをダミーのデータとして格納します（このダミーのデータが “番兵”）。

より具体的には、配列内のデータ列の末尾の次の位置に、探索したいデータをダミーのデータとして格納します。

例えば、配列 array の array[0] 〜 array[num - 1] の位置にデータが格納されている場合、array[num] に対して探索したいデータ x を格納します（すなわち array[num] = x; を実行する）。

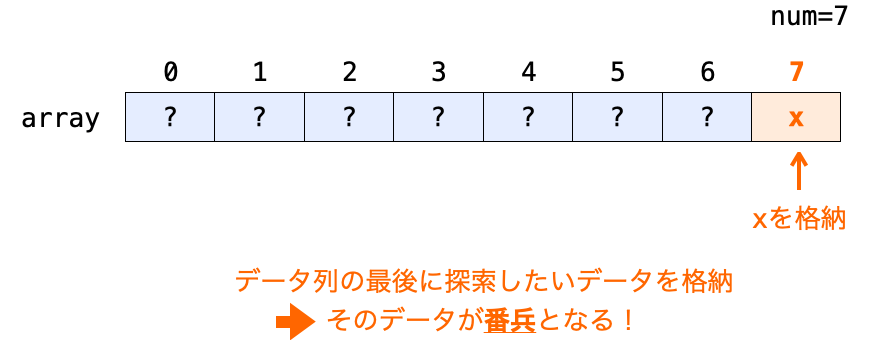
そうすれば、たとえ線形探索時に i が 0 〜 num - 1 の場合に array[i] == x が成立しなかったとしても（つまり、配列内の num 個のデータの中に x が存在しなかったとしても）、i が num になった際に必ず array[i] == x が成立し、確実にこの時点でループを終了することができます。

要は、追加で格納したダミーのデータが見張り番となり、それ以降は進んではいけない（探索しなくていい）ことを教えてくれるわけです。そういった意味合いから、このダミーのデータは番兵と呼ばれます。

ただし、i が num 未満の時に array[i] == x が成立するのと、i が num の時に array[i] == x が成立するのとでは、意味合いが大きく異なる点に注意してください。

前者の場合は、元々配列内に存在していた array[0] 〜 array[n - 1] のいずれかが x と一致したことになるので、x が配列内に存在していたことになります。

その一方で後者の場合、元々配列に存在していなかったダミーのデータと x が一致しているだけであり、array[0] 〜 array[n - 1] の全てが x と一致しなかったことになるので、x は元々の配列内には存在しなかったことになります（もし存在していたらその時点で探索は終了している）。

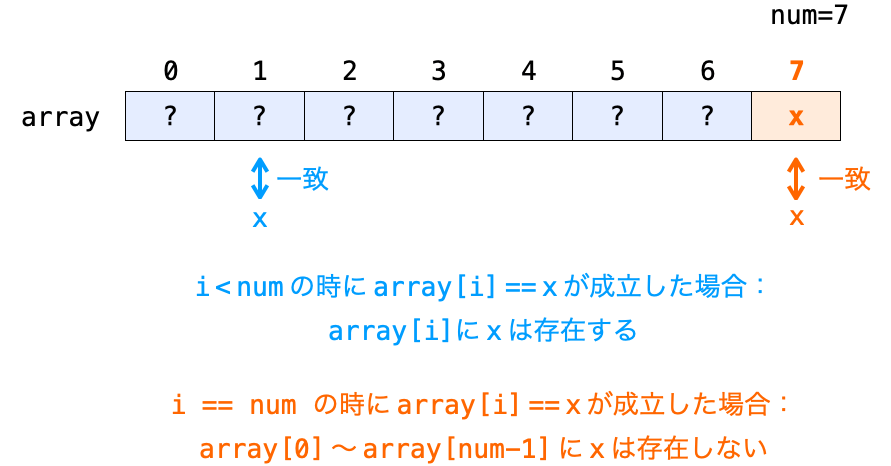
で、本題に戻ると、array[num] = x によりデータの終端を表すダミーのデータ（探索したいデータ）を設けることで、探索したいデータが配列内に存在しなくてもデータの終端を探索する際に必ず array[i] == x が成立するようになります。

ですので、わざわざ i と num の比較を行わなくても、ループ処理は自動的に終了します。したがって、この場合、i と num の比較は不要になります。

つまり、線形探索に番兵法を適用した場合、ループ内で行う比較は下記の１つのみで済むことになります。

• array[i] == x の比較

単純な線形探索に比べれば、比較回数は約半分になりますので、その分探索効率を向上させることが望めます。

こんな感じで、データ列の最後の次の位置にダミーのデータ（番兵）を追加し、それにより比較回数を削減することで、探索効率を向上させるのが、番兵法になります。

単純な線形探索で紹介した while ループでの線形探索の処理に対して番兵法を適用すれば、下記のように記述することができます。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* ダミーのデータを格納 */
    array[num] = x;

    /* 線形探索 */
    i = 0;
    while (1) {

        if (array[i] == x) {
            break;
        }

        i++;
    }

    return i;
}

単純な線形探索に比較して、while ループの中の下記の処理がそのまま削減されていることが確認していただけると思います。

if (i >= num) {
    break;
}

上記の比較処理が削減されている分、単なる線形探索法に比べて、番兵法の方が探索効率が向上します。

番兵法を適用した線形探索のいろいろな記述の仕方

番兵法を適用した線形探索はさまざまな記述の仕方が可能です。

例えば、上記の番兵法を用いた線形探索の書き方を変形すれば、下記のようにスマート？な書き方もできます。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* ダミーのデータを格納 */
    array[num] = x;

    /* 線形探索 */
    i = 0;
    while (array[i] != x) i++;

    return i;

さらに、for ループでの線形探索に対して番兵法を適用した場合は下記のように記述することができます（for 文の中の継続条件が不要になる）。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* ダミーのデータを格納 */
    array[num] = x;

    /* 線形探索 */
    for (i = 0;; i++) {
        if (array[i] == x) {
            break;
        }
    }

    return i;
}

もうちょっと変形すれば、下記のようにも記述することができます。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* ダミーのデータを格納 */
    array[num] = x;

    /* 線形探索 */
    for (i = 0; array[i] != x; i++);
    
    return i;
}

いずれにしても、i と num との比較が削減されていることが確認できると思います。

スポンサーリンク

番兵法の実装時の注意点

次は、番兵法を実装する際に注意すべき点をいくつか挙げておきます。

配列のサイズ

番兵法を適用する際に注意が必要なのは “配列のサイズ” です。

元々配列に格納するデータよりも余分にデータを１つ格納する必要があるため、その分配列のサイズを多めに設定しておく必要があります。

番兵を格納する位置

また、ここまではデータ列の先頭側から順に探索を行う例で解説してきましたが、データ列の末尾側から順に探索を行うことも可能です。

この場合は、”配列の先頭” にダミーのデータを用意する必要があります。要は、ダミーのデータを格納するのは、一番最後に比較が行われる位置です。

下記は末尾から順にデータを探索する番兵法を適用した線形探索の例になります。array[1] 〜 array[num] に探索対象となるデータが事前に格納されている前提で記述しています。

また、array[1] 〜 array[num] の中に探索したいデータ x が存在しなかった時には 0 を返却するようにしています。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* ダミーのデータを格納 */
    array[0] = x;

    /* 線形探索 */
    i = num;
    while (1) {
        if (array[i] == x) {
            break;
        }
        i--;
    }

    return i;
}

もし、末尾側から探索を行うのにダミーのデータを末尾側に格納してしまうと、最初にダミーのデータと探索したいデータが一致してしまい、本当に探索をしたいデータの探索を行う前にループが終了してしまうので注意してください。

番兵法を用いた場合の処理時間

次に、単純な線形探索と、番兵法を適用した際の線形探索とで処理時間の比較を行なってみたいと思います。

単純な線形探索は、下記の search 関数によって行います（単純な線形探索の後半で紹介した search 関数）。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* 線形探索 */
    i = 0;
    while (1) {
        
        if (i >= num) {
            break;
        }

        if (array[i] == x) {
            break;
        }

        i++;
    }

    return i;
}

さらに、番兵法を適用した線形探索は、下記の search 関数によって行います（番兵法を用いた線形探索で紹介した search 関数）。

unsigned int search(int array[], int x, unsigned int num) {
    unsigned int i;

    /* ダミーのデータを格納 */
    array[num] = x;

    /* 線形探索 */
    i = 0;
    while (1) {

        if (array[i] == x) {
            break;
        }

        i++;
    }

    return i;
}

これらの search 関数の呼び出し前後の時刻を計測し、その差を処理時間として比較を行いました（最適化はオフしてコンパイル）。

データの個数 num は 100000000 としています。さらに、search の中に存在しないデータを探索した時の処理時間の比較を行います（一番時間がかかる時の処理時間）。

結果は下記の通りとなりました。

• 単純な線形探索：約 0.31 秒
• 番兵法を用いた線形探索：約 0.27 秒

実行する度にばらつきはあるものの、大体上記のような処理時間になりました。

確かに、若干速くなってはいるものの、思ったよりも探索効率は向上していないなぁという印象です。おそらく同じ印象を持たれた方も多いと思います。

比較回数に関してだけ言えば確かに約半分に減っていると思いますが、線形探索中に実行される処理は他にもありますので（足し算やループを回す処理など）、全体としては約１０％程度の処理しか削減できていないということなのかなぁと推測します。

ただ若干は速くなると思いますので、どうしても線形探索の処理時間を少しでも減らしたいという場合は有効な手段だと思います。

番兵法のメリット・デメリット

最後に番兵法のメリットとデメリットについて解説しておきます。

スポンサーリンク

メリット

まずはメリットです。

お手軽に比較回数が減らせる

これはここまでの解説でも述べてきましたが、比較回数を減らすことができる点はメリットです。

ただし、処理時間的には 番兵法を用いた場合の処理時間 で紹介したようにそこまで劇的に減らすことはできない点には注意が必要だと思います。

劇的に処理時間を向上させたいのであれば、下記ページで紹介している二分探索などアルゴリズムを用いる方が有効だと思います。

【C言語】データの探索アルゴリズム（線形探索・二分探索）について解説

ただ、これは上記ページにも書いていますが、二分探索の場合、データ列がソートされている必要があります。

一般に、探索よりもソートの方が処理時間はかかりますので、探索直前にソートをするようではむしろ遅くなってしまいます。

なので、線形探索から二分探索に置き換えるような場合は、探索を行う部分だけでなく、データを格納する部分の変更も必要になり、大掛かりな変更となってしまいます。

それに対し、番兵法では変更が必要なのは探索を行う部分だけですし、変更も簡単です。このお手軽に高速化を図れるという点が、この番兵法の良いところだと思います。

デメリット

続いてデメリットです。

可読性が下がる

まず、ちょっとソースコードが読みにくくなりますね…。

番兵法を適用したループ処理は、パッと見だと終了条件が足りないように見えてしまいます（データが見つからない場合に配列外まで探索が行われるように見える）。

また、いきなり配列に探索したいデータを格納する処理も、おそらく番兵法を知らない方がみると謎な処理に見えてしまうと思います。

もちろん処理をじっくり紐解けば、それでループもしっかり終了し、探索したいデータを格納する処理も理解できるとは思いますが、特に番兵法を理解していない方にはソースコードが読みにくいと思われる可能性が高いです。

効果があまり出ない場合も多い

番兵法を用いた場合の処理時間 でも紹介しましたが、番兵法を用いることで確実に比較回数を減らすことは可能ですが、処理時間としてはそこまで劇的な変化はありません。

もしかしたら環境を変えれば処理時間の差がはっきり出る可能性もありますが…。

また、そもそも番兵法の効果が出にくいようなケースも多々あります。

例えば文字列を線形探索するような場合、下記のように strcmp を用いてデータの一致を確認すると思います。

i = 0;
while (1) {
    if (i >= num) {
        break;
    }

    if (strcmp(array[i], x) == 0) {
        break;
    }

    i++;
}

この場合、strcmp の処理の方が、i >= numのような単なる整数同士の比較よりも処理時間が長いので、i >= num の比較を削減できたからといって、探索効率はそんなに変わらないと思います。

要は、番兵法により削減できる比較よりも処理時間が長い処理がループの中に存在すると、その比較を削減したからといってそんなに旨みは無いです。

例えばですが、上記の処理において strcmp の中で比較処理が 10 回行われているとすると（strcmp の中では文字同士の比較が行われる）、番兵法で i >= num の比較を削減したとしても、全体の比較回数としては 1/11 しか削減できないことになります（さらに比較以外の処理も行われるので、削減できる処理の割合はもっと少なくなる）。

メモリ使用量が増える

また、ダミーのデータを配列に格納する必要があるため、その分のメモリ使用量が増えます。

一応デメリットとして挙げていますが、増えるメモリ使用量はデータ１つ分のみですので、無視して良い程度のデメリットだと思います（ただし、２次元配列などに対して番兵法を用いる場合は、もっと必要になるデータ量が増えるので注意）。

まとめ

このページでは、番兵法について解説を行いました！

番兵法は、データ列の最後にダミーのデータ（番兵）を追加し、それを利用することで処理効率を向上させるテクニックになります。個人的には、この番兵法は綺麗なテクニックですごく好きですねー。

特に番兵法が用いられるのが線形探索時で、ループの終了条件（もしくは継続条件）を判断する際の比較を１つ減らすことができ、これにより探索効率を向上することができます。

お手軽に高速化が図れるというメリットがある反面、ソースコードの可読性が下がる可能性もありますので、本当に必要な場合のみ番兵法を用いるのが良いのかなぁと思います。

ただし、劇的に探索速度が向上するというわけでは無いので注意してください（計算量のオーダーは変わらない）。

特にデータ量の多いような時に、劇的に探索速度を向上させる探索アルゴリズムとして二分探索があります。

二分探索に関しては下記ページで紹介していますので、興味のある方はぜひ読んでみてください！

【C言語】データの探索アルゴリズム（線形探索・二分探索）について解説