KMP法についてわかりやすく解説（C言語サンプル付き）

このページにはプロモーションが含まれています

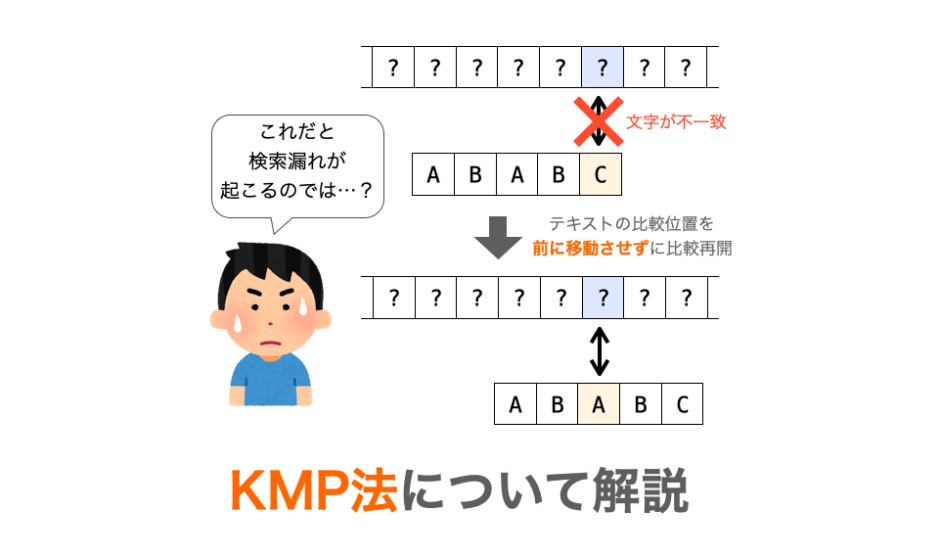
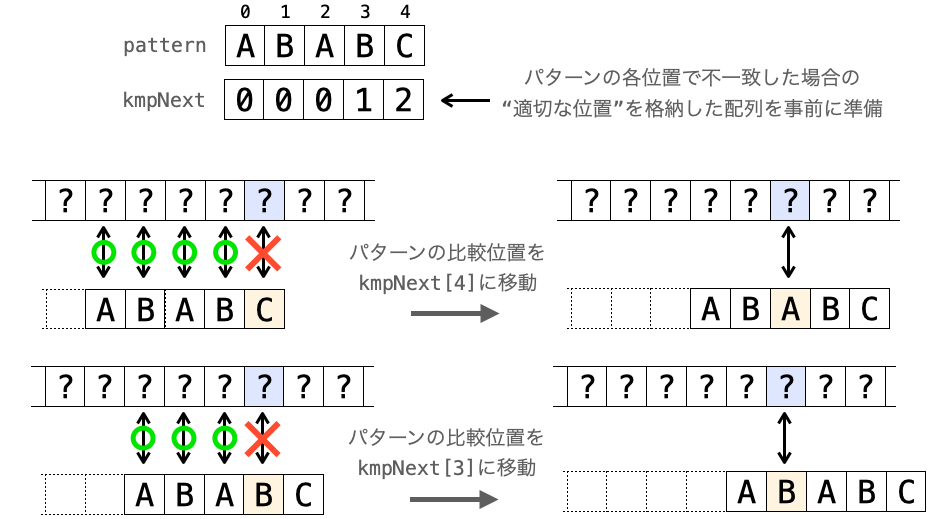
今回は文字列検索アルゴリズムの１つである「クヌース – モリス – プラット法」、略して KMP 法について解説していきたいと思います。

正直言って、この KMP 法はかなりややこしいアルゴリズムだと思います。参考書などで KMP 法のプログラムのソースコードを見た時に、なぜこれでうまく文字列検索が行えるのかと疑問を抱いた方も多いのではないでしょうか（私だけ？）。

このページではこのような疑問を抱えている方に向けて、”なぜ KMP 法で漏れなく検索できるのか？” や “どのように実装すれば効率的に処理が行えるのか？” のあたりが直感的に分かるように KMP 法を解説をしています（解説をしているつもりです…）。

なので、解説はかなり長いです…。

もしすぐに KMP 法の文字列検索プログラムのソースコードを読みたい方は最終的な KMP 法の文字列検索プログラムまでスキップしていただければと思います。

MEMO

このページでは、テキスト（text）を検索先の文字列、パターン（pattern）を見つけ出す文字列として解説を行なっていきます

つまり、このページにおける文字列検索とは、”テキスト” の中から “パターン” を見つけ出す処理となります

Contents

力まかせ法の復習
KMP 法
- KMP 法とは
- KMP 法と力まかせ法の違い
KMP 法の仕組み
KMP 法の実装方法
- “適切な位置” を求める
- 文字の不一致時に “適切な位置” から比較を再開する
最終的な KMP 法の文字列検索プログラム
KMP 法の計算量
まとめ

力まかせ法の復習

KMP 法をしっかり理解するためには、まずは “力まかせ法” について理解しておいた方が良いです。これは、KMP 法が “力まかせ法を改良した文字列検索アルゴリズム” だからです。

なので、まずは簡単に力まかせ法について復習したいと思います。力まかせ法の詳細は下記ページで解説していますので、詳しく知りたい方は下記ページを参考にしていただければと思います。

力まかせ法（単純な文字列検索方法）について解説（C言語サンプル付き）

力まかせ法は、パターンが存在する可能性のあるテキストの位置を “総当たり” で調べる文字列検索アルゴリズムです。

この力まかせ法は、パターン自体をずらしながらパターンが存在するかどうかを調べることで実現することが出来ます。

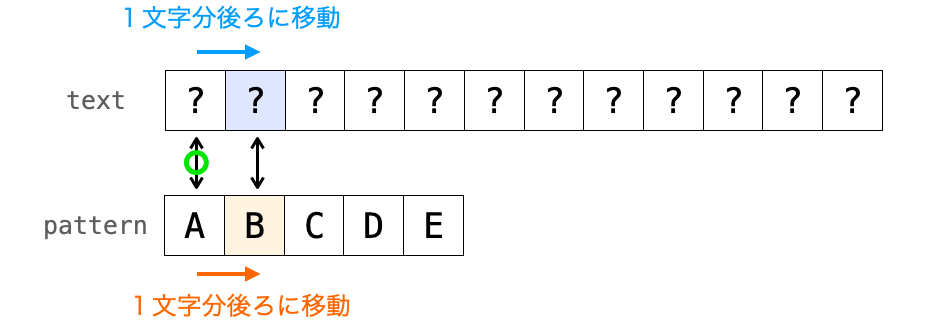
力まかせ法では、まずテキストの先頭にパターンが存在しないかどうかを判断するために、パターンの先頭とテキストの先頭の文字とを比較します。

もし文字が一致すれば、テキストとパターンの比較位置それぞれを１つ後ろにずらして比較を再開します。

文字が一致している場合はこの繰り返しで、パターンの文字全てで比較が一致すれば、パターンの先頭の文字と比較を行なったテキストの位置にパターンが見つかったことになります。

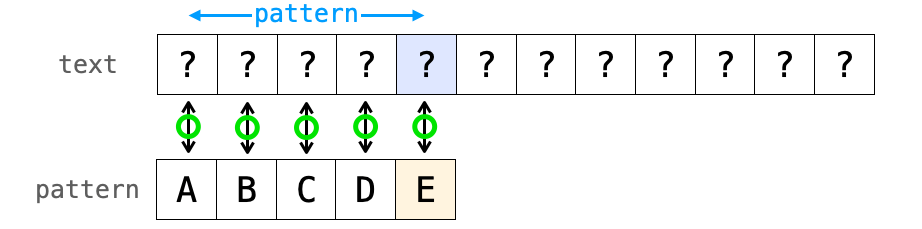
その一方で、文字が不一致した場合はテキストの先頭にそのパターンは存在しないことが判明します。

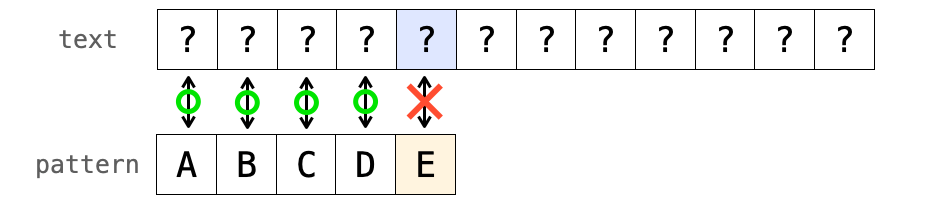
この時に、力まかせ法では、テキストの次の文字の位置にパターンが存在するかどうかを判断するために、パターン自体を１文字分後ろにずらし、パターンの “先頭” から比較を再開します。

後は上記の繰り返しで、文字が一致している間はテキストとパターンの比較位置を１文字ずつずらしながら比較を繰り返します。パターンの文字全てで比較が一致すれば、パターンの先頭と比較を行なったテキストの位置にパターンが見つかったことになります。

文字が不一致した場合も同様で、パターン自体を１文字後ろにずらし、パターンの先頭から比較を再開します。

パターンが存在する可能性のあるテキストの位置全てに対して上記の処理を繰り返し行うことで、テキストからパターンを見つけ出すのが力まかせ法です。総当たりで比較を行うので、パターンの検索漏れは起こりません。

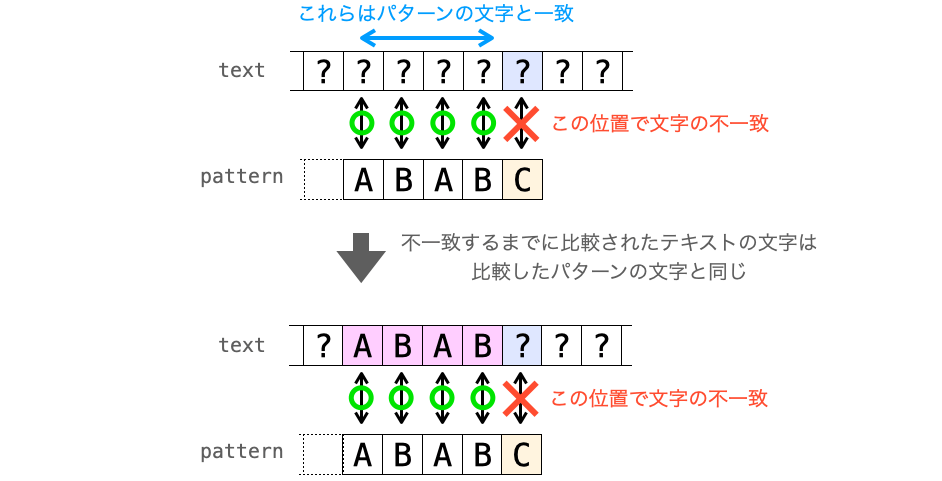
ここで、（パターン自体をずらした文字数ではなく）テキストの比較位置とパターンの比較位置に注目すると、これらは下記のように変化していくことになります。

文字の比較が一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：１文字分後ろ側に移動
先頭の位置で比較が不一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：先頭に移動
先頭の位置 “以外” で比較が不一致した場合：
- テキストの比較位置：直前の比較で一致した文字数 - 1 文字分前側に移動
- パターンの比較位置：先頭に移動

先頭の文字 “以外” で比較が不一致した場合のテキストの比較位置がちょっと分かりにくいかもしれないですが、下の図を見るとなぜ 直前の比較で一致した文字数 - 1 文字分前側に移動するのかが理解できると思います。

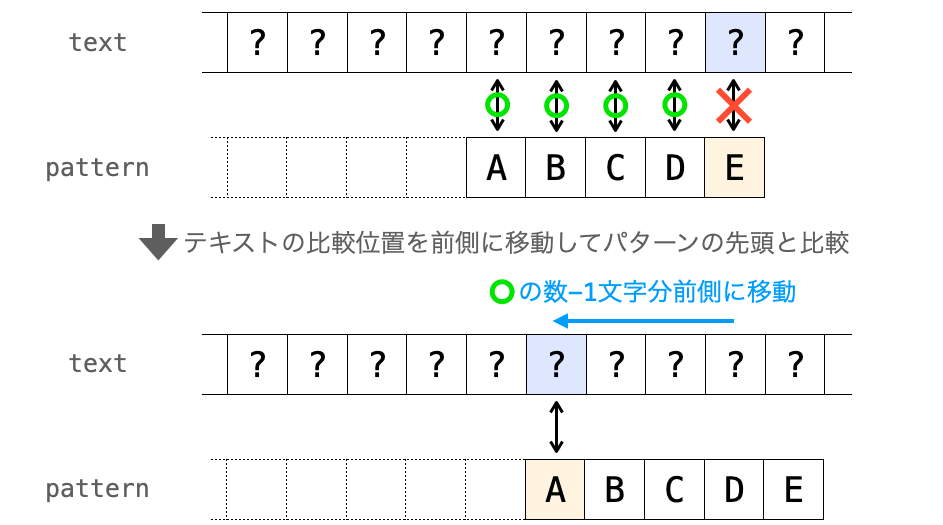
上記のようにテキストの比較位置とパターンの比較位置を移動させながら比較を行なっていくことで、力まかせ法による文字列検索を実現することができます。

この例が下記の forceSearch 関数になります。

力まかせ法

int forceSearch(char text[], int text_len, char pattern[], int pattern_len) {
    int text_pos; /* テキストの比較位置 */
    int pattern_pos; /* パターンの比較位置*/

    /* パターンの比較位置を先頭にセット */
    pattern_pos = 0;

    /* テキストの比較位置を先頭にセット */
    text_pos = 0;

    /* テキストの比較位置がテキストの最後を超えるまでループ */
    while (text_pos < text_len) {
        /* テキストの比較位置の文字とパターンの比較位置の文字が一致するかを判断 */
        if (text[text_pos] == pattern[pattern_pos]) {
            /* 一致した場合 */

            /* パターンの最後の文字までテキストの文字が一致したかどうかを判断 */
            if (pattern_pos == pattern_len - 1) {
                /* パターンが存在するテキストの位置を返却 */
                return text_pos - pattern_pos;
            }

            /* テキストとパターンの比較位置を１文字分後ろ側に移動する */
            text_pos++;
            pattern_pos++;

        } else {
            /* 不一致した場合 */

            /* 不一致した位置が先頭の位置であるかを判断 */
            if (pattern_pos == 0) {
                /* 先頭の位置で比較が不一致した場合 */

                /* テキストの比較位置を１文字分後ろ側に移動する */
                text_pos++;

                /* パターンの比較位置を先頭に移動する */
                pattern_pos = 0;
            } else {
                /* 先頭の位置以外で比較が不一致した場合 */

                /* テキストの比較位置を前側に移動する */
                text_pos -= (pattern_pos - 1);

                /* パターンの比較位置を先頭に移動する */
                pattern_pos = 0;
            }
        }
    }

    /* パターンが見つからなかった場合は-1を返却 */
    return -1;
}

これは、ちょうど下記ページの力まかせ法の別の実装で紹介している関数になります。

力まかせ法（単純な文字列検索方法）について解説（C言語サンプル付き）

この力まかせ法で残念なのが、”テキストの比較位置が前側に移動してしまう” ことがあるところです。前側に移動することで、テキストの同じ位置で何回も比較が行われることになり、これが力まかせ法の検索効率低下の原因になります。

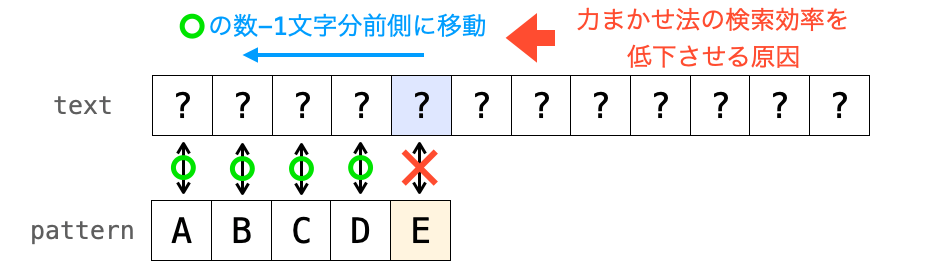
この問題を解決するのが、このページで解説する KMP 法になります。

このページで説明する KMP 法は、”テキストの比較位置の前側への移動” を行うことなく文字列が検索できるように力まかせ法を改良した文字列検索アルゴリズムになります。

KMP 法

では続いて、このページの本題である KMP 法について解説していきたいと思います。

KMP 法とは

最初にざっくり説明しておくと、KMP 法とは「文字の比較が不一致した際に、その “不一致した位置” と “パターンの文字列” から求まる “適切な位置” から比較を再開することで効率的に検索を行う文字列検索アルゴリズム」です。

ちょっとイメージが湧かないかもしれませんが、次の力まかせ法との違いを理解すると、KMP 法についてグッとイメージがつきやすくなると思います。

KMP 法と力まかせ法の違い

力まかせ法の復習で解説したように、力まかせ法で文字列を検索する際には、テキストの比較位置とパターンの比較位置を下記のように移動させながら比較が行われます。

文字の比較が一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：１文字分後ろ側に移動
先頭の位置で比較が不一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：先頭に移動
先頭の位置 “以外” で比較が不一致した場合：
- テキストの比較位置：直前の比較で一致した文字数 - 1 文字数分前側に移動
- パターンの比較位置：先頭に移動

これに対比して考えると、KMP 法ではテキストの比較位置とパターンの比較位置は下記のように移動させながら比較を行います。

文字の比較が一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：１文字分後ろ側に移動
先頭相当の位置で比較が不一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：先頭に移動
先頭相当の位置 “以外” で比較が不一致した場合：
- テキストの比較位置：移動しない
- パターンの比較位置：“適切な位置” に移動

さらに、この “適切な位置” は “不一致した位置” と “パターンの文字列” から求めます。

“先頭” が “先頭相当” に変わっているのは、KMP 法では先頭の位置以外で文字が不一致した場合でも、下記のようにテキストの比較位置とパターンの比較位置を移動させる場合があるためです。

テキストの比較位置：１文字分後ろ側に移動
パターンの比較位置：先頭に移動

文字の不一致が発生した際に、上記のようにテキストの比較位置とパターンの比較位置を移動させる場合の不一致が発生した位置を “先頭相当” と呼んでいます。

これについては、連続して行われる同じ比較をスキップするで説明しますので、そこまでは “先頭相当 = 先頭” と解釈して考えていただいて問題ありません。

そう考えると、結局 KMP 法と力まかせ法の違いは「先頭の位置以外で比較が不一致した場合の “テキストの比較位置” と “パターンの比較位置” の移動先」のみとなります。

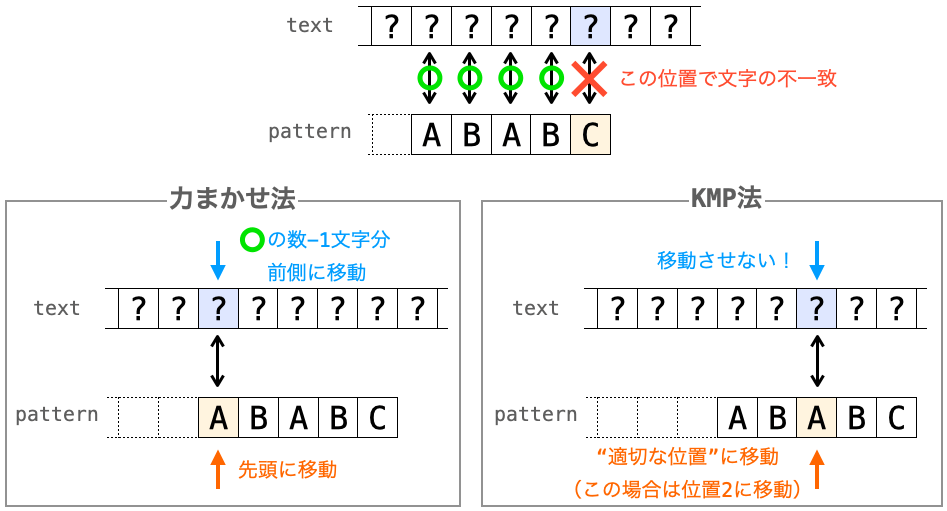
要は、KMP 法とは、先頭の位置以外で文字の比較が不一致した際にテキストの比較位置を前側に移動する代わりに、パターンの比較位置を “適切な位置” に移動するように “力まかせ法を改良した” 文字列検索アルゴリズムになります。

さらに上記のように考えると、KMP 法は力まかせ法に対して下記を変更することで実現することができます。

“適切な位置” を求めるように変更
文字の不一致時に “適切な位置” から比較を再開するように変更

もう少し具体的にいうと、実際に文字列の検索を行う処理としては、力まかせ法の復習で紹介した forceSearch 関数における “文字が不一致した場合の処理” を変更するのみで KMP 法を実装することができます。

ただ、KMP 法の説明を聞いて下記のように疑問を抱く方もおられるのではないでしょうか？

“適切な位置” って何？
テキストの比較位置が前に移動しないのに検索漏れは発生しないの？
なんでこれで検索効率が向上するの？
なぜ “不一致した位置” と “パターンの文字列” から “適切な位置” が求まるの？

私も KMP 法のプログラムや説明を見て、上記のような疑問を抱きました…。

同じような疑問を抱く方もおられると思いますので、次は KMP 法の実装方法ではなく、まずは KMP 法の仕組みについて解説し、上記の疑問の答えを説明していきたいと思います。

そして、その後に、KMP 法の実装方法の章で KMP 法の具体的な実装の仕方を解説していきたいと思います。

KMP 法の仕組み

では、この KMP 法で漏れなく検索を行われる仕組みを解説していきたいと思います。

“適切な位置” とは

まず KMP 法を理解する上で重要なのが “適切な位置” の意味です。

結論的には、”適切な位置” とは、力まかせ法で先頭以外の文字が不一致した際に行われる “テキストの比較位置が元に戻って来るまでの比較” の結果を再現するためのパターンの比較再開位置になります。

上記を分かりやすく説明するために、再度 “力まかせ法” での文字列検索時の動作を思い出したいと思います。

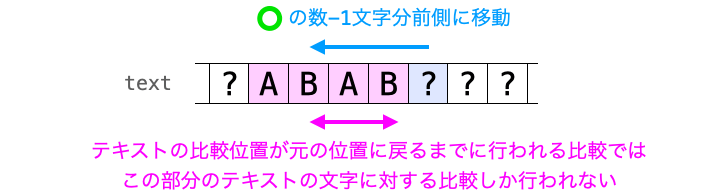
力まかせ法では、パターンの先頭以外の位置で文字が不一致した場合、テキストの比較位置は不一致が発生した時の位置から 直前の比較で一致した文字数 - 1 文字数分前側に移動することになります。

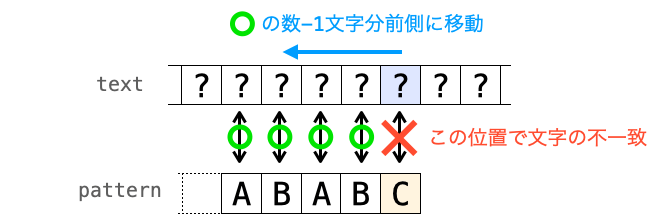
そして、テキストの比較位置が前側に移動した後に再度比較を行なっていくことになります。力まかせ法で比較を行なっていくので、要は下記のようにテキストの比較位置とパターンの比較位置を移動させながら比較を行なっていくことになります。

文字の比較が一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：１文字分後ろ側に移動
先頭の位置で比較が不一致した場合：
- テキストの比較位置：１文字分後ろ側に移動
- パターンの比較位置：先頭に移動
先頭の位置 “以外” で比較が不一致した場合：
- テキストの比較位置：直前の比較で一致した文字数 - 1 文字数分前側に移動
- パターンの比較位置：先頭に移動

で、この比較を繰り返し行っていけば、いずれは必ずテキストの比較位置が元々の位置（つまり先ほど文字の不一致が発生したときに比較していた位置）まで戻ってくることになります。

では、元々の位置にテキストの比較位置が戻ってきた時、最初に不一致が発生した時に比べてどのような点が変化しているでしょうか？

力まかせ法は前述の通りテキストの比較位置とパターンの比較位置の２つを移動させながら比較を行なっていく文字列検索アルゴリズムです。

ただし、テキストの比較位置は元々の位置に戻ってきたのですから当然変化はありません。

つまり、元々の位置にテキストの比較位置が戻ってきた時に変化しているのは “パターンの比較位置のみ” になります。

MEMO

この間の比較によってパターン全体が見つかっているということはあり得ません

先頭側から比較を行なっているため、最初に不一致が発生した時からテキストの比較位置が後ろ側に移動しない限り、パターン全体が見つかることはありません

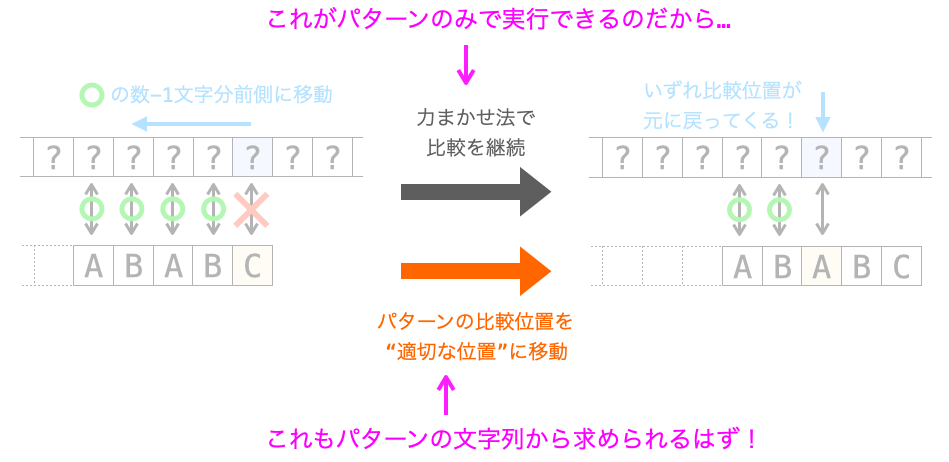
であれば、先頭以外の文字で不一致した際に “テキストの比較位置が元に戻って来るまでの比較” を行わなくても、パターンの比較位置さえ “適切な位置” に移動させてやれば、力まかせ法で “テキストの比較位置が元に戻って来るまでの比較” を実施した後の状態を再現することができます。

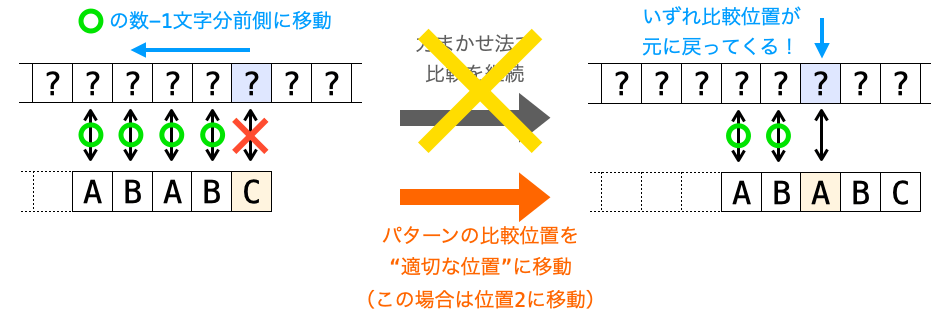
つまり、この “テキストの比較位置が元に戻って来るまでの比較” 実施後の状態を再現するための “パターンの比較位置” の移動先が、下記の KMP 法における “適切な位置” と考えることができます。

最初にざっくり説明しておくと、KMP 法とは「文字の比較が不一致した際に、その “不一致した位置” と “パターンの文字列” から求まる “適切な位置” から比較を再開することで効率的に検索を行う文字列検索アルゴリズム」です。

ここで１点補足しておきます。先ほどお見せした下の図を見て「テキストの比較位置が元に戻ってきたときに最初の２文字が一致しているけど、これは再現しなくていいの？」と疑問を抱かれた方もいらっしゃるのではないでしょうか？

この再現は必要です。ですが、この再現もパターンの比較位置の “適切な位置” への移動により実現することができます。

力まかせ法において、パターンの比較位置が後ろ側に移動するということは、その前側の位置の文字は一致していたことを意味します。

つまり、パターンの比較位置を “適切な位置” に移動するということは、”適切な位置” より前の文字が一致したことを再現することにもなります。

ですので、もし “適切な位置” からパターンの最後の文字まで比較が一致した場合、”適切な位置” までの比較はスキップされることになりますが、パターンは見つかったと判断することができます。

検索漏れが発生しない＆検索効率が向上する理由

前述の通り、パターンの比較位置を “適切な位置” に移動してやれば、力まかせ法で “テキストの比較位置が元に戻って来るまでの比較” を実施した後の状態を再現することができます。

つまり、パターンの比較位置の “適切な位置” への移動は、力まかせ法での “テキストの比較位置が元に戻って来るまでの比較” と同等の処理と考えられます。

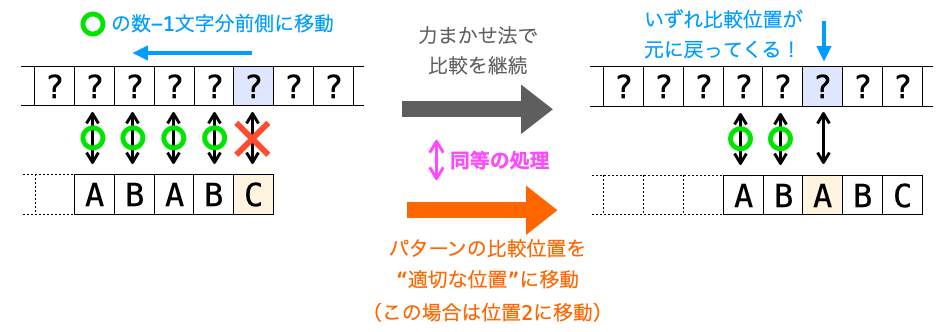
同等の処理なのであれば、その再現後に力まかせ法同様に比較を再開してやれば、力まかせ法と同じ検索結果を得ることができることになります。

さらに、力まかせ法がパターンを漏れなく検索することができるアルゴリズムであることを考慮すれば、KMP 法でもパターンを漏れなく検索することができると言えます。

また、力まかせ法では不可欠な “テキストの比較位置が元に戻って来るまでの比較” を、KMP 法ではパターンの比較位置を “適切な位置” に移動する処理に代替することができます。

つまり、KMP 法では “テキストの比較位置が元に戻って来るまでの比較” はスキップすることができます。

このスキップの分、力まかせ法よりも KMP 法の方が効率が良いことは直感的にも理解できると思います。

“パターンの文字列” と “不一致した位置” から “適切な位置” が求まる理由

前述の通り、パターンの比較位置を “適切な位置” に設定する理由は、力まかせ法で行われる “テキストの比較位置が元に戻って来るまでの比較” の結果を再現するためです。

なので、考え方としては、力まかせ法で “テキストの比較位置が元に戻って来るまでの比較” を実際に実行してみれば、この “適切な位置” を求めることができることになります。

ただ、”テキストの比較位置が元に戻って来るまでの比較” ではテキストの文字とパターンの文字の比較が行われます。となると、”適切な位置” を求めるためには “テキストの文字列” も必要な気がしますね…。

ですが、下記のことを考慮すると、”適切な位置” は “パターンの文字列” と “不一致した位置” のみから求めることが可能であることが分かります。

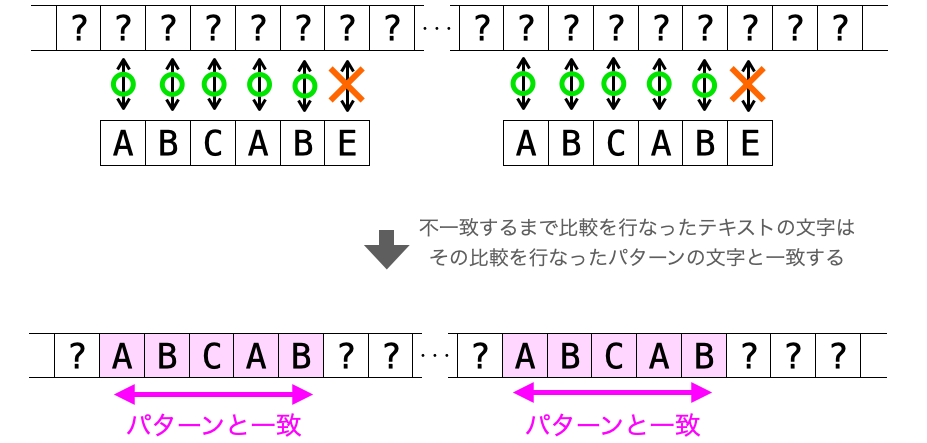
力まかせ法において、パターンのある位置で文字が不一致した場合、不一致するまでに比較されたテキストの文字はパターンの文字と一致する

力まかせ法ではパターンの先頭からテキストの文字を比較していきますので、パターンのある位置で文字が不一致したということは、それ以前にパターンと比較されたテキストの文字はパターンの文字と一致することになります。

さらに、”テキストの比較位置が元に戻って来るまでの比較” で比較が行われるテキストの文字は、直前の比較で “パターンの２文字目の文字〜パターンの不一致した位置の直前の文字” と比較したもののみです。

つまり、”テキストの比較位置が元に戻って来るまでの比較” で参照されるテキストの文字は、パターンの文字と一致してるもののみです。

ですので、わざわざテキストの文字列を参照しなくても、パターンの文字同士の比較によって “テキストの比較位置が元に戻って来るまでの比較” を実行することが可能です。

さらに前述の通り、力まかせ法で “テキストの比較位置が元に戻って来るまでの比較” を実際に実行してみれば、この “適切な位置” を求めることができます。ということは、”適切な位置” もパターンの文字列のみから求めることができますね！

これが、”パターンの文字列” から “適切な位置” が求められる理由になります。要は “適切な位置” を求めるのに “テキストの文字列” は不要ということです。

また、上記を考慮すれば、テキストの比較位置がどこであったとしても、パターンの “同じ位置” で文字が不一致した場合、その不一致する前に比較を行なったテキストの文字は同じであることになります。

ということは、テキストの比較位置がどこであったとしても、パターンの同じ位置で不一致した場合に行われる “テキストの比較位置が元に戻って来るまでの比較” は全く同じ文字列に対して比較を行なうことになります。

この場合、”テキストの比較位置が元に戻って来るまでの比較” も全く同じ処理になりますので、当然求まる “適切な位置” も同じになります。

つまり、パターンの同じ位置で文字が不一致した場合の “適切な位置” は、その不一致時のテキストの比較位置に関わらず全て同じ値となります。

これが “適切な位置” はパターンの “不一致した位置” から求めることができる理由です。

また、パターンの “不一致した位置” から “適切な位置” は求まるのですから、各位置で不一致した時の “適切な位置” を一度求めてそれを配列などに格納しておけば、あとは先頭以外の文字で不一致した際に、その位置に対応した “適切な位置” をその配列から取得するだけで文字列検索を行うことができるようになります。

さらに、”適切な位置” は “パターンの文字列” から求めることができるので、各位置で不一致した時の “適切な位置” は、文字列検索を実施する前に求めておくことができます。

したがって、実際に文字列検索を実施する際は、先頭以外の文字で不一致した時には「事前に求めておいた “適切な位置” を配列等から取得してパターンの比較位置を移動させる」のみを行えばよいことになります。

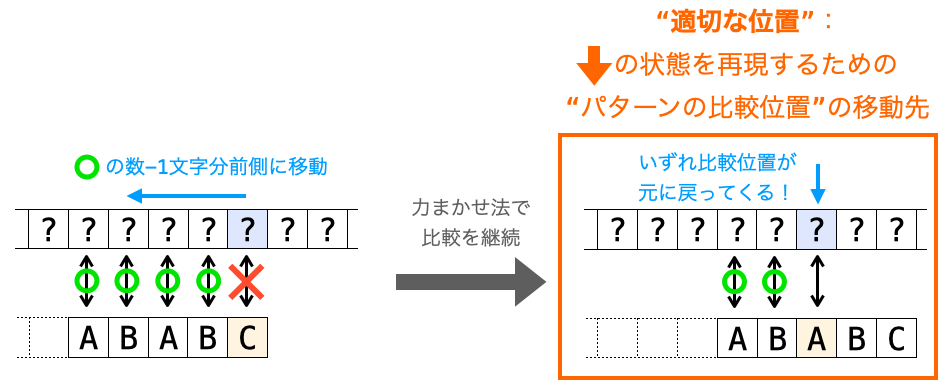
ここで１点補足しておきます。

この節では “適切な位置” を実際に力まかせ法を行って求めることを前提に解説しましたが、これはあくまでも “適切な位置” が “パターンの文字列” と “不一致した位置” から求められることを直感的に理解していただくためです。

この方法で “適切な位置” を求めると効率が悪いので、実際にはもっと効率の良い方法で “適切な位置” を求めることが要求されます。この効率の良い方法で求める方法については、次の “適切な位置” を求めるで解説します。

KMP 法の仕組みまとめ

ここまでの解説を、前述で挙げた KMP 法の疑問点に答える形でまとめておきたいと思います。

“適切な位置” って何？
- 力まかせ法で先頭以外の文字が不一致した際に行われる “テキストの比較位置が元に戻って来るまでの比較” の結果を再現するための “パターンの比較再開位置” です
テキストの比較位置が前に移動しないのに検索漏れは発生しないの？
- パターンの比較位置を “適切な位置” に移動することで “テキストの比較位置が元に戻って来るまでの比較” の結果を完全に再現することができるので検索漏れは発生しません
なんでこれで検索効率が向上するの？
- “テキストの比較位置が元に戻って来るまでの比較” をスキップすることが可能だからです
なぜ “パターンの文字” と “不一致した位置” から “適切な位置” が求まるの？
- パターンのある位置で文字が不一致した場合、不一致するまでに比較されたテキストの文字がパターンの文字と一致するからです

以上が、KMP 法の仕組みの解説になります。

KMP 法の実装方法

次は KMP 法の実装方法について解説していきます。

前述の通り、力まかせ法との違いは、KMP 法では下記を行う必要があるという点のみです。

“適切な位置” を求める
文字の不一致時に “適切な位置” から比較を再開する

ということで、ここでは上記の２点を実装する方法について解説していきます。

“適切な位置” を求める

では、まずは “適切な位置” を求めるための実装について解説していきたいと思います。念の為復習しておくと、”適切な位置” とは、パターンの先頭以外で文字が不一致した時のパターンの比較位置の移動先の位置です。

最悪力まかせ法で求めることもできる（効率悪い）

KMP 法の仕組みで解説した通り、文字が不一致した際にパターンの比較位置を “適切な位置” に移動するのは、力まかせ法で “テキストの比較位置が元に戻って来るまでの比較” を行なった結果を再現するためです。

逆に考えると、不一致した直後の状態から、力まかせ法で “テキストの比較位置が元に戻って来るまでの比較” を実際に実行すれば、上記を再現するための “適切な位置” を求めることができることになりますね！

また、“パターンの文字列” と “不一致した位置” から “適切な位置” が求まる理由で説明したように、”テキストの比較位置が元に戻って来るまでの比較” はテキストを使用しなくてもパターンの文字列のみから実行することが可能です。

この辺りを踏まえて作成した createNextTable 関数は下記のようになります。kmpNext に各位置で不一致した時の “適切な位置” を格納しています。

力まかせ法で適切な位置を求める

void createNextTable(int kmpNext[], char pattern[], int len) {

    int text_pos; /* テキストの比較位置 */
    int pattern_pos; /* パターンの比較位置*/
    int mis_pos; /* 不一致した位置 */

    /* 先頭の位置の適切な位置は-1にしておく */
    kmpNext[0] = -1;

    /* 各位置で不一致した時の適切な位置を求める */
    for (mis_pos = 1; mis_pos <= len; mis_pos++) {

        /* 不一致直後の状態を作る */

        /* パターンの比較位置を先頭にセット */
        pattern_pos = 0;

        /* 不一致直後のテキストの比較位置をセット
          (不一致した位置から、"それまでに一致した比較回数-1"分戻った位置) */
        text_pos = 1; /* mis_pos - (mis_pos - 1); */

        /* テキストの比較位置が不一致した時の位置に戻るまでループ */
        while (text_pos < mis_pos) {
            /* テキストの比較位置の文字とパターンの比較位置の文字が一致するかを判断 */
            if (pattern[text_pos] == pattern[pattern_pos]) {
                /* 一致した場合 */

                /* テキストとパターンの比較位置を１文字分後ろ側に移動する */
                text_pos++;
                pattern_pos++;

            } else {
                /* 不一致した場合 */

                /* 不一致した位置が先頭の位置であるかを判断 */
                if (pattern_pos == 0) {
                    /* 先頭の位置で比較が不一致した場合 */

                    /* テキストの比較位置を１文字分後ろ側に移動する */
                    text_pos++;

                    /* パターンの比較位置を先頭に移動する */
                    pattern_pos = 0;
                } else {
                    /* 先頭の位置以外で比較が不一致した場合 */

                    /* テキストの比較位置を前側に移動する */
                    text_pos -= (pattern_pos - 1);

                    /* パターンの比較位置を先頭に移動する */
                    pattern_pos = 0;
                }
            }
        }

        /* テキストの比較位置が元に戻ってきた時の
           パターンの比較位置を適切な位置とする */
        kmpNext[mis_pos] = pattern_pos;
    }
}

簡単に説明しておくと、基本的に mis_pos に対する for ループの内側の処理は力まかせ法と同じです（mis_pos は不一致位置を表す変数になります）。力まかせ法の復習で紹介した forceSearch 関数と比べれば、ほぼ同じことをやっていることが確認できると思います。

ただ、“パターンの文字列” と “不一致した位置” から “適切な位置” が求まる理由で説明したように “テキストの比較位置が元に戻って来るまでの比較” はパターンの文字列のみで実行することができるので、上記で行っている比較は全てパターンの文字同士によるものになります。

また、やりたいことは “テキストの比較位置が元に戻って来るまでの比較” なので、テキストの比較位置 text_pos が不一致位置 mis_pos まで移動した時点で力まかせ法による処理は終了しています。この時点で “テキストの比較位置が元に戻って来るまでの比較” を実行したことになるので、その時点のパターンの比較位置 pattern_pos が、mis_pos の位置で不一致した時の “適切な位置” になります。

“適切な位置” の意味を再度考えてみる

確かに上記の方法で “適切な位置” を求めることはできるのですが効率が悪いです。

もっと効率的に “適切な位置” を求める方法がないか考えてみましょう！

そのために、ここで “適切な位置” の意味合いについて深掘りしたいと思います。

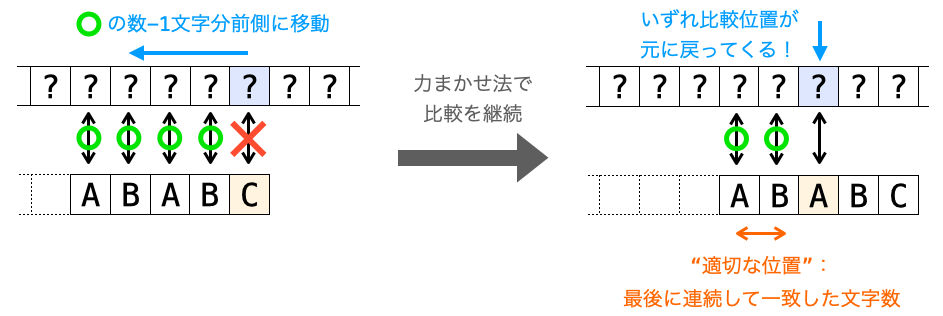
前述の通り、”適切な位置” は “テキストの比較位置が元に戻って来るまでの比較” 実行後の状態を再現するためのパターンの比較再開位置です。

また、力まかせ法において、パターンの比較位置が後ろに移動するということは、その前の文字の比較が一致したことを意味します。

上記の２つを合わせて考えると、”適切な位置” とは “テキストの比較位置が元に戻って来るまでの比較” で最後に連続して比較が一致した文字数であると考えることができます。

比較はパターンの先頭から行われていくわけですから、要は “適切な位置” 文字数分の文字が、パターンの先頭部分とテキストの文字が不一致した位置の直前部分で一致したことになります。

つまり、”適切な位置” とは、パターンにおける “先頭の文字から始まる文字列” とテキストにおける “文字が不一致した位置の直前の文字で終わる文字列” とで一致する文字数と考えることができます。

また、“パターンの文字列” と “不一致した位置” から “適切な位置” が求まる理由で説明したように、不一致した位置の前側のテキストの文字はパターンの文字と一致します。

これを考慮すれば、”適切な位置” とは、パターンの “先頭の文字から始まる文字列” とパターンの “文字が不一致した位置の直前の文字で終わる文字列” とで一致する文字数と考えることができます。

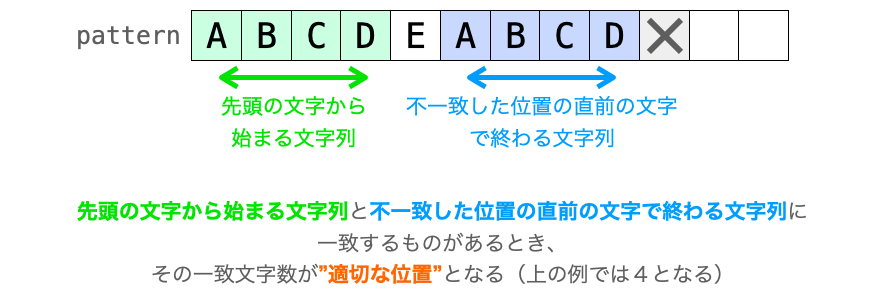
ここで、パターンの “先頭の文字から始まる文字列” と “文字が不一致した位置の直前の文字で終わる文字列” について補足しておきます。

まず、これらの文字列として当てはまるのは文字列長が “比較が不一致したパターンの位置未満” のもののみです（”適切な位置” は、必ず比較が不一致した位置よりも前の位置になるため）。

また、”先頭の文字から始まる文字列” と “文字が不一致した位置の直前の文字で終わる文字列” とで一致するものが複数存在する場合があります。

例えばパターンが "AABBAABBAAX" の場合、'X' の文字で不一致したと考えると、一致する文字列には下記の３つのものが存在することになります。

"AABBAA"
"AA"
"A"

このように一致する文字列が複数ある場合、一番長い文字列の文字数が “適切な位置” となります。

前側の位置の “適切な位置” を利用して効率的に求める

この考え方を利用すれば、効率的に “適切な位置” を求めることができます。より具体的には、前側の位置で不一致した時の “適切な位置” を利用することで効率的に “適切な位置” を求めることができます。

では、この方法について解説していきます。

ここでは各位置で不一致した場合の “適切な位置” を kmpNext 配列に格納していくものとして解説します。つまり、位置 i で不一致した場合の “適切な位置” を kmpNext[i] に格納します。

また、前側の位置で不一致した時の “適切な位置” を後から利用したいので、”適切な位置” はパターンの先頭の位置から順に求めていきます。

ということで、まずは先頭の位置（位置 0）の “適切な位置”、つまり kmpNext[0] から求めていきましょう！

といっても、KMP 法と力まかせ法の違いで解説したように、位置 0 で不一致した場合は力まかせ法同様の処理を行うことになります。なので、他の位置と区別できる値さえ設定すれば kmpNext[0] はなんでも良いのですが、一番都合が良いのは -1 です。なので、ここでも kmpNext[0] = -1 としたいと思います。

次は kmpNext[1] ですが、位置 1 の “適切な位置” は必ず 0 になります。これは先頭の文字の位置と、位置 1 の直前の文字の位置が同じだからです。

下記の条件があるため、この場合は “先頭の文字から始まる文字列” と “文字が不一致した位置の直前の文字で終わる文字列” として当てはまるものが存在しないことになります。

なので、kmpNext[1] = 0 となります。

まず、これらの文字列として当てはまるのは文字列長が “比較が不一致したパターンの位置未満” のもののみです（”適切な位置” は、必ず比較が不一致した位置よりも前の位置になるため）。

次は、位置 i で比較が不一致した時の “適切な位置”、つまり kmpNext[i] を求めることを考えていきます（i は 2 〜 パターンの文字数 の値を取る変数です）。

先頭側から kmpNext の値が格納されていっているので、この kmpNext[i] の値を求める時点で、位置 kmpNext[0] 〜 kmpNext[i - 1] の値は既に格納済みであることになります。

ここで kmpNext[i - 1] の値に注目すると、これは位置 i - 1 で文字が不一致した時の “適切な位置” です。で、これは前述の通り、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” の一致文字数です。

ここで kmpNext[i - 1] の値を j とすると、上記はパターンの第 0 文字〜第 j - 1 文字と第 i - j - 1 文字〜第 i - 2 文字が一致していることを意味することになります。

ということは、もし第 j 文字と第 i - 1 文字が一致すれば、”先頭の文字から始まる文字列” と “位置 i の直前の文字で終わる文字列” の一致文字数は j + 1 文字であると考えることができます。

つまりこの場合、kmpNext[i] = j + 1 ということになり、位置 i に対する “適切な位置” が求まったことになります。

その一方で、第 j 文字と第 i - 1 文字が一致しない場合は kmpNext[i] をどうやって求めれば良いでしょうか？

先程はパターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” として文字数が j のものを用いました。

ただ、”先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” としてもっと文字数の短い文字列が存在する可能性があります。

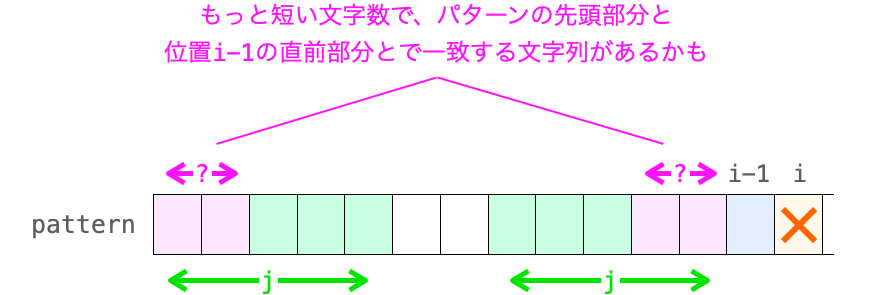
もしこれが存在するのであれば、その文字列の文字数を “新たな j” として先ほどと同様に下記を行えば kmpNext[i] を求めることができそうです。

もし第 j 文字と第 i - 1 文字が一致すれば、”先頭の文字から始まる文字列” と “位置 i の直前の文字で終わる文字列” の一致文字数は j + 1 文字であると考えることができます。

つまりこの場合、kmpNext[i] = j + 1 ということになり、位置 i に対する “適切な位置” が求まったことになります。

つまり、第 j 文字と第 i - 1 文字が一致するかを確認し、もし一致する場合は kmpNext[i] = j + 1 とすることができます。

ということは、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” が一致する文字列として、”j よりも短い文字列” の文字数を求めることができれば、kmpNext[i] の値を簡単に求めることができることになります。

これを求めるために注目したいのが、パターンの先頭側の j 文字の文字列です。

まずここで、 kmpNext[j] がどのような値であるかを思い出してみましょう。

この kmpNext[j] は、パターンの “先頭の文字から始まる文字列” と “位置 j の直前の文字で終わる文字列” の一致文字数ですね！

つまり、この j 文字の文字列において、先頭側と末尾側とで kmpNext[j] 文字が一致することになります。

また、kmpNext[i - 1] == j であることを考慮すると、この j 文字の文字列がパターンの “先頭の文字から始まる文字列” であるということは、”位置 i - 1 の直前の文字で終わる文字列” でもあることになります。

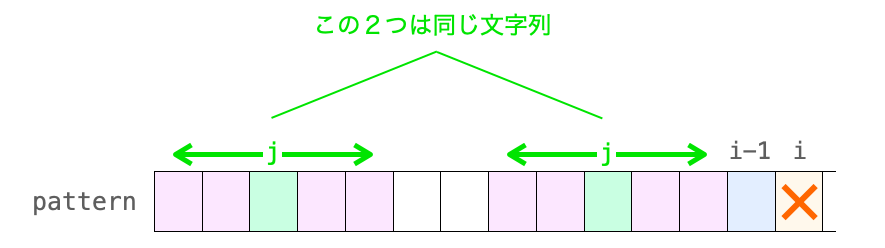
さらに、この j 文字の文字列の先頭側と末尾側が kmpNext[j] 文字分一致するということは、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” でも kmpNext[j] 文字分一致することになります。

つまり、kmpNext[j] は、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” が一致する文字列として、”j よりも短い文字列” の文字数になります。

ですので、kmpNext[i] を求める際に、第 j 文字と第 i - 1 文字が一致しない場合、次は、j = kmpNext[j] としてから、同様に第 j 文字と第 i - 1 文字を比較すれば良いことになります。で、一致していれば kmpNext[i] = j + 1 となります。

もしここでも第 j 文字と第 i - 1 文字が一致しない場合は、再度 j = kmpNext[j] としてから同様のことを行えば良いです。これを繰り返すことにより、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” が一致するものとして、”j よりも短い文字列” の文字数をどんどん更新しながら比較を行なっていくことができます。

もし j が 0 になった場合は、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” が一致する文字列として、”j よりも短い文字列” が存在しないということになります。

この場合は、単にパターンの第 0 文字とパターンの第 i - 1 を比較し、一致していれば 1 を、不一致した場合は 0 を格納することになります（これも j = 0 として考えれば今までの処理と同様の処理として捉えることができます）。

以上の処理により kmpNext[i]、つまりパターンの “先頭の文字から始まる文字列” と “位置 i の直前の文字で終わる文字列” の一致文字数、さらに言い換えれば位置 i で文字が不一致しときの “適切な位置” を求めることができます。

ちょっと説明が長くなったので簡単にまとめておくと、パターンの “先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” の一致文字数が j である場合、パターンの第 j 文字とパターンの第 i - 1 文字が一致するのであれば kmpNext[i] = j + 1 となります。

一致しない場合は、j = kmpNext[j] として同様の比較を繰り返し行います。

ここまでの解説を踏まえて作成した createNextTable 関数は下記のようになります。

createNextTable(1)

void createNextTable(int kmpNext[], char pattern[], int len) {

    int i, j;

    kmpNext[0] = -1;
    kmpNext[1] = 0;
    
    /* 位置2以降で文字が不一致した場合の"適切な位置"を求める */
    for (i = 2; i <= len; i++) {

        /* 直前の位置のkmpNextを取得 */
        j = kmpNext[i - 1];

        /* より短い一致文字数を探して比較 */
        while (j > 0 && pattern[i - 1] != pattern[j]) {
            /* １段階短い一致文字数を取得 */
            j = kmpNext[j];
        }

        /* ここまで処理が進んだということは、
           pattern[i-1]とpattern[j]が一致した or
           もうこれ以上短い一致文字数が見つからない（j==0）*/

        if (pattern[i - 1] == pattern[j]) {
            /* pattern[i-1]とpattern[j]とが一致した場合は単に+1 */
            j++;
        }

        /* 位置iに対する"適切な位置"をjに設定 */
        kmpNext[i] = j;
    }
}

この createNextTable は、引数 pattern で与えられるパターンに対し、各文字で文字が不一致した場合の “適切な位置” を kmpNext に格納する関数です。パターンの長さは引数 len で与えられることを想定しています。

ポイントは下記の while ループの部分です。

kmpNextを辿る処理

/* より短い一致文字数を探して比較 */
while (j > 0 && pattern[i - 1] != pattern[j]) {
    /* １段階短い一致文字数を取得 */
    j = kmpNext[j];
}

もしパターンの第 j 文字と第 i - 1 文字が一致する場合は、この while ループは即座に抜け出して、次の if 文の中で j++ されます。

文字が一致した時の処理

if (pattern[i - 1] == pattern[j]) {
    /* pattern[i-1]とpattern[j]とが一致した場合は単に+1 */
    j++;
}

一致しない場合は、上記の while ループの中で j = kmpNext[j] を実行し、”先頭の文字から始まる文字列” と “位置 i - 1 の直前の文字で終わる文字列” の一致文字数 j を１段階ずつ減らししながらパターンの第 j 文字と第 i - 1 文字を比較していっています。

パターンの第 j 文字と第 i - 1 文字で一致した、もしくは j が 0 になった場合は while ループを抜け出し、次の if 文の中で再度パターンの第 j 文字と第 i - 1 文字を比較し、一致する場合は j++ しています。

もし、パターンの第 j 文字と第 i - 1 文字で一致するかの比較が while ループでも if 文でも行われていて気持ち悪いという場合は、createNextTable 関数を下記のように変更することで改善することができます。

createNextTable(2)

void createNextTable(int kmpNext[], char pattern[], int len) {

    int i, j;

    kmpNext[0] = -1;

    /* 位置1以降で文字が不一致した場合の"適切な位置"を求める */
    for (i = 1; i <= len; i++) {

        /* 直前の位置のkmpNextを取得 */
        j = kmpNext[i - 1];

        /* より短い一致文字数を探して比較 */
        while (j >= 0 && pattern[i - 1] != pattern[j]) {
            /* １段階短い一致文字数を取得 */
            j = kmpNext[j];
        }

        /* ここまで処理が進んだということは、
           pattern[i-1]とpattern[j]が一致した or j==-1
           なので、いずれにせよ+1すればよい */
        j++;

        /* 位置iに対する"適切な位置"をjに設定 */
        kmpNext[i] = j;
    }
}

この場合、while ループを抜け出すのは “パターンの第 j 文字と第 i - 1 文字で一致した場合” と “j が -1 になった場合” になります。

前者の場合は前述の解説の通り j++ されて “適切な位置” として設定されます。後者の場合は j++ することで j が 0 になるので、”適切な位置” として辻褄が合った値になります（ただしこれが成立するのは kmpNext[0] が -1 の場合のみです）。

また、kmpNext[1] も必ず 0 になるので、ループは i = 1 から始められます。

また、この createNextTable は下記のように書き換えても正常に動作します。

createNextTable(3)

void createNextTable(int kmpNext[], char pattern[], int len) {

    int i, j;

    kmpNext[0] = -1;

    /* jをkmpNext[1-1]で初期化 */
    j = kmpNext[0];
    
    /* 位置1以降で文字が不一致した場合の"適切な位置"を求める */
    for (i = 1; i <= len; i++) {

        /* より短い一致文字数を探して比較 */
        while (j >= 0 && pattern[i - 1] != pattern[j]) {
            /* １段階短い一致文字数を取得 */
            j = kmpNext[j];
        }

        /* ここまで処理が進んだということは、
           pattern[i-1]とpattern[j]が一致した or j==-1
           なので、いずれにせよ+1すればよい */
        j++;

        /* 位置iに対する"適切な位置"をjに設定 */
        kmpNext[i] = j;
    }
}

先に示した createNextTable では、i に対するループの最後で kmpNext[i] = j を行なっているので、次の週の最初の時点で必ず kmpNext[i - 1] == j となります。

なので、ループに入る前に、kmpNext[0] の値さえ j に設定しておけば、ループの最初の j = kmpNext[i - 1]; は不要になります。kmpNext[0] の値を j に設定するのは、ループが i = 1 から始まるためです（位置 1 の直前の位置の kmpNext の値を j に設定すればいい）。

また、上記のいずれの createNextTable 関数でも、パターンの文字数である len の位置に対しても “適切な位置” を求めていますが、これはミスではないです。

パターンを見つけた後も検索を続けたい場合は、パターンを見つけた直後にパターンの比較位置を “適切な位置” に移動する必要があります。その際の “適切な位置” が kmpNext[len] となります。

パターンが見つかったということは、パターンの第 len - 1 文字との比較が一致したことになります。もしその後も比較を行うのであれば、パターンの第 len 文字と比較が行われることになりますが、そのような文字は存在しないため必ず比較が不一致することになります。

なので、パターンを見つけた直後は比較を続けることなく、パターンの第 len 文字の位置で不一致したと考えて、パターンの比較位置を kmpNext[len] に移動すれば良いことになります。

このような動作を行えるようにするために、kmpNext[len] まで求めるようにしています。

最初のパターンのみを見つければ良いのであれば、len - 1 の位置までのみ “適切な位置” を求めてやるのでも問題ないはずです。

連続して行われる同じ比較をスキップする

実は、上記の createNextTable 関数は、正確には KMP 法のものではなく、MP 法によるものです。

詳細は下記ページで解説されています。

ここまで解説してきた内容で実装してしまうと、実はまだ無駄な比較が行われてしまいます。ここでは、この無駄な比較がどのような場合に発生するかを説明し、それをどのように改善すれば良いのかについて解説していきます。おそらくこの改善が、KMP 法の K の部分になると思います。

では早速、どのような場合に無駄な比較が発生してしまうのかについて説明していきます。

この無駄な比較が発生してしまう場合のパターンの具体例は pattern = "ABCDABCX" です。

このパターンにおいて、各文字の位置で比較が不一致した場合の “適切な位置” は下記のようになります（- は -1 を示しています）。

ABCDABCX
-0000123

例えば後ろ側の 'C' の位置で不一致した場合、”適切な位置” は 2 ですので、次はパターンの位置 2 から比較が再開されることになります（パターンの先頭を位置 0 として考えています）。

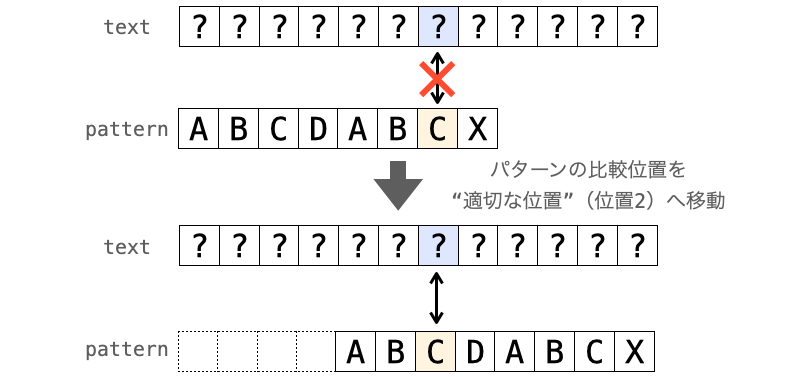
ただ、ここから比較を再開して意味があるでしょうか？

ここで不一致が発生したのは 'C' の文字です。そして、比較が再開されて最初に比較されるのも 'C' の文字です。絶対に比較は一致しませんよね…。

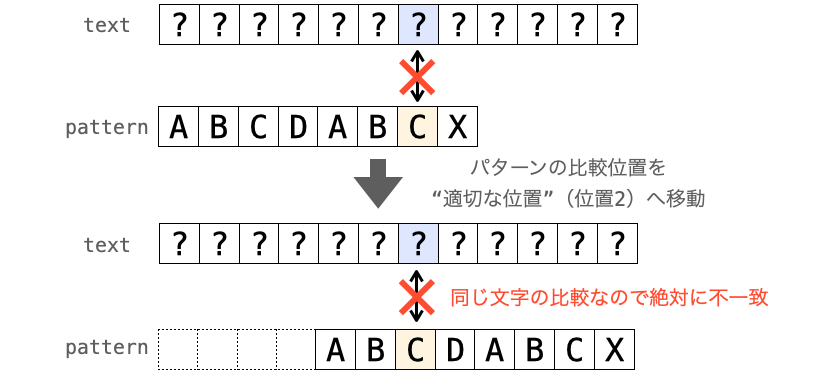
なので、直ちに前側の 'C' で不一致し、続いてパターンの位置 0 から比較が再開されることになります（前側の 'C' に対する “適切な位置” が 0 のため）。

つまり、１回目の 'C' との比較と２回目の 'C' との比較で連続して同じ比較が行われることになります。同じ比較なので同じ結果になるのは当然です。

なのであれば、最初に 'C' との比較で不一致が発生した時に、前側の 'C' に対する “適切な位置” に従って比較を再開しても問題ないですし、無駄な比較が行われなくて効率が向上します。

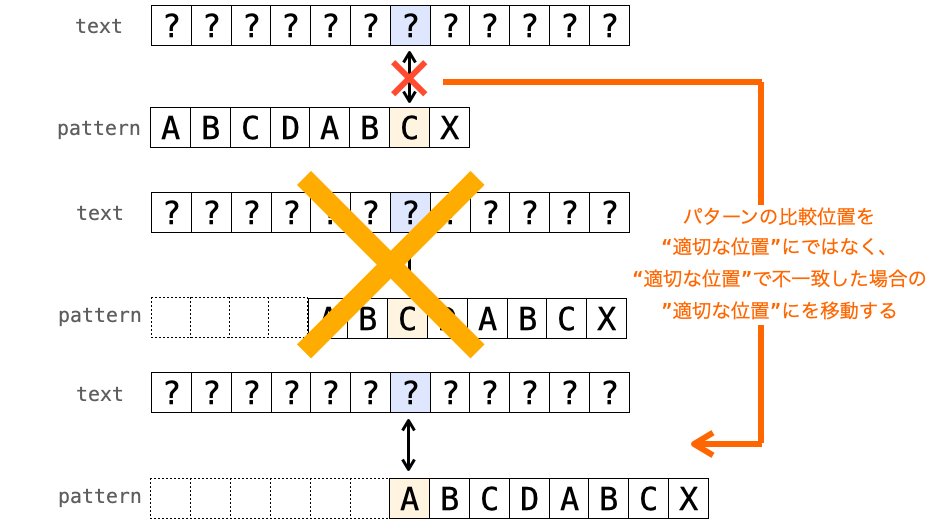
つまり、”不一致が発生した位置” の文字と、その位置で不一致が発生した時の “適切な位置” の文字が同じである場合、その比較は不一致になることが明白で、この比較は無駄です。

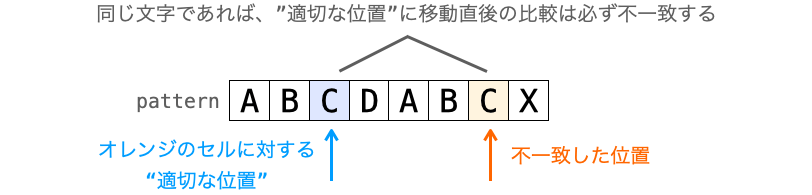
このような場合は、その不一致が発生した位置に対する “適切な位置” として、その “適切な位置” で不一致が発生した時の “適切な位置” を設定してやることで無駄な比較をスキップすることができます。

MEMO

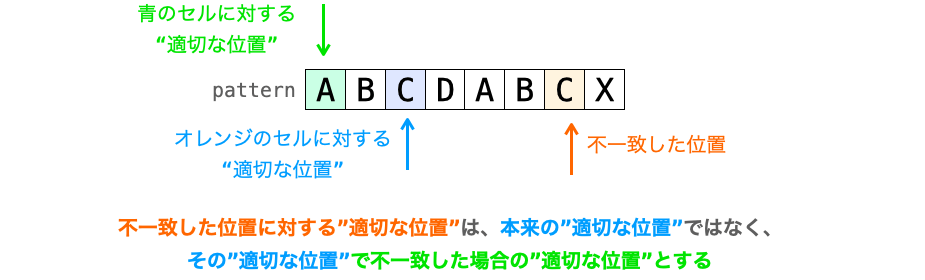
変数名を使用した方が理解しやすいかもしれません

不一致が発生した位置を X、その位置で不一致が発生した時の元々の “適切な位置” を Y、さらに各位置で比較が発生した時の “適切な位置” が配列 kmpNext に格納されているとすると、kmpNext[X] を Y ではなく kmpNext[Y] として設定することでこの無駄な比較をスキップすることができます。

このように “適切な位置” を設定するようにすれば、各文字の位置で比較が不一致した場合の “適切な位置” は下記のように変わります。

ABCDABCX
-000-003

この結果からも分かるように、この処理を行うことで下記の関係性が崩れることに注意してください。

“適切な位置” = パターンの”先頭の文字から始まる文字列” と “文字が不一致した位置の直前の文字で終わる文字列” の一致文字数

また、”適切な位置” が -1 になるものがパターンの先頭以外にも現れるようになります。つまり、先頭以外の位置で文字が不一致した際にも、力まかせ法同様の処理を行う場合が出てくるということになります。

これらの位置が KMP 法と力まかせ法の違いで登場した “先頭相当の位置” になります。

先頭相当の位置であるかどうかは、その位置の kmpNext の値が kmpNext[0] の値と同じであるかどうかで判断することが可能です（これは次の文字の不一致時に “適切な位置” から比較を再開するで利用します）。

以上を踏まえて変更した createNextTable 関数が下記のようになります。

createNextTable(4)

void createNextTable(int kmpNext[], char pattern[], int len) {

    int i, j;

    kmpNext[0] = -1;
    kmpNext[1] = 0;
    
    /* 位置2以降で文字が不一致した場合の"適切な位置"を求める */
    for (i = 2; i <= len; i++) {

        /* 直前の位置のkmpNextを取得 */
        j = kmpNext[i - 1];

        /* より短い一致文字数を探して比較 */
        while (j > 0 && pattern[i - 1] != pattern[j]) {
            /* １段階短い一致文字数を取得 */
            j = kmpNext[j];
        }

        /* ここまで処理が進んだということは、
           pattern[i-1]とpattern[j]が一致した or
           もうこれ以上短い一致文字数が見つからない（j==0）*/

        if (pattern[i - 1] == pattern[j]) {
            /* pattern[i-1]とpattern[j]とが一致した場合は単に+1 */
            j++;
        }

        /* 位置iに対する"適切な位置"をjに設定 */
        kmpNext[i] = j;
    }

    /* 連続して行われる同じ比較をスキップするための調整 */
    for (i = 0; i <= len; i++) {

        /* パターンの比較位置が"適切な位置"に移動すると
           連続して同じ比較が実行されてしまうかどうかを判断 */
        if (pattern[i] == pattern[kmpNext[i]]) {
            /* 実行されてしまう場合、その比較をスキップする */
            kmpNext[i] = kmpNext[kmpNext[i]];
        }
    }
}

前側の位置の “適切な位置” を利用して効率的に求めるで紹介した createNextTable 関数の後ろ部分に、”不一致が発生した位置” の文字と、その位置で不一致が発生した時の “適切な位置” の文字が同じである場合に “適切な位置” を上書きするための処理を追加しただけです。

ループをもし１つにしたい場合は下記のように書き換えることもできます。

createNextTable(5)

void createNextTable(int kmpNext[], char pattern[], int len) {

    int i, j;

    kmpNext[0] = -1;

    /* jをkmpNext[1-1]で初期化 */
    j = kmpNext[0];
    
    /* 位置1以降で文字が不一致した場合の"適切な位置"を求める */
    for (i = 1; i <= len; i++) {

        /* より短い一致文字数を探して比較 */
        while (j >= 0 && pattern[i - 1] != pattern[j]) {
            /* １段階短い一致文字数を取得 */
            j = kmpNext[j];
        }

        /* ここまで処理が進んだということは、
           pattern[i-1]とpattern[j]が一致した or j==-1
           なので、いずれにせよ+1すればよい */

        j++;

        /* パターンの比較位置が"適切な位置"に移動すると
           連続して同じ比較が実行されてしまうかどうかを判断 */
        if (pattern[i] == pattern[j]) {
            /* 実行されてしまう場合、その比較をスキップ*/
            kmpNext[i] = kmpNext[j];
        } else {
            /* 実行されない場合はそのままjを設定 */
            kmpNext[i] = j;
        }
    }
}

以上で、各位置で文字が不一致した場合の “適切な位置” を求めるための実装の解説は終了です。あとは、文字が不一致した時に “適切な位置” から比較を再開するように検索する処理を実装してやれば、KMP 法での文字列検索プログラムが完成します！

文字の不一致時に “適切な位置” から比較を再開する

“適切な位置” が求められたので、あとは文字の不一致時、もっと具体的に言えば先頭相当の文字の不一致時にパターンの比較位置を求めた “適切な位置” に移動させるようにして文字列検索を行えば良いだけです（さらにはテキストの比較位置は動かさないようにすれば良い）。

また、連続して行われる同じ比較をスキップするで説明した通り、先頭相当の位置であるかどうかはその位置の kmpNext の値が kmpNext[0] と一致しているかどうかで判断することができます。

力まかせ法の復習で紹介した forceSearch 関数をベースにすれば、以上を踏まえた KMP 法による文字列検索関数 kmpSearch は下記のようになります。

kmpSearch(1)

int kmpSearch(char text[], int text_len, char pattern[], int pattern_len) {

    int text_pos; /* テキストの比較位置 */
    int pattern_pos; /* パターンの比較位置*/
    int kmpNext[MAX_PATTERN]; /* 各位置で不一致した場合の"適切な位置"を格納する配列 */

    /* 各位置で不一致した場合の"適切な位置"を求める */
    createNextTable(kmpNext, pattern, pattern_len);

    /* パターンの比較位置を先頭にセット */
    pattern_pos = 0;

    /* テキストの比較位置を先頭にセット */
    text_pos = 0;

    /* テキストの比較位置がテキストの最後を超えるまでループ */
    while (text_pos < text_len) {
        /* テキストの比較位置の文字とパターンの比較位置の文字が一致するかを判断 */
        if (text[text_pos] == pattern[pattern_pos]) {
            /* 一致した場合 */

            /* パターンの最後の文字までテキストの文字が一致したかどうかを判断 */
            if (pattern_pos == pattern_len - 1) {

                /* パターンが存在する位置を返却 */
                return text_pos - pattern_pos; 
            }

            /* テキストとパターンの比較位置を１文字分後ろ側に移動する */
            text_pos++;
            pattern_pos++;

        } else {
            /* 不一致した場合 */

            /* 不一致した位置が先頭相当の位置であるかを判断 */
            if (kmpNext[pattern_pos] == kmpNext[0]) {
                /* 先頭相当の位置で比較が不一致した場合 */

                /* テキストの比較位置を１文字分後ろ側に移動する */
                text_pos++;

                /* パターンの比較位置を先頭に移動する */
                pattern_pos = 0;
            } else {
                /* 先頭相当の位置以外で比較が不一致した場合 */

                /* テキストの比較位置は移動しない */

                /* パターンの比較位置を"適切な位置"に移動する */
                pattern_pos = kmpNext[pattern_pos];
            }
        }
    }

    /* パターンが存在しなかった場合 */
    return -1;
}

forceSearch 関数との違いは（関数名と）文字が不一致した場合の処理のみです。

先頭相当以外の文字で不一致した場合に、pattern_pos を kmpNext[pattern_pos] に設定しているところがポイントです。これによりパターンの比較位置が “適切な位置” に移動します。

また、text_pos に対する引き算がなくなったので、テキストの比較位置が前側に移動しなくなったところも確認できると思います。

上記の kmpSearch では、パターンが見つかった際に最初に見つけたパターンが存在する位置を返却するようにしています。

もしパターンが見つかった後も文字列検索を継続したい場合は、パターンが見つかった際の return 部分を消し、代わりに下記を記述すれば良いです。

パターンが見つかった後も検索を継続する

/* パターンが存在する位置を表示 */
printf("%d\n", text_pos - pattern_pos);

/* 次の文字で比較に失敗するとみなして比較位置を移動 */
text_pos++;
pattern_pos = kmpNext[pattern_len];
continue;

これを行うためには kmpNext[pattern_len] も事前に求めておく必要がある点に注意してください（“適切な位置” を求めるで紹介した createNextTable 関数では全てこの kmpNext[pattern_len] も求めるようにしています）。

パターンが見つかった後もパターンの検索が継続されるので、パターンの全検索を行うようなこともできます。

また、上記の kmpSearch は次のように書き換えることもできます。

kmpSearch(2)

int kmpSearch(char text[], int text_len, char pattern[], int pattern_len) {

    int text_pos; /* テキストの比較位置 */
    int pattern_pos; /* パターンの比較位置*/
    int kmpNext[MAX_PATTERN]; /* 各位置で不一致した場合の"適切な位置"を格納する配列 */

    /* 各位置で不一致した場合の"適切な位置"を求める */
    createNextTable(kmpNext, pattern, pattern_len);

    /* パターンの比較位置を先頭にセット */
    pattern_pos = 0;

    /* テキストの比較位置を先頭にセット */
    text_pos = 0;

    /* テキストの比較位置がテキストの最後を超えるまでループ */
    for (text_pos = 0; text_pos < text_len; text_pos++) {

        /* テキストの比較位置が後ろ側に移動する条件を満たすまでループ */
        while (
            pattern_pos != kmpNext[0] &&
            text[text_pos] != pattern[pattern_pos]
        ) {
            /* パターンの比較位置を"適切な位置"に移動 */
            pattern_pos = kmpNext[pattern_pos];
        }
        
        /* パターンの最後の文字までテキストの文字が一致したかどうかを判断 */
        if (pattern_pos == pattern_len - 1) {

            /* パターンが存在する位置を返却 */
            return text_pos - pattern_pos;    
        }

        /* ここまで処理が進んだということは、
           テキストとパターンの文字が一致した or pattern_pos==-1
           なので、いずれにせよpattern_posを+1すれば良い */
        pattern_pos++;
    }

    /* パターンが存在しなかった場合 */
    return -1;
}

内側の while では、テキストの比較位置が１文字分後ろ側に移動する条件を満たすまでループが繰り返されることになります。つまり、先頭相当の文字で文字が不一致 or パターンの文字と一致するまでループが繰り返されます。

ループの中ではパターンの比較位置を “適切な位置” に移動させる処理を行なっていますので、いずれは上記条件を満たすことになります。

while ループを抜けた際には必ずテキストの比較位置が１文字分後ろ側に移動することになるので、for 文でテキストの比較位置をインクリメントしながら KMP 法による文字列検索を行うことができます。このように記述することで、テキストの比較位置が線形的に移動していることが分かりやすくなったと思います。

また、上記において、パターンが見つかった後も文字列検索を継続したい場合は、パターンが見つかった際の return 部分を消し、代わりに下記を記述すれば良いです。

パターンが見つかった後も検索を継続する

/* パターンが存在する位置を表示 */
printf("%d\n", text_pos - pattern_pos);

/* 次の文字で比較に失敗するとみなして比較位置を移動 */
pattern_pos = kmpNext[pattern_len];
continue;

先程の例の時とほぼ同様ですが、text_pos は for 文により +1 されるので、ここで text_pos++ を行う必要はありません。

最終的な KMP 法の文字列検索プログラム

ここまでの解説内容を全て踏まえて作成した KMP 法の文字列検索プログラムのソースコードは下記のようになります。

createNextTable と kmpSearch はここまで紹介してきた中で一番考え方がシンプルなものを利用しています。

kmp法

#include <stdio.h>
#include <string.h> /* strlen */

#define MAX_PATTERN 256
#define MAX_TEXT 1024

/*
 * patternの各位置で文字が不一致した場合の”適切な位置"を求めてkmpNextに格納する
 *
 * kmpNext："適切な位置"を格納する配列
 * pattern：適切な位置を求める対象のパターン
 * len：パターンの文字数
 * 
 */
void createNextTable(int kmpNext[], char pattern[], int len) {

    int i, j;

    kmpNext[0] = -1;
    kmpNext[1] = 0;
    
    /* 位置2以降で文字が不一致した場合の"適切な位置"を求める */
    for (i = 2; i <= len; i++) {

        /* 直前の位置のkmpNextを取得 */
        j = kmpNext[i - 1];

        /* より短い一致文字数を探して比較 */
        while (j > 0 && pattern[i - 1] != pattern[j]) {
            /* １段階短い一致文字数を取得 */
            j = kmpNext[j];
        }

        /* ここまで処理が進んだということは、
           pattern[i-1]とpattern[j]が一致した or
           もうこれ以上短い一致文字数が見つからない（j==0）*/

        if (pattern[i - 1] == pattern[j]) {
            /* pattern[i-1]とpattern[j]とが一致した場合は単に+1 */
            j++;
        }

        /* 位置iに対する"適切な位置"をjに設定 */
        kmpNext[i] = j;
    }

    /* 連続して行われる同じ比較をスキップするための調整 */
    for (i = 0; i <= len; i++) {

        /* パターンの比較位置が"適切な位置"に移動すると
           連続して同じ比較が実行されてしまうかどうかを判断 */
        if (pattern[i] == pattern[kmpNext[i]]) {
            /* 実行されてしまう場合、その比較をスキップする */
            kmpNext[i] = kmpNext[kmpNext[i]];
        }
    }
}

/*
 * KMP法によりtextからpatternを見つけ出す
 * 
 * text：テキストの文字列
 * text_len：テキストの文字数
 * pattern：パターンの文字列
 * pattern_len：パターンの文字数
 * 戻り値：パターンが見つかった場合はその位置、パターンが見つからない場合は-1
 */
int kmpSearch(char text[], int text_len, char pattern[], int pattern_len) {

    int text_pos; /* テキストの比較位置 */
    int pattern_pos; /* パターンの比較位置*/
    int kmpNext[MAX_PATTERN]; /* 各位置で不一致した場合の"適切な位置"を格納する配列 */

    /* 各位置で不一致した場合の"適切な位置"を求める */
    createNextTable(kmpNext, pattern, pattern_len);

    /* パターンの比較位置を先頭にセット */
    pattern_pos = 0;

    /* テキストの比較位置を先頭にセット */
    text_pos = 0;

    /* テキストの比較位置がテキストの最後を超えるまでループ */
    while (text_pos < text_len) {
        /* テキストの比較位置の文字とパターンの比較位置の文字が一致するかを判断 */
        if (text[text_pos] == pattern[pattern_pos]) {
            /* 一致した場合 */

            /* パターンの最後の文字までテキストの文字が一致したかどうかを判断 */
            if (pattern_pos == pattern_len - 1) {

                /* パターンが存在する位置を返却 */
                return text_pos - pattern_pos; 
            }

            /* テキストとパターンの比較位置を１文字分後ろ側に移動する */
            text_pos++;
            pattern_pos++;

        } else {
            /* 不一致した場合 */

            /* 不一致した位置が先頭相当の位置であるかを判断 */
            if (kmpNext[pattern_pos] == kmpNext[0]) {
                /* 先頭相当の位置で比較が不一致した場合 */

                /* テキストの比較位置を１文字分後ろ側に移動する */
                text_pos++;

                /* パターンの比較位置を先頭に移動する */
                pattern_pos = 0;
            } else {
                /* 先頭相当の位置以外で比較が不一致した場合 */

                /* テキストの比較位置は移動しない */

                /* パターンの比較位置を"適切な位置"に移動する */
                pattern_pos = kmpNext[pattern_pos];
            }
        }
    }

    /* パターンが存在しなかった場合 */
    return -1;
}

int main(void) {
    char text[MAX_TEXT] =  "baabaababaabaavaabaabaa";
    char pattern[MAX_PATTERN] = "aabaabaa";
    int find;

    find = kmpSearch(text, strlen(text), pattern, strlen(pattern));
    if (find != -1) {
        printf("パターンはテキストの第%d文字に存在します\n", find);
    } else {
        printf("パターンはテキスト内に存在しません...\n");
    }

    return 0;
}

main 関数でテキストとパターンの文字列の設定を行なっていますので、この辺りを変更すればファイルからテキストを読み込んだり、パターンをコマンド引数で受け取るようなことも可能です。

KMP 法の計算量

最後に KMP 法の計算量について解説しておきます。

テキストの文字数を M、パターンの文字数を N とすると、KMP 法の最悪計算量は、オーダー表記で O(M + N) となります。

実際の検索時の計算量が O(M) で、”適切な位置” を求める際の計算量が O(N) になります。

力まかせ法の最悪計算量は O(MN) なので、かなり高速になったようにも思えますが、実用的に考えると実はそんなに検索効率は変わりません。

１番の理由は、KMP 法ではパターンの先頭の文字と２文字目の文字で不一致した場合、完全に力まかせ法と同様の処理になってしまう点ですね。文字列検索なんてだいたい先頭の文字と２文字目の文字で不一致しますからね…。

事前に “適切な位置” を求めておく分、KMP 法の方が力まかせ法よりも遅いケースもあり得そうです。

ですが、逆にパターンの先頭の文字と２文字目の文字で一致することが多い場合（例えばパターンの先頭文字列と似ている部分がテキストの中に多い場合など）は、力まかせ法に比べて効率の良い文字列検索アルゴリズムになると思います。ただ通常の英文でそういうテキストがあるかというとレアなケースのみだと思いますので、実用性としては低いアルゴリズムであると考えることができます。