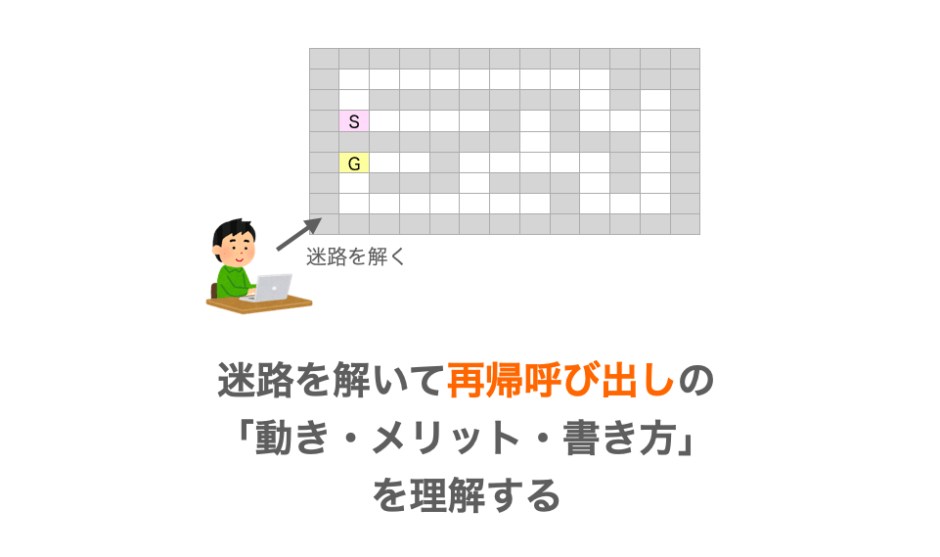
今回は「迷路を解く」というお題で「再帰呼び出し」について学んで行きたいと思います。
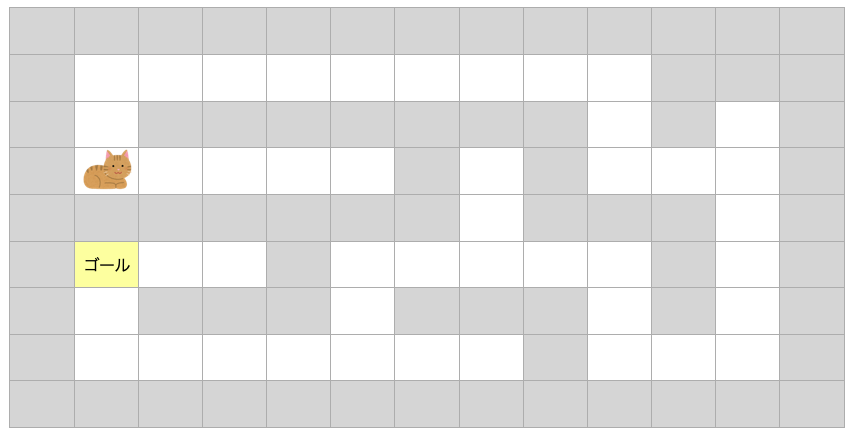
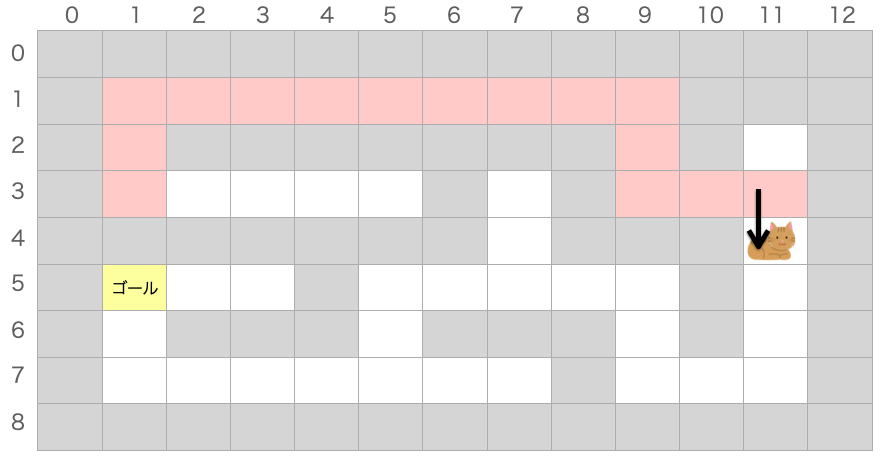
猫がいる位置がスタートで、この猫をゴールまで移動させることで迷路を解くプログラムを作成します。
ただし、迷路を解く際には下記の2つの条件を満たすことをルールとしたいと思います。
- 壁は通れない
- 一度通過したマスは通れない
主に上の図で示した迷路を用いて説明していますが、スタートからゴールまで道が続いていればどんな迷路でも解けるプログラムを考えていきます。
「迷路を解く」と聞くと難しそうに感じるかもしれませんが、実は「再帰呼び出し」を利用すれば簡単に書けます!

再帰呼び出し…
あれ苦手…

再帰呼び出し難しいよね
なので今回はとっつきやすい「迷路」を使って詳しく解説していくよ!

再帰呼び出しの便利さを知るためにも程よいお題だと思う

「迷路を解く」は再帰呼び出しについて学ぶにベストなお題だと思います。
では早速「迷路を解く」プログラムについて紹介し、続いてこのプログラムを用いて下記を解説していきたいと思います。
- なぜこのプログラムで迷路が解けるのか?
- 再帰呼び出しはどのように動作するのか?
- 再帰呼び出しで「難しい問題」が簡単に解ける理由は?
最後に、これらの解説を踏まえて「再帰関数の書き方のポイント」も紹介していきたいと思います。
Contents
迷路を解くプログラム
迷路を解くC言語プログラムは下記のようになります。
#include <stdio.h>
/* 迷路のサイズ */
#define MEIRO_WIDTH 13
#define MEIRO_HEIGHT 9
#define PATH 0 /* 通路 */
#define WALL 1 /* 壁 */
#define GOAL 2 /* ゴール */
#define PASSED 3 /* 通過したマス */
/* 迷路を表す配列(0:通路、1:壁) */
static int maze[MEIRO_HEIGHT][MEIRO_WIDTH] =
{
{1,1,1,1,1,1,1,1,1,1,1,1,1},
{1,0,0,0,0,0,0,0,0,0,1,1,1},
{1,0,1,1,1,1,1,1,1,0,1,0,1},
{1,0,0,0,0,0,1,0,1,0,0,0,1},
{1,1,1,1,1,1,1,0,1,1,1,0,1},
{1,0,0,0,1,0,0,0,0,0,1,0,1},
{1,0,1,1,1,0,1,1,1,0,1,0,1},
{1,0,0,0,0,0,0,0,1,0,0,0,1},
{1,1,1,1,1,1,1,1,1,1,1,1,1}
};
/* 関数のプロトタイプ宣言 */
void print(void);
void move(int, int);
/* 経路を表示する関数 */
void print(void) {
int i, j;
for (j = 0; j < MEIRO_HEIGHT; j++) {
for (i = 0; i < MEIRO_WIDTH; i++) {
/* 配列の値に応じて記号/文字を表示 */
if (maze[j][i] == PATH) {
printf(" ");
}
if (maze[j][i] == WALL) {
printf("#");
}
if (maze[j][i] == PASSED) {
printf("o");
}
if (maze[j][i] == GOAL) {
printf("G");
}
}
printf("\n");
}
printf("\n");
}
/* (i,j) マスから移動できる方向に1マス進む関数 */
void move(int i, int j) {
int ni, nj; /* 次の位置を格納する変数 */
/* 迷路外 or 壁のマスが指定された場合はエラー */
if (i < 0 || i >= MEIRO_WIDTH || j < 0 || j >= MEIRO_HEIGHT || maze[j][i] == WALL) {
return ;
}
/* このマスがゴールなら終了 */
if (maze[j][i] == GOAL) {
/* ここまでの経路を表示 */
print();
return ;
}
/* このマスを通過したことを覚えておく */
maze[j][i] = PASSED;
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
if (nj >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 下に1マス移動 */
ni = i;
nj = j + 1; /* 下に移動 */
if (nj < MEIRO_HEIGHT) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 左に1マス移動 */
ni = i - 1; /* 左に移動 */
nj = j;
if (ni >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 右に1マス移動 */
ni = i + 1; /* 右に移動 */
nj = j ;
if (ni < MEIRO_WIDTH) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 関数実行前後でmazeが変わらないようにmazeを元に戻しておく */
maze[j][i] = 0;
}
int main(void) {
/* ゴールの位置を設定 */
maze[5][1] = GOAL;
/* スタート位置を(1,3)として開始 */
move(1, 3);
return 0;
}
maze 配列は各マスの情報を表す2次元配列です。各数字によって下記を表しています(括弧内は define 名になります)。
0(PATH):通路1(WALL):壁2(GOAL):ゴール3(PASSED):既に通過した通路
配列初期化時も 0 や 1 ではなく define 名を使用する方が良いのですが、横に長くなってしまうのであえて 0 と 1 を使用しています。
この maze 配列を変更すれば、解く迷路を変更できます。上で示した maze 配列は最初にお見せした迷路になります。
実行すると下記のようにゴールまでのルートが表示されます(全て文字で表現しているので見にくいですが…)。
“o” が通過したマス、”#” が壁、”G” がゴールを表しています。
############# #ooooooooo### #o#######o# # #o # #ooo# ####### ###o# #G #ooooo#o# #o###o###o#o# #ooooo #ooo# #############
で、この迷路を解いているのが move 関数になります。

「迷路を解く」って聞くと難しそうに感じたけど、
move 関数を実際見てみたら思ったよりも簡単だった!
これなら僕にもプログラミングできそう
その感覚大事だよ!
再帰呼び出しを使えば難しい問題も簡単に解けちゃうんだ


そこは順を追って解説していくよ!
まずは「なぜこのプログラムで迷路が解けるのか?」について解説していくよ

実際に move 関数を見て「思ったよりも簡単だった」と思った人も多いのではないでしょうか?
「なぜこんな簡単な関数で迷路が解けるのか?」について次は解説していきたいと思います。
迷路を解く考え方
「迷路を解くとは具体的にどのような処理なのか」を考えることが、「なぜこんな簡単な関数で迷路が解けるのか?」の答えになります。
まずは、あなたが下の図の迷路を解く時にどのように考えて解くかをちょっと考えてみましょう。

おそらく迷路を解く際は頭の中で下記のような操作を繰り返すのではないかと思います。
- 移動できる方向に1マス進む
- 1マス戻る
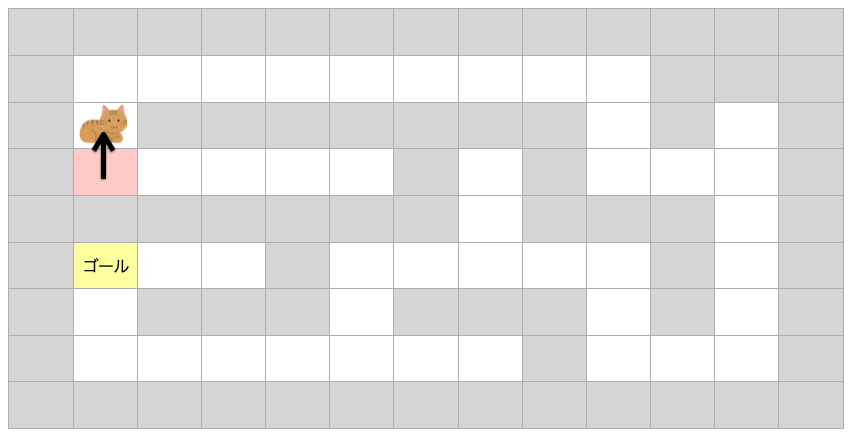
例えば最初に紹介した迷路であれば、猫のいる位置から、まずは移動できる方向に「1マス進む」を行いますよね?
移動できる方向が上と右の2つありますが、今回は上方向を選んでみましょう。上方向がダメなら後から右方向への移動を試してみればいいだけです(赤いマスは既に通過したマスを表しています)。
次は移動したマスからさらに移動できる方向に「1マス進む」を行います。移動できる方向は上方向だけ(下は一度通過したマスなのでダメ)なので迷わず上に「1マス進む」を行えば良いですね!
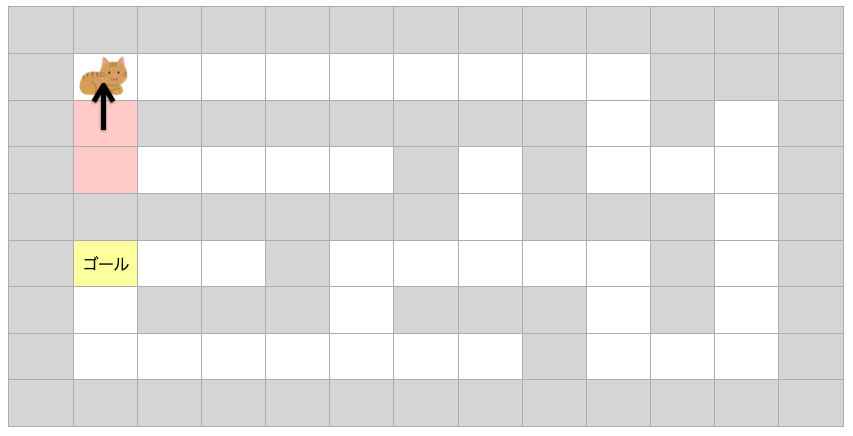
で、この「移動できる方向に1マス進む」を繰り返します。しばらくは移動できる方向が1方向だけなので説明は省略します。
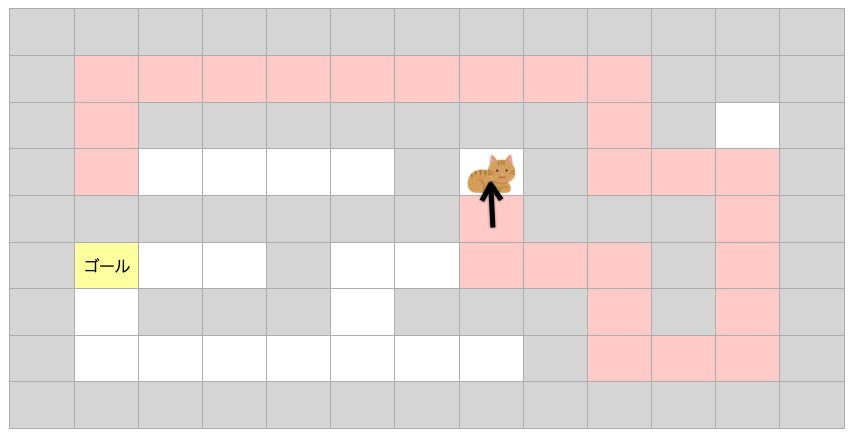
いずれは移動できる方向が複数存在するマスにたどり着きます。
例えば下のマスだと猫が進むと上方向と左方向の2方向(右は一度通過したマスなのでダメ)に移動可能です。
ここでは上方向移動してみましょう!
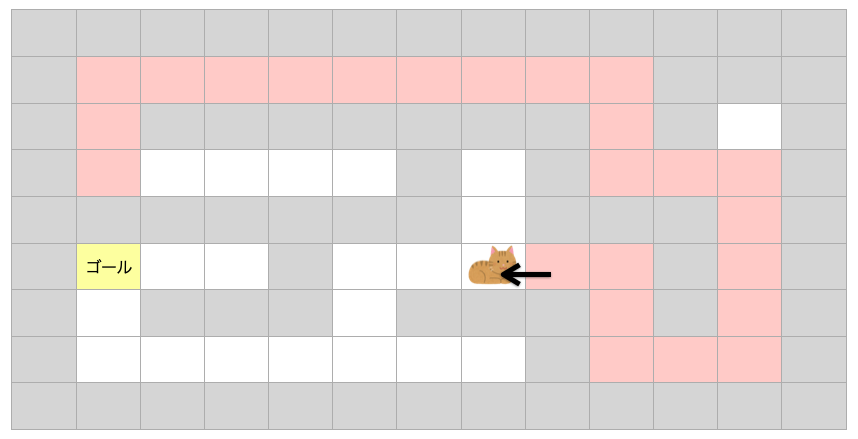
すると、「移動できる方向に1マス進む」を繰り返し行うと、いずれ行き止まりのマス(どの方向にも移動できないマス)に辿り着きます。
この場合、このルートは正解ではなかったと言うことです。
なので、1マス戻ります。
そして1マス戻った先で、移動可能なマスがあるかを確認します。
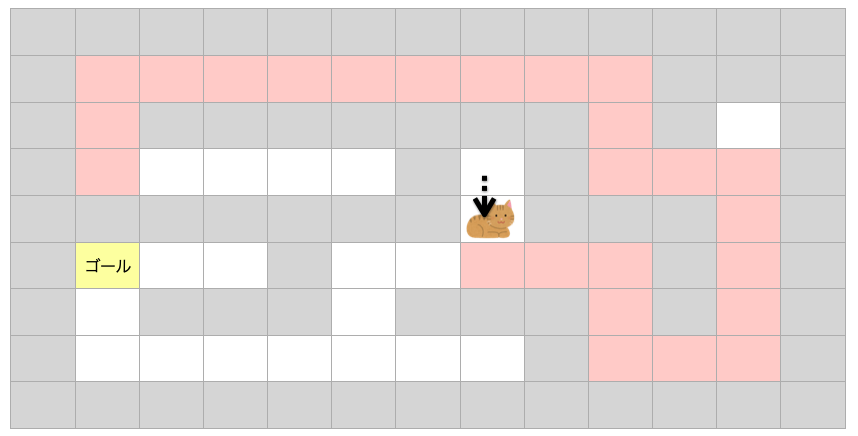
ただし、このマスに関しては、上方向はすでに試して正解では無いルートであることは分かっていますし、下方向は一度通過したマスなので、移動可能なマスは無いと判断できます。
なのでさらに1マス戻ります。
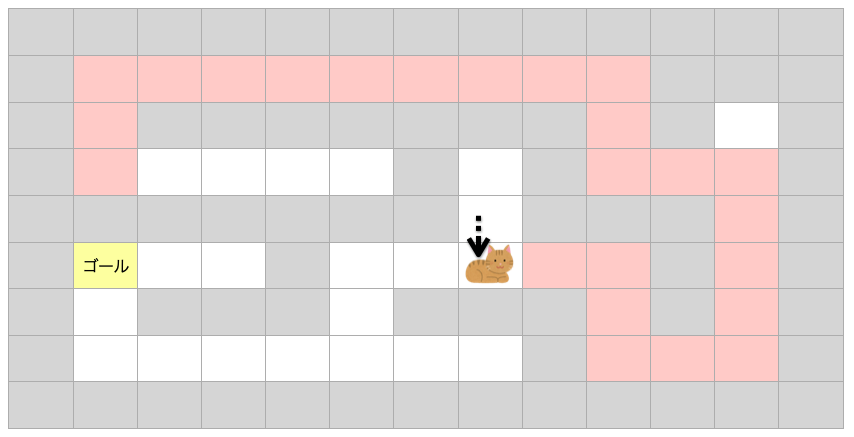
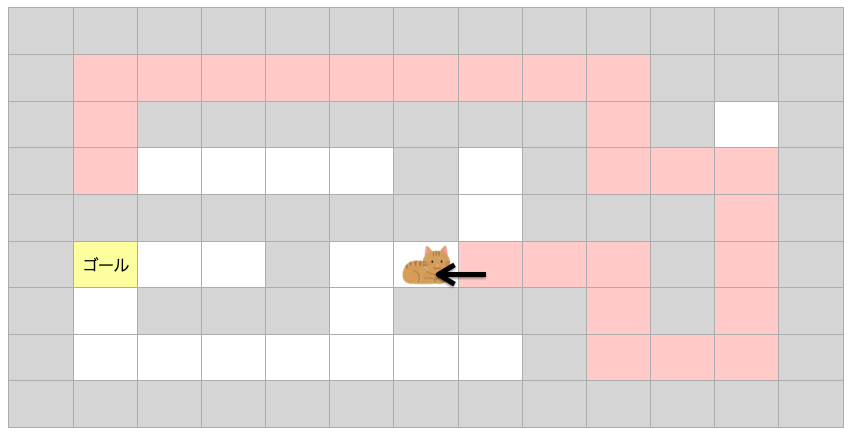
このマスは左方向をまだ試してないので、移動できると判断し、また「移動できる方向に1マス進む」を繰り返していきます。
後は同じことを繰り返してやれば、いずれゴールに辿り着きます。
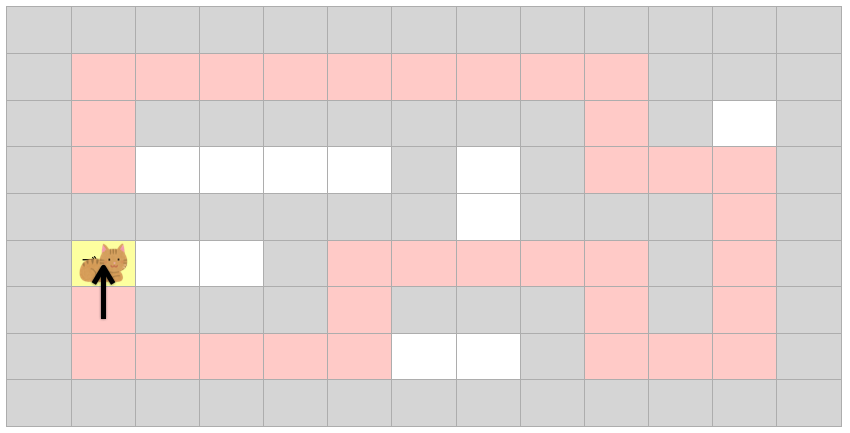
おそらく、あなたも迷路を解く場合は上記のようなことを頭の中で考えて迷路を解くのではないかと思います。
何が言いたいかというと、「迷路を解く」は下記の2つを繰り返すことで実現可能だということです。
- 移動できる方向に1マス進む
- 1マス戻る
そして、これらを行っているのが move 関数になります。move 関数を move 関数の中で再帰呼び出しすることで、move 関数がどんどん繰り返し実行されますので、「移動できる方向に1マス進む」「1マス戻る」が繰り返し行われることになります。

待った!
move 関数で1マス進むのはソースコード読めばなんとなく分かるよ?
でも1マス戻るような処理を行っているようには見えない…
オーケー!
次は move 関数の動き、特に再帰呼び出しの動きについて説明していくよ
この説明で、なぜ move 関数で1マス戻るのかも理解できるはず!

次は実際に move 関数の、特に再帰呼び出し部分がどのように動作して迷路を解くのかについて解説していきます。
スポンサーリンク
再帰呼び出しの動き
では move 関数の、特に再帰呼び出し部分がどのように動作するのかについて解説していきます。
ここからは迷路の各マスの位置を座標で考えていきたいと思います。
原点は一番左上のマスとします。つまり、一番左上のマスの座標が (0, 0) になります。縦方向における下、横方向における右をそれぞれ正方向とすれば、下記のように各マスの座標を表すことができます。
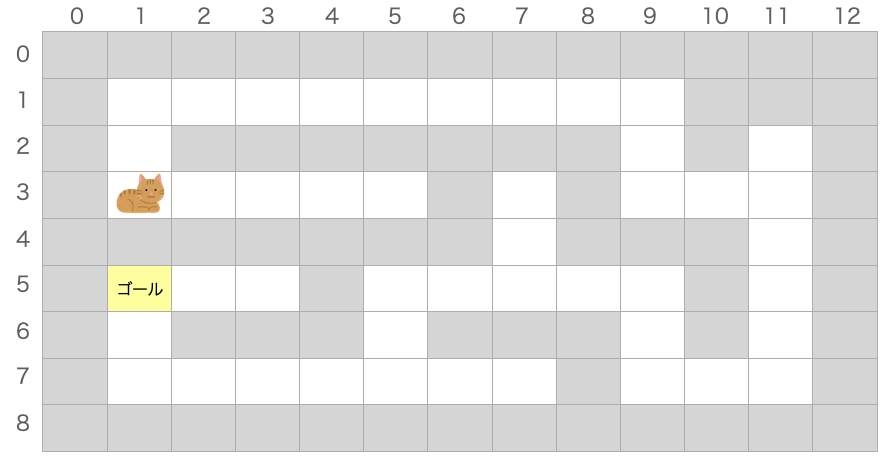
例えば猫がいる座標は (1, 3) になります。なので、猫が上方向に1マス進めば猫がいるマスの座標は (1, 2) に、猫が右方向に1マス進めば猫がいるマスの座標は (2, 3) になります。
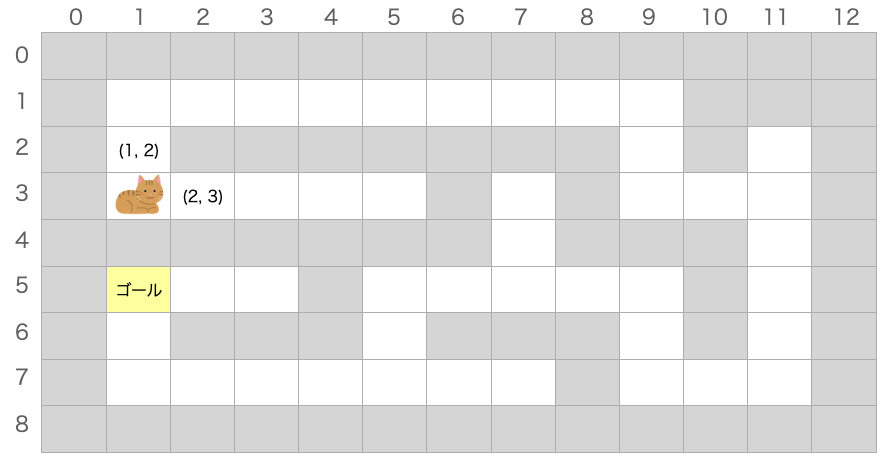
こんな感じで座標の一方(横 or 縦)に +1 or -1 すれば、猫が1マス進むことになります。
ここまでの説明を意識して move 関数を読んでみましょう。
move関数の実行 = 移動できる方向に1マス進む
まず move 関数の引数は現在地のマスの座標 (i, j) を表す値としています。
さらに move 関数実行時に、現在地に対して主に下記の2つのことを行っています。
- 通過したマスの記録
- 1マス進んだ上で
move関数の再帰呼び出し
通過したマスの記録
この迷路では下記の場合はそのマスに進めないという条件があります。
- 一度通過したマスは通れない
なので、一度通過したマスを既に通過したかどうかを記録しておき、1マス進む処理を行う際に、その進もうとしているマスが既に通過しているかどうかを確認する必要があります。
そのため、下記で現在のマスの位置に PASSED を格納することで、後からそのマスを通過したかどうかを判断しています。
/* このマスを通過したことを覚えておく */
maze[j][i] = PASSED;1マス進んだ上で move 関数の再帰呼び出し
また move 関数の引数は現在地のマスの座標 (i, j) を表していますので、この j に -1 すれば、現在地のマスから上方向に1マス進むことになります。下方向に1マス進めるのであれば j に +1 すれば良いです。
また i に -1 すれば左方向に、+1 すれば右方向に1マス進むことになります。
ですので、move 関数の下記部分では「移動できる方向に現在地から1マス進めた上で move 関数を再帰呼び出し」していることになります。
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
if (nj >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 下に1マス移動 */
ni = i;
nj = j + 1; /* 下に移動 */
if (nj < MEIRO_HEIGHT) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 左に1マス移動 */
ni = i - 1; /* 左に移動 */
nj = j;
if (ni >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 右に1マス移動 */
ni = i + 1; /* 右に移動 */
nj = j ;
if (ni < MEIRO_WIDTH) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}4方向それぞれに対して移動可能かどうかを if 文で判断し、移動できる場合だけ move 関数の再帰呼び出しを行っています。
特に下記部分は一度通過したマスであればそのマスに移動しないようにするための if 文になります。
if (maze[nj][ni] != PASSED) {ではこの move 関数の再帰呼び出しにより、どのようにプログラムが動作するのかを、スタート地点の座標 (1, 3) のマスに対してmove 関数を実行した時の例で確認していきたいと思います。
まず (1, 3) マスの場合、移動可能なのは上方向と右方向になります。
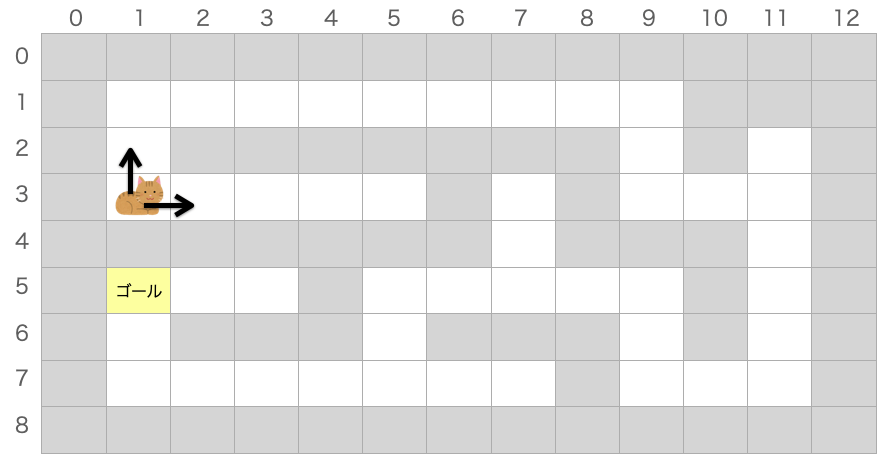
プログラムは基本的にソースコードの上側から先に実行されるので、まずは下記で move 関数が実行されることになります。
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
if (nj >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}このとき、j が -1 された状態で move 関数が実行されることになります。
つまり、「上方向に1マス進んだ上で move 関数が実行される」ことになります。
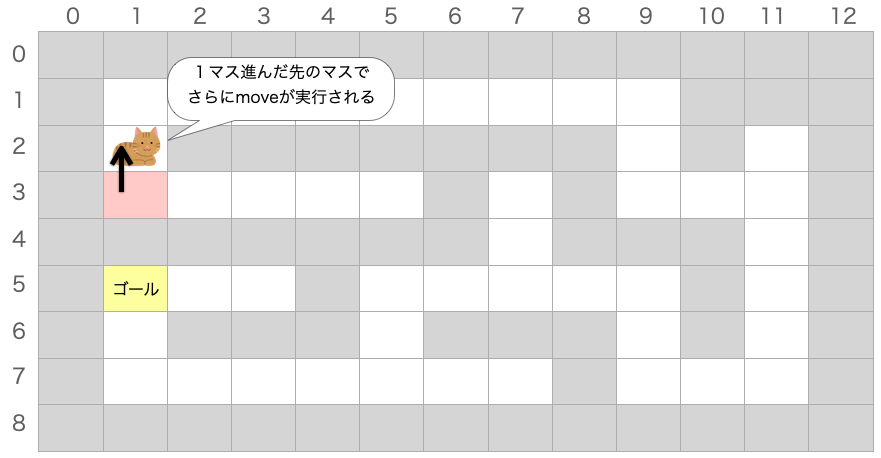
1マス進んだ先の座標は(1, 2)なので、i=1、j=2 として move 関数が実行されることになります。
座標(1, 2)のマスは上方向のみに移動可能です(下方向は既に通過したマスなので移動できない)。
なのでこの時は、先ほどと同様に下記の部分でさらに上方向に移動した上(j - 1 とした上)で、再び move 関数の再帰呼び出しが行われます。
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
if (nj >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}つまり、先ほどと同様に「上方向に1マス進んだ上で move 関数が実行される」ことになります。
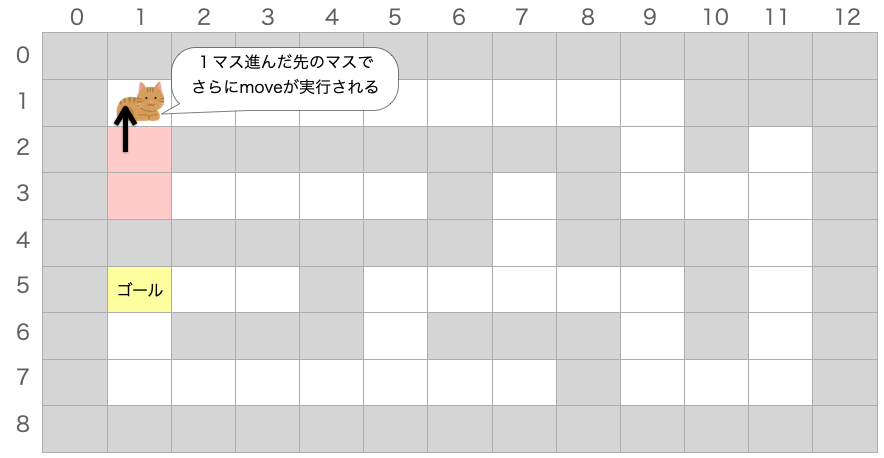
1マス進んだ先の座標は(1, 1)なので、今度は i=1、j=1 として move 関数が実行されることになります。
マス (1, 1) は移動できるのが右だけ(下は既に通過したマスなので移動できない)なので、下記で右の方向に1マス進んだ上で(i + 1 とした上で)、 move 関数が実行されることになります。
/* 右に1マス移動 */
ni = i + 1; /* 右に移動 */
nj = j ;
if (ni < MEIRO_WIDTH) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}つまり、「右方向に1マス進んだ上で move 関数が実行される」ことになります。

こんな感じで move 関数を再帰呼び出ししてやるだけで、「移動できる方向に1マス進む」を行った上で、さらに「移動できる方向に1マス進む」を繰り返し行うことができます。
ただし、これを繰り返していれば行き止まりマスに到着してしまうこともあります。
この場合は1マス戻り、他の方向に移動することを考える必要があります。
move関数の終了 = 1マス戻る
実はこの「1マス戻る」は move 関数の終了により実現することができます。
これついて、座標 (11, 3) のマスから1マス進むことを考えてみましょう!
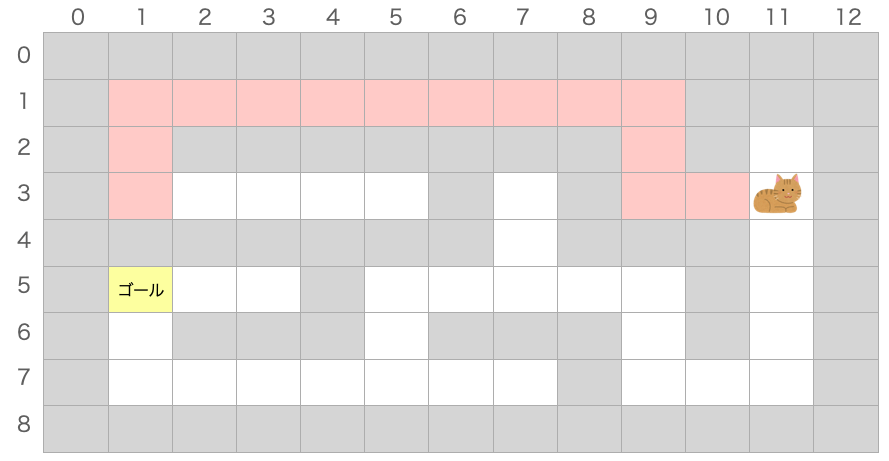
つまりこれは、move 関数の引数として i=11、j=3 が与えられたときの動きを考えることになります。
この時、上方向に移動できるので、下記で上方向に1マス進んだ上で(j - 1 した上で)、 move 関数が実行されます。
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
if (nj >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}なので引数 i=11、j=2 として move 関数が実行されることになります。つまり (11, 2) のマスから move 関数を実行することになります。
ただし、このマス (11, 2) からはもう移動できるマスがありません。上左右は壁ですし、下はすでに通過したマスです。
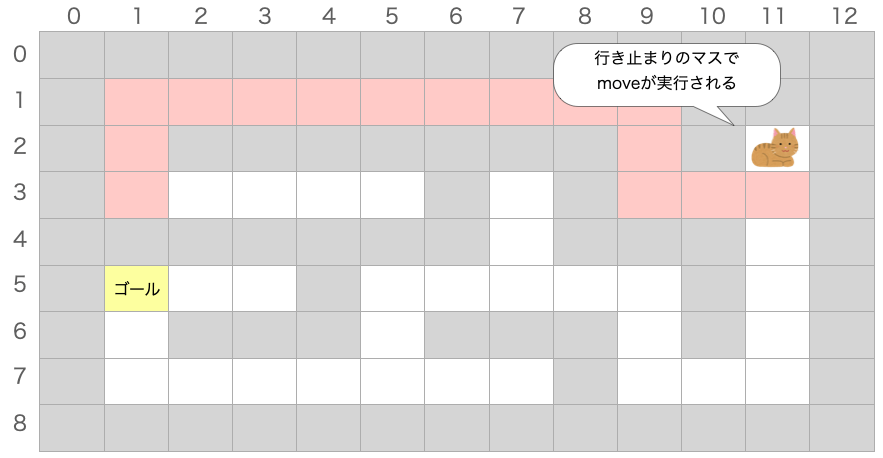
そのため、move 関数の if 文は全て成立しません。ですので 、move の再帰呼び出しは行われず、すぐに関数を終了することになります。
では関数が終了するとどうなるでしょう?
結論を先に言うと「1マス戻る」ことになります。
まず前提として呼び出した関数は終了すると、呼び出し元に戻ります。
例えば下記のソースコードの場合、calc 関数から add 関数を呼び出すと、add 関数が実行され、add 関数が終了すると calc 関数に戻り、 add 関数を呼び出した直後の処理から再開されます。
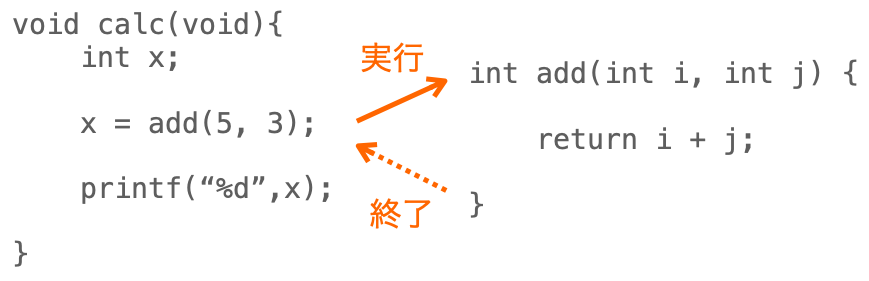
これは再帰呼び出しの場合も同様です。先ほどの例で言えば、下記のような動きで関数の呼び出しが行われることになります。
- 引数を
i=11、j=3として呼び出されたmove関数の中で、引数をi=11、j=2としてmove関数を呼び出す - 引数を
i=11、j=2として呼び出されたmove関数の処理が実行され、やがて処理が終了する - 呼び出し元の関数(引数を
i=11、j=3として実行されたmove関数)に戻る
引数 i と j はマスの座標を表しますので、1. で1マス進み、3. で1マス戻ることになります。
つまり、1マス進めた上で再帰呼び出しを実行した場合、その再帰呼び出しで実行された関数が終了すれば1マス戻ることになります。
ですので、先ほどの例でいえば、引数を i=11、j=2 として実行された move 関数が終了すれば、(11, 2) のマスから元のマス (11, 3) に1マス戻ることになります。
具体的には引数 i=11、j=3 として実行された move 関数の部分に戻ります。
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
if (nj >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
/* ここから処理が再開される */
}
}
}さらに、引数 i=11、j=3 として実行された move 関数は一部の処理(上方向への移動)しか行っていませんので、下記の残りの処理が続けて実行されることになります。
/* 下に1マス移動 */
ni = i;
nj = j + 1; /* 下に移動 */
if (nj < MEIRO_HEIGHT) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 左に1マス移動 */
ni = i - 1; /* 左に移動 */
nj = j;
if (ni >= 0) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}
/* 右に1マス移動 */
ni = i + 1; /* 右に移動 */
nj = j ;
if (ni < MEIRO_WIDTH) {
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
}つまり、下・左・右方向に移動できる場合は move 関数を再帰呼び出しする処理が実行されます。
このマスの場合は下方向に移動可能なので、下方向に移動した上で move 関数が実行され、どんどん「移動できる方向に1マス進む」が繰り返し行われていきます。
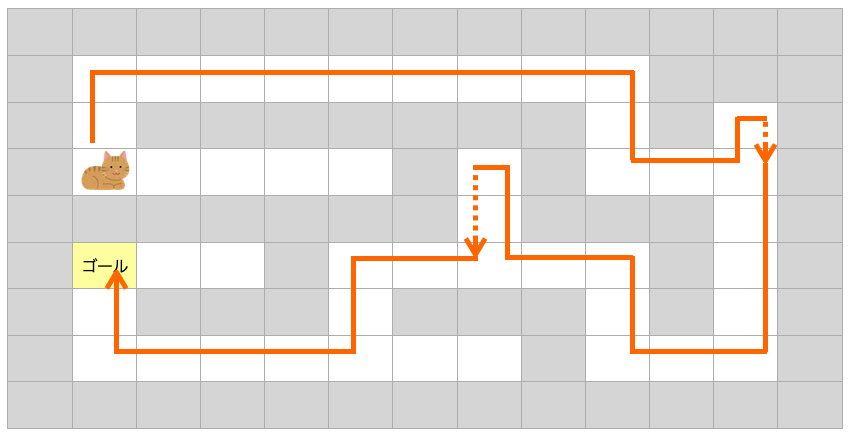
ポイントはすでに試した上方向への処理はすでに終了しているので、もうその方向には移動しない点です。
もう試したルートは答えが分かっている(今回の場合は行き止まりであることが分かっている)のでもう移動する必要はないですよね?
こんな感じで、「1マス戻る」は単純に move 関数を終了するだけで実現することができます。
もし1マス戻った先のマスも移動可能なマスがない場合は連続して move 関数が終了し、「1マス戻る」が連続して行われることになります。
今回は迷路の例なので「1マス戻る」という表現になりますが、一般的には「一手進めた上で再帰呼び出しを行う」と、その再帰呼び出しした関数が終了すると「一手戻る」ことになります。
この「一手戻る」を簡単に実現できるのも再帰呼び出しのメリットだと思います。
スポンサーリンク
ゴール到着時の処理
このように「移動できる方向に1マス進む」の繰り返しと「1マス戻る」の繰り返しにより、(通路がちゃんと通じていれば)いずれはゴールのマスに到達し、ゴールのマスに対して move 関数が実行されることになります。
今回紹介した move 関数の場合は、移動できるマスが複数ある場合は上・下・左・右の順で移動するように関数を作成しているため、下図のようなルートでゴールまでたどり着きます(「1マス戻る」は点線で表しています)。
ゴールまで到達した場合、move 関数では下記の if 文が成立し、print 関数が実行されてここまでの経路を表示したのち、return により関数が終了します。
/* このマスがゴールなら終了 */
if (maze[j][i] == GOAL) {
/* ここまでの経路を表示 */
print();
return ;
}ポイントは、上記では move 関数の再帰呼び出しを行っていない点です。
再帰呼び出しを行わないので、print 関数実行後に直ちに関数が終了します。関数が終了すると「1マス戻る」と同じ動きになります。
「1マス戻る」で説明したように、戻った先のマスにまだ移動できる方向があればその方向に進みますし、移動できる方向がなければ「1マス戻る」を繰り返すことになります。
つまり、今度は他のルートを自動的に探し出すというわけです。
今回の例ではゴール到着後も下図のようにマスを移動することになります。
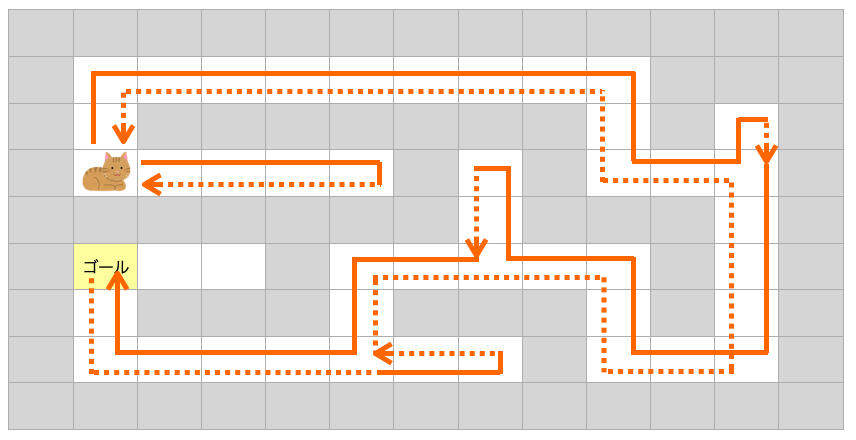
最初にスタート地点から上方向に移動したので、先にその方向に対して進んで行きましたが、その方向に進み切ったら、もう一つの移動できる方向である右方向にも移動していく事になります。
最終的には移動可能&ゴールに到達できる可能性があるルートを全て試す事になります。
今回はゴールに辿り着けるルートが1つだけですが、ゴールに辿り着けるルートが複数ある場合はその全てのルートを表示するようなこともできます。
こんな感じで考えられる全パターンを試す際にも再帰呼び出しは非常に便利です。

なるほど
move 関数の動きはだいたい分かったよ!
move は1マス進むだけの関数に見えて、再帰呼び出しによって「移動できる方向に1マス進む」を繰り返す&関数終了したら「1マス戻る」を行うことができるようになってるんだね!


move 関数のあれだけの処理で迷路が解けてしまうのはやっぱり不思議だなぁ…オーケー
次は「なぜ再帰呼び出しにより難しい問題が簡単に解けるのか?」について解説していくよ

再帰呼び出しのメリット
再帰呼び出しの最大のメリットは「難しい問題」を「簡単な問題」に置き換えて解くことができるところです。
再帰呼び出しにより難しい問題を簡単な問題で解ける
今回の迷路の場合は「難しい問題」と「簡単な問題」は下記のようになります。
- 難しい問題:迷路を解く
- 簡単な問題:移動できる方向に1マス進む(1マス戻る)
「迷路を解く」と聞いた時、プログラミングするの難しそう…と思いませんでしたか?
しかし、どうでしょう?出来上がった move 関数を見てみると 「”想像したより” も簡単だった」と思いませんか?
ここが、再帰呼び出しの一番のメリットです!
実際に move 関数で行っているのは、ゴールについた時の処理を除けば「移動できる方向に1マス進む」+「再帰呼び出し」だけですよね!
ここからも上記のように、”再帰呼び出しを行うことで「難しい問題」を「簡単な問題」に置き換えて解くことができる” ことを実感していただけるのではないかと思います。
では「なぜ再帰呼び出しを行えば難しい問題を簡単な問題で解けるのか?」について解説しておきたいと思います。
ここでまず考えたいのが「迷路を解く」における「移動できる方向に1マス進む」を行うことの意味です。
2つあると思います。
まず1つ目は「答えに一段階近づける」ことができることです。
“答え” とは、今回は「迷路を解く」なのでゴール到達ですね。また、行き止まり到達もそうです。これも、そのルートがゴールに到達できないという一つの答えですよね?
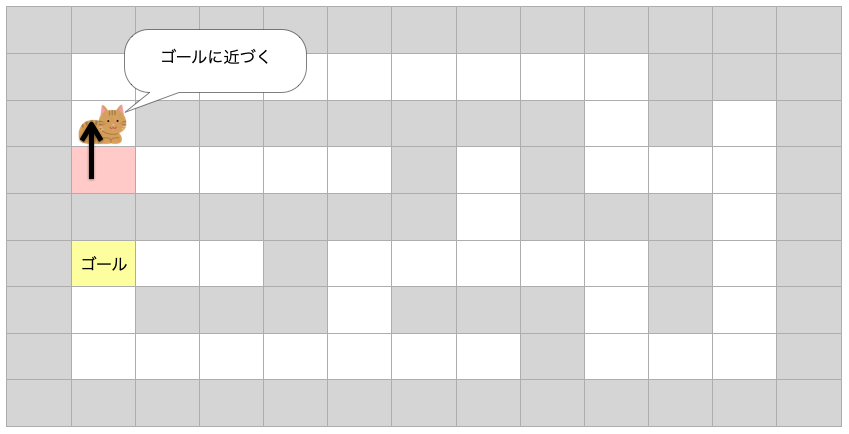
2つ目は「問題を一段階簡単にする」ことができることです。
この迷路の場合、下記のルールがあります。
- 一度通過したマスは通れない
つまり「1マス進む」ということは通過できるマス数が1つ減るということになります。
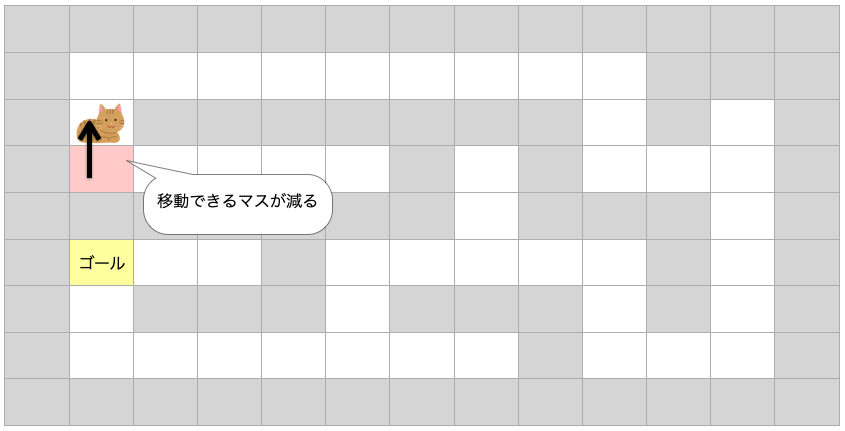
通過できるマスが減れば迷路は一段階簡単になりまよね?
この2つの側面があると考えれば、「1マス進んだ上で move 関数を再帰呼び出しする」とは、「一段階答えに近づけ、問題を一段階簡単にした上で move 関数を再帰呼び出しする」ことと考えられます。
再帰呼び出しされた move 関数の中では、さらに move 関数の再帰呼び出しが行われるので、move 関数が繰り返し実行されることになります。
また move 関数を実行することで「答えに一段階近づく」「問題が一段階簡単にする」ことになりますので、どんどん答えに近づき、さらに問題が簡単になっていくことになります。
当然いずれは答えに辿り着きます(ゴール or 行き止まり)。
何が言いたいかと言うと「答えに一段階近づけ、問題を一段階簡単にした上で再帰呼び出しをするように関数を作成する」だけで、勝手に難しい問題も解けてしまうということです。
つまり、難しい問題であっても、その答えを導くのに実質的にプログラミングする必要があるのは、「答えに一段階近づける」「問題を一段階簡単にした上で再帰呼び出しする」ことだけなんです!
なので、再帰呼び出しを利用すれば、難しい関数も簡単な関数の再帰呼び出しで案外プログラミングできてしまったりしますよ!
スポンサーリンク
再帰関数の作り方のポイント
最後に、ここまでの解説を踏まえて再帰関数の作り方のポイントを整理しておきたいと思います。
再帰関数とは「再帰呼び出しを行う関数」のことです。
特に「難しい問題」を解きたい場合、この再帰関数で基本的に記述すべきことは下記の3つです。
- 答えに一段階近づける処理
- 問題を一段階簡単にした上での再帰呼び出し
- 答えが明らかになった時に再帰呼び出しを行わない制御
答えに一段階近づける処理
再帰関数に記述すべきことの1つ目は「答えに一段階近づける処理」です。
迷路を解く場合は「移動できる方向に1マス進む」処理ですね。
move 関数では下記がこの「答えに一段階近づける処理」になります。
/* 上に1マス移動 */
ni = i;
nj = j - 1; /* 上に移動 */
/* 〜略〜 */
/* 下に1マス移動 */
ni = i;
nj = j + 1; /* 下に移動 */
/* 〜略〜 */
/* 左に1マス移動 */
ni = i - 1; /* 左に移動 */
nj = j;
/* 〜略〜 */
/* 右に1マス移動 */
ni = i + 1; /* 右に移動 */
nj = j; ゴールに到達するのが答えなので、1マス分ゴールに近づける上記の処理が、この「答えに一段階近づける処理」になります。
もちろんゴールではなく行き止まりに近くこともありますが、行き止まりも「ゴールへのルートではないという答え」と考えると、上記の処理は「答えに一段階近づける処理」と考えることができます。
問題を一段階簡単にした上での再帰呼び出し
再帰関数に記述すべきことの2つ目は「問題を一段階簡単にした上での再帰呼び出し」です。
move 関数の場合は「問題を一段階簡単にする」処理は下記になります。通過したマスを記録する処理ですね。
/* このマスを通過したことを覚えておく */
maze[j][i] = PASSED;これにより既に通過したマスが増えるので、今後移動できるマスが減ることになります。
なので問題が簡単になります。
さらに、上記を行った上で、再帰呼び出しを行っています。
/* 次のマスからゴールまで移動させる */
move(ni, nj);これにより、問題が簡単になった状態で move 関数が実行されることになります。
「一段階簡単にする」と聞いてもイメージが湧かない人もいるかもしれませんが、よくあるパターンが「範囲を一段階狭くする」ですね。
スポンサーリンク
答えが明らかになった時に再帰呼び出しを行わない制御
最後に記述すべきことは「答えが明らかになった時に再帰呼び出しを行わない制御」です。
下記の2つを繰り返し行えば、いずれは答えが明らかになります。
- 答えに一段階近づける処理
- 問題を一段階簡単にした上での再帰呼び出し
答えが明らかになった時には再帰呼び出しを行わないように制御します。
再帰呼び出しを常に行うような再帰関数を作ってしまうと、無限に再帰呼び出しが行われることになるので注意しましょう。
実際には無限に再帰呼び出しが行われるのではなく、途中でスタックオーバーフローで異常終了することになります
迷路の場合は、答えは「ゴールへの到達」と「行き止まりへの到達」なので、下記で「ゴールへの到達」が明らかになった時に再帰呼び出しを行わないようにしています。
/* このマスがゴールなら終了 */
if (maze[j][i] == GOAL) {
/* ここまでの経路を表示 */
print();
return ;
}また「移動できる方向がない」が明らかになった時に再帰呼び出しを行わないように if 文で制御しています。
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
/* 〜略〜 */
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
/* 〜略〜 */
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}
/* 〜略〜 */
if (maze[nj][ni] != WALL) {
if (maze[nj][ni] != PASSED) {
/* 次のマスからゴールまで移動させる */
move(ni, nj);
}
}if 文全てが成立しない場合は行き止まりのマスなので、再帰呼び出しが行われないようにしています。
簡単な例でおさらい
最後に簡単な例で再帰関数の作り方のおさらいをしておきましょう。
意識すべきは下記の3つを記述することです。
- 答えに一段階近づける処理
- 問題を一段階簡単にした上での再帰呼び出し
- 答えが明らかになった時に再帰呼び出しを行わない制御
例としては「m 〜 n までの整数の足し算」を取り扱いと思います。
下記が「m 〜 n までの整数の足し算」を再帰呼び出しにより計算する関数になります。
int sum(int m, int n) {
if (m == n) {
return n;
}
return sum(m, n- 1) + n;
}答えに一段階近づける処理
m 〜 n までの整数の足し算の計算は、下記のように整数を1つずつ足し合わせることで実現することができます。
m + (m+1) + (m+2) + ・・・ + (n-2) + (n-1) + n
答えに一段階近づけるためには値を1つだけ足し合わせてやれば良いですよね?
今回は足し合わせる範囲の一番最後の整数(n)を足し合わせるようにすることで、「答えに一段階近づける処理」を行わせています。
具体的には下記の黄色背景部分になります。
return sum(m, n- 1) + n;迷路の例では、この「答えに一段階近づける処理」は再帰呼び出しを行う前に実行していました。
一方で、この例では再帰呼び出し実行の後に「答えに一段階近づける処理」が行われることになります。
このように「答えに一段階近づける処理」は再帰呼び出しの前後のどちらで行うべきかをしっかり考慮して再帰関数を作成する必要があります。
問題を一段階簡単にした上での再帰呼び出し
これは下記の黄色背景部分により行っています。
return sum(m, n- 1) + n;n - 1 を行った上で再帰呼び出ししていますので、一段階計算を行う範囲が狭まっています。
なので問題が1段階簡単になっています。
一段階計算を行う範囲を狭めるために m + 1 を行った上で再帰呼び出しする考え方もあります。
この場合、再帰呼び出しにより実行される sum 関数では m + 1 から n までの足し算が行われることになります。
ですが、今回は「答えに一段階近づける処理」で n の足し合わせを行うようにしているので、辻褄が合わなくなって計算結果がおかしくなってしまいます。
なので、「答えに一段階近づける処理」で n の足し合わせを行うようにする場合は n - 1 を行った上で再帰呼び出しする必要があります。
こんな感じで「答えに一段階近づける処理」と「問題を一段階簡単にした上での再帰呼び出し」は辻褄が合うようにセットで考える必要があります。
答えが明らかになった時に再帰呼び出しを行わない制御
n - 1 を行った上で再帰呼び出しが行われるので、再帰呼び出しするたびに計算する範囲が狭まっていくことになります。
つまり sum 関数に指定される引数 m と n の差がどんどん狭まっていきます。
いずれは m と n の値が同じになります。
この時は計算するまでもなく、 「m 〜 n までの整数の足し算」の結果は n になります(m も同じ値なので n でも良い)。
なので、m と n の値が同じになった時は「答えが明らかになった」と判断し、下記部分で再帰呼び出しを行わないように制御しています。
if (m == n) {
return n;
}まとめ
このページでは「迷路を解く」というお題で、再帰呼び出しの下記について解説しました。
- 再帰呼び出しの動き
- 再帰呼び出しにより「難しい問題」が「簡単な問題」により解ける理由
- 再帰関数の作り方のポイント
「再帰呼び出し」ははっきり言って難しいと思います。私も苦手でした…。
ですが、「再帰呼び出し」は「難しい問題」を「簡単な問題」で解けるという大きなメリットがあります。
使いこなせると難しい問題も簡単な関数を作成して解けるようになるのでプログラミングも楽しくなると思います。
是非このページで再帰呼び出しの動きやメリットを実感し、再帰関数の書き方を理解していただければと思います。
再帰呼び出しに慣れるには、やはり再帰呼び出しを行うプログラムを作ってみるのが一番良いと思います。
下記のようなページで再帰呼び出しにより問題を解く例(ソートしたり正解パターンを見つけたり)をいろいろ紹介していますので、再帰呼び出しをもっと使ってみたいという方は、是非これらのページも読んでみてください!
 C言語でハノイの塔の解法プログラムを実装!
C言語でハノイの塔の解法プログラムを実装!
 【C言語】数独(ナンプレ)をプログラミングで解く【バックトラック法】
【C言語】数独(ナンプレ)をプログラミングで解く【バックトラック法】
 【C言語】エイトクイーン問題(Nクイーン問題)のバックラック法での解き方
【C言語】エイトクイーン問題(Nクイーン問題)のバックラック法での解き方
 マージソートを図を使って分かりやすく解説(C言語サンプルプログラム付き)
マージソートを図を使って分かりやすく解説(C言語サンプルプログラム付き)
 クイックソートを図を使って分かりやすく解説(C言語サンプルプログラム付き)
クイックソートを図を使って分かりやすく解説(C言語サンプルプログラム付き)
オススメの参考書(PR)
C言語学習中だけど分からないことが多くて挫折しそう...という方には、下記の「スッキリわかるC言語入門」がオススメです!
まず学習を進める上で、参考書は2冊持っておくことをオススメします。この理由は下記の2つです。
- 参考書によって、解説の仕方は異なる
- 読み手によって、理解しやすい解説の仕方は異なる
ある人の説明聞いても理解できなかったけど、他の人からちょっと違った観点での説明を聞いて「あー、そういうことね!」って簡単に理解できた経験をお持ちの方も多いのではないでしょうか?
それと同じで、1冊の参考書を読んで理解できない事も、他の参考書とは異なる内容の解説を読むことで理解できる可能性があります。
なので、参考書は2冊持っておいた方が学習時に挫折しにくいというのが私の考えです。
特に上記の「スッキリわかるC言語入門」は、他の参考書とは違った切り口での解説が豊富で、他の参考書で理解できなかった内容に対して違った観点での解説を読むことができ、オススメです。題名の通り「なぜそうなるのか?」がスッキリ理解できるような解説内容にもなっており、C言語入門書としてもかなり分かりやすい参考書だと思います。
もちろんネット等でも色んな観点からの解説を読むことが出来ますので、分からない点は別の人・別の参考書の解説を読んで解決していきましょう!もちろん私のサイトも参考にしていただけると嬉しいです!
入門用のオススメ参考書は下記ページでも紹介していますので、こちらも是非参考にしていただければと思います。
https://daeudaeu.com/c_reference_book/