今回はC言語で小数点以下の値を2進数に変換する方法について解説していきたいと思います。
紹介するソースコードはC言語のものですが、考え方についてはどのプログラミング言語においても活用できると思います。

小数点以下か…
整数でも難しかったからかなり難しそう…
そんな印象がするよね?
でも整数を2進数に変換する原理を理解していれば小数点以下の変換についてもすんなり理解できると思うよ

整数の2進数変換について理解しておくと小数点以下の変換方法も理解しやすいです。
整数の2進数変換については下記ページで解説していますので、整数の2進数変換に自信が無い方は先に下記ページをご覧いただくことをオススメします!
 【C言語】10進数から2進数への変換(正の整数編)
【C言語】10進数から2進数への変換(正の整数編)
基本的にこのページの解説は「正数」の小数点以下の値を2進数変換する方法について解説しています。
「負数」の場合はその値の絶対値に対してこのページで解説する方法で2進数変換し、その結果に対して2の補数を計算すれば良いはずです
もしくは正負の情報を表示するだけでも良いと思います
Contents
整数の2進数変換(復習)
まずは整数の2進数変換についておさらいしておきましょう。しっかり理解できている人は次の小数点以下の2進数変換までスキップしていただければと思います。
ここはおさらいですので駆け足で説明していきます。詳細については下記ページの特に「10進数から2進数への変換」と「剰余算と除算を繰り返す方法」を参照いただければと思います。
 【C言語】10進数から2進数への変換(正の整数編)
【C言語】10進数から2進数への変換(正の整数編)
整数は2の冪乗の倍数の和で表すことができる
まず前提として、10進数の整数はどんな値でも「2の冪乗の倍数の和」で表すことができます。
\(10進数 =・・・+ a_{2} \times 2^{2} + a_{1} \times 2^{1} + a_{0} \times 2^{0} \)
各項の係数の組み合わせは複数ありますが、各項の係数を 0 もしくは 1 の値に限定した場合は各項の係数の組み合わせは必ず1パターンのみになります。
スポンサーリンク
各項の係数の値を並べたものが整数の2進数となる
そして、各項の係数を 0 もしくは 1 の値に限定した場合の各項の係数を冪数が大きい項のものから順に左から並べたものが整数を2進数変換した結果になります。

剰余算と割り算を繰り返すことで2進数変換できる
で、ここまでの考え方を活用すれば、10進数の整数は割り算結果が 0 になるまで下記を繰り返すことで2進数変換を行うことができます。
- 10進数の整数を
2で剰余算し、結果を2進数の第0桁の値とする - 10進数の整数を
2で割り算する - その割り算結果を
2で剰余算し、結果を2進数の第1桁の値とする - 割り算結果を
2で割り算する - その割り算結果を
2で剰余算し、結果を2進数の第2桁の値とする…
つまり、2の冪乗の和で表される値に対し、剰余算と除算を繰り返すことで整数を2進数変換することができます。

ここまでは良く理解してるつもりだよ
でも小数点以下になると難しそう…
それがそうでもないんだ
ここまでの話を理解してるなら簡単だよ

ここまで整数の2進数変換について説明してきましたが、小数点以下の値の2進数変換も同じ考え方で行うことができます!
小数点以下の2進数変換
では、ここからが本題の「小数点以下の10進数の値の2進数変換」の説明になります。
ここまで説明してきたように、整数の10進数の2進数変換と同様の考え方で変換することができます。
スポンサーリンク
小数点以下の値も2の冪乗の倍数の和で表すことができる
整数は全て2の冪乗の倍数の和で表すことができると言いました。
では、小数点以下の値はどうでしょう?
実は10進数の小数点以下の値も同様に2の冪乗の倍数の和で表すことができます。
ただし、小数点以下の値の2の冪乗の冪数はマイナスの値になります。
\(小数点以下の値 = a_{-1} \times 2^{-1} + a_{-2} \times 2^{-2} + a_{-3} \times 2^{-3}・・・\)
例えば、0.5 であれば下記のように、
\(0.5 = 1 \times 2^{-1}\)
0.5625 であれば下記のように、2の冪乗の和で表すことができます。
\(0.5625 = 1 \times 2^{-1} + 0 \times 2^{-2} + 0 \times 2^{-3}+ 1 \times 2^{-4}\)
整数同様に、単に2の冪乗と言うと、1つの値に対して複数の係数の組み合わせのパターンが存在します。
しかし、係数を 0 と 1 のみに限定すれば、その値を表す2の冪乗の和における係数の組み合わせは1つのパターンのみになります。

で、これを利用すれば整数の時とほぼ同じ感じで2進数に変換できるよ

各項の係数の値を並べたものが小数点以下の値の2進数となる
そして、これも整数同様に、各項の係数を 0 もしくは 1 の値に限定した場合の各項の係数を冪数が大きい項のものから左側から順に並べたものが整数を2進数変換した結果になります。

2 の -1 乗の項が2進数の小数点以下第 1 桁、2 の -2 乗の項が2進数の小数点以下第 2 桁に対応してる感じです。
例えば、0.5625 は下記のように2の冪乗の和で表されるので、
\(0.5625 = 1 \times 2^{-1} + 0 \times 2^{-2} + 0 \times 2^{-3}+ 1 \times 2^{-4}\)
各項の係数を冪数が大きいものから順に小数点以下の左側から並べたものが 0.5625 を2進数変換した結果となります。
0.5625 = 0.1001
有限の桁数では誤差が出る場合がある
ただし、2進数変換したときに桁数が無限に続くような値も存在します。例えば 0.3 は桁数が無限になります。
0.3 = 0.0100110011001・・・
一方で、コンピュータで扱う値は基本的に有限桁のもののみです。例えばC言語では「型」が存在し、型ごとに扱える桁数が決まっています。
ですので、0.3 のような桁数が無限になるような値は2進数にはそのまま変換できないことになります。無限に続く桁を途中で切り捨てて扱われます。この桁の切り捨てによって元々の値に対して誤差が発生することになります。
誤差が発生した場合、2進数変換した結果を10進数に変換したとしても元の値にはそのまま戻らないことには注意しましょう。
スポンサーリンク
小数点以下の2進数変換の手順
では、どのようにプログラミングすれば小数点以下の10進数の値を2進数に変換できるかについて説明していきたいと思います。
前述の通り、小数点以下の値は下記のような2の冪乗の倍数の和で表すことができます。
\(小数点以下の値 = a_{-1} \times 2^{-1} + a_{-2} \times 2^{-2} + a_{-3} \times 2^{-3}・・・\)
さらにこれも前述の通り、上式の「各項の係数を冪数が大きいものから順に小数点以下の左側から並べたもの」が、その値を2進数で表したものになります。

なので、各項の係数の値が 0 と 1 のどちらかを求めれば、2進数変換はもう出来たようなものです。
整数とは異なり、小数点以下の値の場合、2の冪乗の冪数はマイナスの値になります。
が、特に身構えることなく、整数の時と同様に考えれば良いです。
2 の掛け算で冪数を +1 する
まずは2進数に変換した時の小数点以下第 1 桁を求めることを考えてみましょう!
ここまで解説してきた通り、つまりは 2 の -1 乗の項の係数の値を求めます。
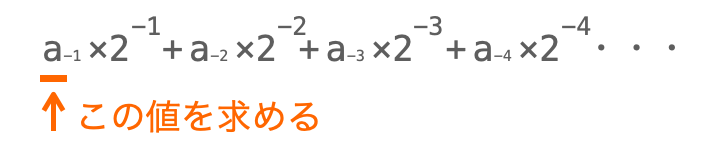
2の冪乗の値は 2 を掛けることで冪数が +1 されるという性質があります。
したがって、2進数変換したい小数点以下の値に対して 2 を掛ければ、2の冪乗の和で表された各項の冪数が全て +1 されることになります。

ここで、元々 2 の -1 乗の項だった項に注目すると、この項は 2 を掛けることで 2 の 0 乗の項になります。
つまり、小数点以下ではなく、整数部の値になります。
2 の 0 乗の項を剰余算で調べる
2 を掛けることで 2 の -1 乗の項が 2 の 0 乗の項になりました。
ここで整数の2進数変換を思い出してみましょう。整数の2進数変換では 2 の 0 乗の項の係数を 2 での剰余算で求めましたね?
これと同様に、小数点以下の値の2進数変換においても 2 の 0 乗の項の係数を調べるために、2 で剰余算してやれば良いです。
その剰余算した結果が小数点以下第 1 桁の値(0 or 1)となります。
ただし、ここで行いたいのは「整数部に対する剰余算」であることに注意です。
これを行うためには、小数点以下を含む実数の整数部だけを取り出し、その取り出した整数部に対して剰余算を行う必要があります。
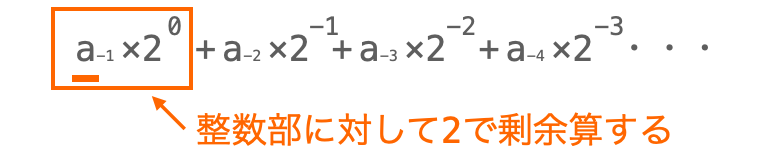
C言語では、整数部のみを取り出すためには単純に整数型の型にその実数を格納すれば良いです。
float value;
int int_value;
value = 0.5625;
value = 2 * value;
int_value = value; /* int_value == 1 */スポンサーリンク
後は掛け算と剰余算を繰り返せば良いだけ
先程は 2 の -1 乗の項の係数、つまり2進数変換した時の小数点以下第 1 桁を求めましたが、次は小数点以下第 2 桁を求めることを考えてみましょう。
先程、2進数変換しようとしている元々の小数点以下の値に対して 2 を掛けました。
この値を2の冪乗の和で表して考えると、各項の冪数が全て +1 されたことになります。
したがって、最初 2 の -2 乗だった項は現段階では 2 の -1 乗の項になっています(この項の係数は2進数変換した時に少数点以下第 2 桁の値になります)。
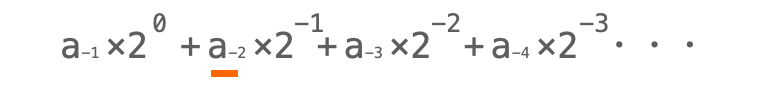
つまり、もう一回 2 を掛けてやれば全ての項の冪数が +1 され、元々 2 の -2 乗だった項を 2 の 0 乗にすることができます。

後は小数点以下第 1 桁の時と同様に剰余算してやれば、小数点以下第 2 桁の値を求めることができます。
これと同様に、さらにもう一度 2 を掛けて剰余算を行うことで小数点以下第 3 桁をの値を、さらにもう一度 2 を掛けて剰余算を行うことで小数点以下第 4 桁の値を求めることができます。
こんな感じで2進数に変換したい小数点以下の値に対し、下記を繰り返すことで2進数の各桁を求めることができます。つまり小数点以下の値を2進数に変換することができます。
2を掛ける2で剰余算する

なるほどなー
割り算じゃなくて掛け算を使えば小数点以下の値の2進数変換ができるんだね!
まあどちらも2の冪乗の冪数を増減させるという観点で考えるとどちらも同じだね!
やり方を忘れた時は、整数部も小数部も2の冪乗の和で表せることを思い出そう!

繰り返すのは小数点以下が 0 になるまで
どれだけ繰り返せば良いかですが、基本的には 2 を掛けた結果の小数点以下の値が 0 になるまで繰り返せば良いです。
元々の値に1度 2 を掛けると冪数が +1 されることになります。
これはつまり、小数点以下の1桁分が整数部に移動するということになります。

したがって、2 での掛け算を繰り返すたびに小数点以下の値がどんどん小さくなっていきます(代わりに整数部の値がどんどん大きくなっていきます)。
そして、そのうち小数点以下の値が 0 になります。つまり、冪数がマイナスの2の冪乗の項がなくなると言うことです。
この時は小数点以下の値を全て2進数に変換できたということになりますので繰り返しを終了して良いです。
あとは求めた係数を表示すれば、小数点以下の値を2進数変換した結果を表示することができます。
ただし、あくまでも 0 になっているかどうかを確認するのは「小数点以下の値」のみです。
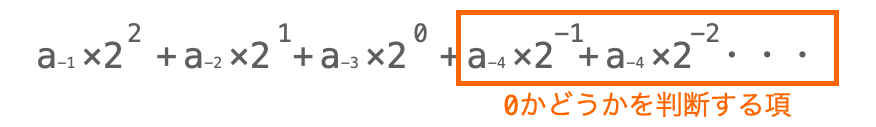
このやり方では、もともとは小数点以下の値を表す項を 2 を何回も掛けて整数部に移動させる(2 の 0 乗の項にする)ことで2進数変換を実現しています。
したがって、もともと小数点以下の値を表す項は、小数点以下の値を2進数変換できた時には整数部に移動していることになります。なので、整数部は基本的に 0 ではありません。
ですので、小数点以下の値のみを取得し、その取得した値が 0 であるかを確認するようにしましょう。
例えば、下記のようにして小数点以下の値のみを取得することができます。
float value;
int int_value;
float under_value;
value = 0.5625;
value = 2 * value;
int_value = value;
under_value = value - int_value; /* under_value == 0.125 */
2 を掛ければ2進数の「小数点の位置を右に1桁分移動」させられるの?まさにその通り!
2進数は 2 を掛けると小数点の位置が右に、2 で割ると小数点の位置が左に一桁分移動するよ
この辺りは浮動小数点数にも応用されているし、覚えておくといいと思うよ!

小数点以下の値を2進数変換するプログラム
ここまで解説してきた手順に基づいて作成したプログラムのソースコードは下記のようになります。
#include <stdio.h>
/* 最大桁数 */
#define MAX_BIT 1024
int main(void) {
float input; /* 2進数に変換する値 */
float value; /* inputの絶対値 */
float under_value; /* valueの小数点以下の値 */
int int_value; /* valueの整数部の値 */
unsigned int bin[MAX_BIT]; /* 小数点以下の2進数を格納 */
int i, j;
/* 2進数に変換したい小数点以下の値を代入 */
input = 0.5625;
/* 正の値に変換 */
if (input < 0) {
value = -input;
} else {
value = input;
}
i = 0;
while(i < MAX_BIT) {
/* 冪数を+1 */
value = value * 2;
/* 整数部分のみを取り出す */
int_value = value;
/* 剰余算で 2 の 0 乗の項の値を取得し、
小数点以下第 i + 1 桁の値として決定 */
bin[i] = int_value % 2;
/* 小数点以下の値のみを取り出す */
under_value = value - int_value;
/* 次の桁へ */
i++;
if (under_value == 0) {
/* 小数点以下が 0 なら終了 */
break;
}
}
if (input < 0) {
/* 負の値の場合は符号を表示 */
printf("-");
}
printf("0.");
for (j = 0; j < i; j++) {
printf("%u", bin[j]);
}
printf("\n");
return 0;
}実行すると下記のように input の小数点以下の値を2進数に変換した結果が表示されます。
0.1001
小数点以下の値を2進数変換し、変換後の各桁を配列 bin に格納しています。
小数点以下第 1 桁から順に配列 bin の先頭から格納しています。
一応負の値も対応させていますが、単に2進数変換した結果に - を付加して表示しているだけになります。
スポンサーリンク
まとめ
このページでは、10進数の小数点以下の値を2進数に変換する方法について解説しました。
「小数」と聞くと難しそうに感じるかもしれませんが、このページで解説した通り、整数の2進数変換と同様の方法で2進数に変換することが可能です。
具体的には下記の2つを繰り返すことで、10進数の小数点以下の値を2進数に変換することができます。
2の掛け算2での剰余算
今回紹介した方法やプログラムでなくても小数点以下の値を2進数に変換することは可能です。
また、整数の2進数変換と併せて考えれば、実数の2進数変換もできるようになります!
是非みなさんも、他にどのような方法で小数点以下の値を2進数変換できるかや、実数の2進数変換の方法やプログラムについて考えてみてください!
オススメの参考書(PR)
C言語学習中だけど分からないことが多くて挫折しそう...という方には、下記の「スッキリわかるC言語入門」がオススメです!
まず学習を進める上で、参考書は2冊持っておくことをオススメします。この理由は下記の2つです。
- 参考書によって、解説の仕方は異なる
- 読み手によって、理解しやすい解説の仕方は異なる
ある人の説明聞いても理解できなかったけど、他の人からちょっと違った観点での説明を聞いて「あー、そういうことね!」って簡単に理解できた経験をお持ちの方も多いのではないでしょうか?
それと同じで、1冊の参考書を読んで理解できない事も、他の参考書とは異なる内容の解説を読むことで理解できる可能性があります。
なので、参考書は2冊持っておいた方が学習時に挫折しにくいというのが私の考えです。
特に上記の「スッキリわかるC言語入門」は、他の参考書とは違った切り口での解説が豊富で、他の参考書で理解できなかった内容に対して違った観点での解説を読むことができ、オススメです。題名の通り「なぜそうなるのか?」がスッキリ理解できるような解説内容にもなっており、C言語入門書としてもかなり分かりやすい参考書だと思います。
もちろんネット等でも色んな観点からの解説を読むことが出来ますので、分からない点は別の人・別の参考書の解説を読んで解決していきましょう!もちろん私のサイトも参考にしていただけると嬉しいです!
入門用のオススメ参考書は下記ページでも紹介していますので、こちらも是非参考にしていただければと思います。
https://daeudaeu.com/c_reference_book/