【C言語】剰余演算（%）の使いどころ

このページにはプロモーションが含まれています

今回は剰余演算の使いどころについて説明していきたいと思います。

C言語においては剰余演算は % 演算子により実行することが可能です。この剰余演算は学校で習った四則演算には含まれません。四則演算は下記の４つであり、C言語においてはそれぞれ +・-・*・/ の演算子で実行することが可能です。そして、これらは四則演算であるだけあって非常に多くの場面で利用することになります。

加算（足し算）
減算（引き算）
乗算（掛け算）
除算（割り算）

で、前述の通り % で実行する剰余演算については四則演算には含まれません。そもそも学校の数学等の授業で余りを求める機会も少なかったのではないでしょうか？

ですが、プログラミングにおいては剰余演算を利用する機会が非常に多いです。

では、実際にどんな場面で剰余演算を利用する機会があるのか？この「剰余演算の使いどころ」について説明していきたいと思います。

Contents

単に余りを求める
除数未満の値に変換する
- 除数未満の乱数の生成を実現する
0 〜除数 - 1 の間を循環させる
- リングバッファーを実現する
まとめ

単に余りを求める

剰余演算の使いどころの１つ目は「単に余りを求めたい」場面になります。剰余演算は余りを求める演算ですので、単に余りを求めたい時も当然剰余演算を利用することになります。

例えば「リンゴが 1000 個あって、それを 15 人で均等に分けた場合にリンゴは何個余るでしょうか？みたいな問題を解きたい場合は剰余演算が活躍しますね！

余りを求める例

int r = 1000 / 15;
printf("%d\n", r);

剰余演算は余りを求める演算ですので、当然余りを求めることを目的に利用する機会は多いです。

除数未満の値に変換する

もう１つの使いどころは、値を「除数未満の値に変換したい」場合になると思います。

除数が正の数である場合、剰余演算の結果は必ず「除数未満」となります。除数とは割る方の数のことです（分母）。例えば下記を実行した場合、N が正の数であれば x の値に関わらず y の値は必ず N 未満となります。

y = x % N

この性質を利用して特定の値を除数未満の値に変換することを目的に剰余演算を利用することが多いです。

除数未満の乱数の生成を実現する

例えば、６面のサイコロの出目をランダムに取得するような処理について考えてみましょう！説明が簡単になるように、６面のサイコロの出目は 0 〜 5 であるとしたいと思います。このようなサイコロの出目をランダムに取得したいのであれば、0 〜 5 の乱数を生成して取得すれば良いことになります。

そして、C言語においては、乱数を取得するためには rand 関数が利用されます。ですが、rand 関数の返却値は 0 〜 RAND_MAX の範囲内のランダムな整数となり、私が利用しているコンパイラの場合は RAND_MAX は 2147483647 と定義されています。したがって、この場合の rand 関数の返却値の範囲は 0 〜 2147483647 となり、サイコロの目とは程遠い値が得られることになります。

で、このような場合に利用するのが剰余演算です。剰余演算を利用すれば rand 関数の返却値を除数未満の値に変換することが可能です。サイコロの目を得たいのであれば、rand 関数の返却値を 6 で剰余演算してやれば、その結果は必ず 0 〜 5 となります。そして、これにより、前述のサイコロの目のランダムな取得が実現できることになります。

サイコロの目の取得

#include <stdlib.h>

int dice(void) {
    return rand() % 6;
}

こんな感じで、”特定の値” を「除数未満の値に変換したい」ような場合には剰余演算が活躍します。

この剰余演算の良いところは、”特定の値” を循環させながら除数未満の値に変換できるという点になります。そしてこれにより、“特定の値” の特徴を保ったまま除数未満の値に変換させることが可能となります。

例えば、単に rand 関数の返却値を 6 未満の値に変換したいのであれば、これは剰余演算を利用しなくても rand 関数から 6 以上の値が返却された場合は全て強制的に 5 に置き換えることでも実現可能です。具体的には下記みたいな感じですね。

強制的な値の置き換え

#include <stdlib.h>

int dice(void)
{
    int ret = rand();
    if (ret >= 6) {
        ret = 5;
    }
    return ret;
}

確かに、これでもサイコロの目に相当する 0 〜 5 の値のみを取得可能な関数が実現できます。ですが、この場合、rand の結果が 5 〜 RAND_MAX の場合に全て 5 に置き換えられることになるため、rand の結果が 0 〜 4 の場合を除いて全てサイコロの目が 5 ということになってしまいます。つまり、極端に 5 の目が出やすいサイコロということになってしまい、rand 関数のランダム性が失われてしまうことになります。

ですが、剰余演算を利用した場合は rand 関数のランダム性を保ったまま除数未満の値への変換を実現することが可能です。これは剰余演算の結果が 0 〜 除数 - 1 の間を循環するからになります。

サイコロの目の例で考えれば、rand 関数の結果が 0 〜 5 の場合、剰余演算結果もそのまま 0 〜 5 となります。それに対し rand 関数の結果が 6 の場合は 0 〜 5 を１周回って 0 に、同様に 7 の場合は 0 〜 5 を１周回って 1 となります。12 の場合は 0 〜 5 を２周回って 0 となります。したがって、剰余演算の結果は rand 関数の返却値が 0 〜 除数 - 1 の間を循環する形で除数未満の値に変換されることになります。

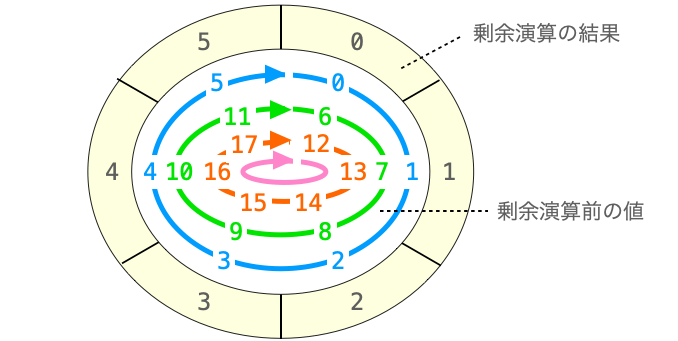
このように、循環する形で除数未満の値に変換されるため、剰余演算の場合は元々の “特定の値” の性質をある程度保ったまま “特定の値” を除数未満に変換することが可能となります。rand 関数の剰余演算結果は、rand 関数のランダム性を保ったまま除数未満の値に変換することができ、これにより均等に目が出るサイコロを実現することができることになります。

このように、”特定の値” の性質を保ったまま除数未満の値に変換したい場合に剰余演算が活躍することになります。

ちなみに、rand 関数については下記ページで解説していますので、rand 関数について詳しく知りたい方は下記ページをご参照ください。本当は srand 関数と組み合わせて使用する必要があるのですが、今回は簡単のため srand 関数の利用は省略しています。

C言語で乱数を扱う方法（rand関数とsrand関数）

`0` 〜 `除数 - 1` の間を循環させる

先ほどの説明と重複する部分もありますが、剰余演算は「値を 0 〜 除数 - 1 の間で循環させる」ことを目的に利用することも多いです。例えばリングバッファーを実現する際にも剰余演算が利用されます。

リングバッファーを実現する

リングバッファーとは、リングのように、バッファーの終端と始端が繋がっているようなバッファーとなります。バッファー = 配列として考えてもらって良いです。

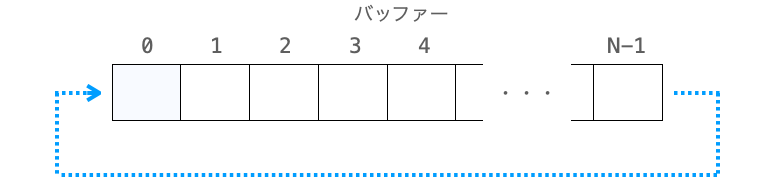
例えばですが、バッファーの先頭から順々にデータを格納する場合、バッファーがサイズ N の配列であれば添字 0 の位置から順々にデータを格納していき添字が N になった場合に先頭に戻って添字 0 の位置にデータが格納されることになります（図では矢印がデータ格納位置を示しています）。

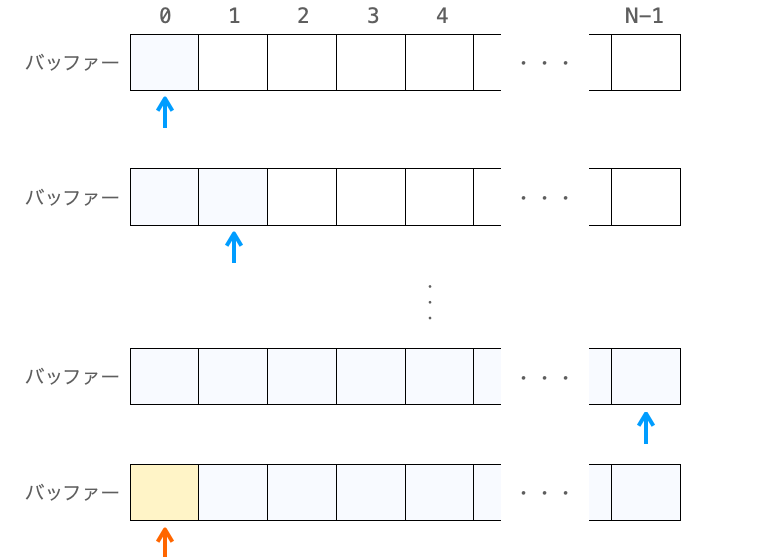
このように、リングバッファーを扱う際は配列の添字が N (配列のサイズ) 以上になった場合に先頭にまた戻すという処理が必要になり、添字の扱いが難しいです。例えば添字の扱いを誤ってしまって配列外にアクセスするようなことがあるとプログラムが異常終了してしまう場合もあります。

ですが、このような添字の扱いも剰余演算を利用すれば楽々実現することが可能です。上記のようなデータの格納を実現するのであれば、配列の添字を扱う変数に対して N での剰余演算を実施してやれば良いだけになります。これにより、配列の添字が自動的に 0 〜 N - 1 の間を循環するようになります。

こうすれば、配列の添字は必ず N 未満の値になって配列外にデータが格納されることを防ぐことができます。また、N になった際に自動的に先頭の 0 に循環して戻ることになり、添字を扱う変数の値が増えていっても添字は 0 〜 N - 1 の間を順々に循環することになり、あたかもバッファーの終端と始端とが繋がっているかのようにデータの格納位置が自動的に変化していくことになります。

リングバッファーを扱う具体的なプログラムのソースコードは下記のようになります。本当はデータを取得するような処理も必要になりますが、シンプルなソースコードにするためデータの格納のみを行うようにしています。

リングバッファーの実現

#include <stdio.h>

#define N 4

static int buffer[N];
static int i;

void print(void) {
    for (int j = 0; j < N; j++) {
        printf("%d, ", buffer[j]);
    }
    printf("\n");
}

void put(int data) {
    buffer[i] = data;
    i = (i + 1) % N;
}

int main(void) {
    i = 0;

    put(0);
    print();

    put(1);
    print();

    put(2);
    print();

    put(3);
    print();

    put(4);
    print();

    for (int j = 0; j < 100; j++) {
        put(j + 4);
        print();
    }
}

バッファーへのデータの格納位置は変数 i で管理しており、この i を増加させる際に i = (i + 1) % N; の計算を行なっているため、変数 i の値は必ず N 未満になりますし、i + 1 が N になった際には自動的に先頭の 0 に戻るようになっています。

このリングバッファーはデータ構造の１つである「キュー」を配列で実現する際等に利用することが多いです。キューについては下記ページで解説しており、実際にリングバッファーを利用する例も示していますので、興味があれば読んでみてください。

【C言語/データ構造】スタックとキューの配列での実装方法

こんな感じで、プログラミングをしていれば、余りを求めるだけでなく「特定の値を除数未満に変換したい」ケースや「値を 0 〜 除数 - 1 の間で循環させたい」ケースに多く遭遇すると思います。そんな時には剰余演算が利用できないかどうかを検討してみると良いと思います！

まとめ

このページでは剰余演算の使いどころについて説明しました！

ご存知の通り、剰余演算は余りを求めるための演算で、単に余りを求めることを目的とする場合だけではなく、特定の値を除算未満の値に変換することを目的とした場合や、値を 0 〜 除数 - 1 の間で循環させたいような場合にも活躍する演算になります。

四則演算ではないものの、特にプログラミングにおいては四則演算と並ぶ非常に重要な演算となりますので、剰余演算の特徴については理解しておきましょう！

今回は特に正の値に対する剰余演算について説明していますが、負の値に対する剰余演算に関しては剰余演算結果の符号に注意が必要となります。この点については下記ページで解説していますので、剰余演算についてもっと詳しく知りたい方は是非下記ページも読んでみてください！

【C言語】負の値に対する剰余演算の結果まとめ

オススメの参考書（PR）

C言語学習中だけど分からないことが多くて挫折しそう...という方には、下記の「スッキリわかるC言語入門」がオススメです！

スッキリわかるC言語入門第2版

posted with ヨメレバ

中山清喬/株式会社フレアリンクインプレス 2021年12月14日頃

楽天ブックス

Amazon

Kindle

まず学習を進める上で、参考書は２冊持っておくことをオススメします。この理由は下記の２つです。

参考書によって、解説の仕方は異なる
読み手によって、理解しやすい解説の仕方は異なる

ある人の説明聞いても理解できなかったけど、他の人からちょっと違った観点での説明を聞いて「あー、そういうことね！」って簡単に理解できた経験をお持ちの方も多いのではないでしょうか？

それと同じで、１冊の参考書を読んで理解できない事も、他の参考書とは異なる内容の解説を読むことで理解できる可能性があります。

なので、参考書は２冊持っておいた方が学習時に挫折しにくいというのが私の考えです。

特に上記の「スッキリわかるC言語入門」は、他の参考書とは違った切り口での解説が豊富で、他の参考書で理解できなかった内容に対して違った観点での解説を読むことができ、オススメです。題名の通り「なぜそうなるのか？」がスッキリ理解できるような解説内容にもなっており、C言語入門書としてもかなり分かりやすい参考書だと思います。

もちろんネット等でも色んな観点からの解説を読むことが出来ますので、分からない点は別の人・別の参考書の解説を読んで解決していきましょう！もちろん私のサイトも参考にしていただけると嬉しいです！

入門用のオススメ参考書は下記ページでも紹介していますので、こちらも是非参考にしていただければと思います。