2次元高速フーリエ変換を実装しようと思ったのですがいきなり高速フーリエ変換、しかも2次元!となると難易度高いので順を追って1次元離散フーリエ変換から実装して力をつけていくことにしました…。
1次元離散フーリエ変換
いきなり1次元離散フーリエ変換のプログラムに移る前に、まずは実装しやすい形に1次元離散フーリエ変換の公式を変化させていきたいと思います。
1次元離散フーリエ変換の公式は下記の通りになります。データのサンプル数は M 個とし、m は -M/2 から M/2 - 1 まで変化する実空間の変数、u は周波数空間の変数としています。
$$ F(u) = \sum_{m = -M/2}^{M/2 – 1} f(m) e^{-i \frac{2 \pi u m}{M}} $$
上記の計算をすべての u に関して求める処理が離散フーリエ変換となります。複素数が混じっているところが厄介ですね。C言語では扱いにくい…。
なので、オイラーの公式を適用して、実数部と虚数部を分けて考えます。
$$ F(u) = \sum_{m = -M/2}^{M/2 – 1} f(m) \cos ( \frac{2 \pi u m}{M} ) + i \sum_{m = -M/2}^{M/2 – 1} f(m) \sin ( \frac{2 \pi u m}{M} ) $$
上式を変化させれば、実数部 \( Re[F(u)] \)と虚数部 \( Im[F(u)] \)はそれぞれ下記の式で求めることが可能です。
$$ Re[F(u)] = \sum_{m = -M/2}^{M/2 – 1} f(m) \cos ( \frac{2 \pi u m}{M} ) $$
$$ Im[F(u)] = – \sum_{m = -M/2}^{M/2 – 1} f(m) \sin ( \frac{2 \pi u m}{M} ) $$
\( F(u) \)は実数部 \( Re[F(u)] \)と虚数部 \( Im[F(u)] \)を用いて下記の式で表すことが可能です。
$$ F(u) = Re[F(u)] + i * Im[F(u)] $$
1次元逆離散フーリエ変換
逆離散フーリエ変換の公式は下記の通りです。離散フーリエ変換のときと同様に式を整理していきましょう!逆変換ではuに関して総和を求めていく計算になります。
$$ f(m) = \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} F(u) e^{i \frac{2 \pi u m}{M}} $$
こちらをすべてのmに対して計算すれば逆変換は完了です。
オイラーの公式適用で下記になります。
$$ f(m) = \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} F(u) \cos ( \frac{2 \pi u m}{M} ) + i \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} F(u) \sin ( \frac{2 \pi u m}{M} ) $$
さらに、ここで離散フーリエ変換のときに求めた実数部 \( Re[F(u)] \)と虚数部 \( Im[F(u)] \)を\( F(u) \)に代入して式を整理すると下記のようになります。
$$ f(m) = \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} \bigl[ Re[F(u)] \cos ( \frac{2 \pi u m}{M} ) + i * Im[F(u)] \cos ( \frac{2 \pi u m}{M} ) \bigr] \\+ i \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} \bigl[ Re[F(u)] \sin ( \frac{2 \pi u m}{M} ) + i * Im[F(u)] \sin ( \frac{2 \pi u m}{M} ) \bigr] $$
さらにこれを整理してやれば次のようになります。i * i = -1 の計算を実行していることに注意です。
$$ f(m) = \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} \bigl[ Re[F(u)] \cos ( \frac{2 \pi u m}{M} ) – Im[F(u)] \sin ( \frac{2 \pi u m}{M} ) \bigr] \\+ i \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} \bigl[ Re[F(u)] \sin ( \frac{2 \pi u m}{M} ) + Im[F(u)] \cos ( \frac{2 \pi u m}{M} ) \bigr] $$
以上より逆離散フーリエ変換後の実数部 \( Re[f(m)] \)と虚数部 \( Im[f(m)] \)はそれぞれ下記の式で求めることが可能です。
$$ Re[f(m)] = \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} \bigl[ Re[F(u)] \cos ( \frac{2 \pi u m}{M} ) – Im[F(u)] \sin ( \frac{2 \pi u m}{M} ) \bigr] $$
$$ Im[f(m)] = \frac{1}{M} \sum_{u = -M/2}^{M/2 – 1} \bigl[ Re[F(u)] \sin ( \frac{2 \pi u m}{M} ) + Im[F(u)] \cos ( \frac{2 \pi u m}{M} ) \bigr] $$
実数部 \( Re[f(m)] \)と虚数部 \( Im[f(m)] \)を用いれば逆離散フーリエ変換結果 \( f(m) \)は下記で表すことが可能です。
$$ f(m) = Re[f(m)] + i * Im[f(m)] $$
スポンサーリンク
プログラム
#include <math.h>
#define PI 3.141592653
#define M 8192 /* サンプル数 */
int main(int argc, char *argv[]){
int m; /* 実空間データ走査用の添字 */
int u; /* 周波数空間データ走査用の添字 */
double *rdata, *idata;
double rsum, isum;
unsigned int ulen;
double *data, *outidata, *outrdata;
char outname[256];
FILE *fo;
data = (double*)malloc(sizeof(double) * M);
/* 入力データ作成 */
for(m = 0; m < M; m++){
if((m < M / 8) || (m >= 3 * M / 8 && m < 5 * M / 8) || (m >= 7 * M / 8)){
data[m] = 1;
}else{
data[m] = 0;
}
}
ulen = M;
/* DFT後の実数部と虚数部格納用のメモリ確保 */
rdata = (double*)malloc(sizeof(double) * ulen);
if(rdata == NULL){
printf("malloc rdata error\n");
return -1;
}
idata = (double*)malloc(sizeof(double) * ulen);
if(idata == NULL){
printf("malloc idata error\n");
free(rdata);
return -1;
}
/* 離散フーリエ変換実行 */
for(u = 0; u < ulen; u++){
rsum = 0;
isum = 0;
for(m = 0; m < M; m++){
/* M/2を原点として考えている */
rsum += data[m] * cos(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M));
isum -= data[m] * sin(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M));
}
rdata[u] = rsum;
idata[u] = isum;
}
/* フィルタ処理 */
/* ここではローパスフィルタをかけている */
for(u = 0; u < ulen; u++){
/* M/2を原点として考えている */
if(u < M / 4 || u >= 3 * M / 4){
rdata[u] = 0;
idata[u] = 0;
}
}
/* 逆フーリエ変換後の実数部と虚数部を格納するメモリ確保 */
outrdata = (double*)malloc(sizeof(double) * M);
if(outrdata == NULL){
printf("malloc data error\n");
free(data);
free(rdata);
free(idata);
return -1;
}
outidata = (double*)malloc(sizeof(double) * M);
if(outidata == NULL){
printf("malloc data error\n");
free(data);
free(rdata);
free(idata);
free(outrdata);
return -1;
}
/* 逆離散フーリエ変換実行 */
for(m = 0; m < M; m++){
rsum = 0;
isum = 0;
for(u = 0; u < ulen; u++){
/* M/2を原点として考えている */
rsum += (rdata[u] * cos(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M))
- idata[u] * sin(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M)));
isum += (idata[u] * cos(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M))
+ rdata[u] * sin(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M)));
}
outrdata[m] = rsum / M;
outidata[m] = isum / M;
}
/* データ出力 */
/* 振幅スペクトラム */
sprintf(outname, "%s", "1dft.txt");
fo = fopen(outname, "w");
for(u = 0; u < ulen; u++){
fprintf(fo, "%.1f\n", sqrt(rdata[u] * rdata[u] + idata[u] * idata[u]));
}
fclose(fo);
/* 入力データ */
sprintf(outname, "%s", "indata.txt");
fo = fopen(outname, "w");
for(m = 0; m < M; m++){
fprintf(fo, "%.1f\n",data[m]);
}
fclose(fo);
/* 逆離散フーリエ変換後の実数部 */
sprintf(outname, "%s", "outrdata.txt");
fo = fopen(outname, "w");
for(m = 0; m < M; m++){
fprintf(fo, "%.1f\n",outrdata[m]);
}
fclose(fo);
/* 逆離散フーリエ変換後の虚数部 */
sprintf(outname, "%s", "outidata.txt");
fo = fopen(outname, "w");
for(m = 0; m < M; m++){
fprintf(fo, "%.1f\n",outidata[m]);
}
fclose(fo);
free(data);
free(rdata);
free(idata);
free(outrdata);
free(outidata);
return 0;
}
プログラムの流れ
プログラムの流れは下記のようになっています。
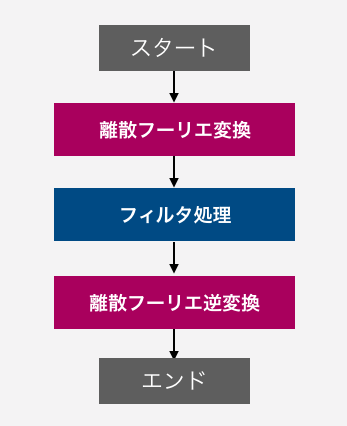
プログラム説明
スポンサーリンク
入力データ作成
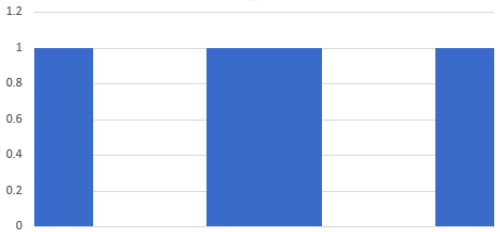
今回は下記のようなM/4ごとに1と0が反転するような矩形データを入力データとしました。
/* 入力データ作成 */
for(m = 0; m < M; m++){
if((m < M / 8) || (m >= 3 * M / 8 && m < 5 * M / 8) || (m >= 7 * M / 8)){
data[m] = 1;
}else{
data[m] = 0;
}
}1次元離散フーリエ変換実行
1次元離散フーリエ変換は下記で行なっています。実数部 \( Re[F(u)] \)をrdata[u]、虚数部 \( Im[F(u)] \)をidata[u]として扱っています。
/* 離散フーリエ変換実行 */
for(u = 0; u < ulen; u++){
rsum = 0;
isum = 0;
for(m = 0; m < M; m++){
/* M/2を原点として考えている */
rsum += data[m] * cos(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M));
isum -= data[m] * sin(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M));
}
rdata[u] = rsum;
idata[u] = isum;
}フィルタ処理
フィルタ処理も行ってみました。
ここでは低い周波数の成分のみ残し、高周波成分はカットするローパスフィルターをかけています。これにより、逆変換結果では入力データに比べてデータの変化が滑らになることが期待できます。
/* フィルタ処理 */
/* ここではローパスフィルタをかけている */
for(u = 0; u < ulen; u++){
/* M/2を原点として考えている */
if(u < M / 4 || u >= 3 * M / 4){
rdata[u] = 0;
idata[u] = 0;
}
}スポンサーリンク
1次元逆離散フーリエ変換実行
フィルタ処理後のデータに対して下記で1次元逆離散フーリエ変換を実行しています。
上の方で示した1次元逆離散フーリエ変換後の実数部と虚数部を得るための式がここで現れています。プログラムでは実数部\( Re[f(m)] \)をoutrdata[m]、虚数部 \( Im[f(m)] \)をoutidata[m]として扱っています。
/* 逆離散フーリエ変換実行 */
for(m = 0; m < M; m++){
rsum = 0;
isum = 0;
for(u = 0; u < ulen; u++){
/* M/2を原点として考えている */
rsum += (rdata[u] * cos(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M))
- idata[u] * sin(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M)));
isum += (idata[u] * cos(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M))
+ rdata[u] * sin(2 * PI * ((u - ulen / 2) * (m - M / 2) / (double)M)));
}
outrdata[m] = rsum / M;
outidata[m] = isum / M;
}結果
・入力データ
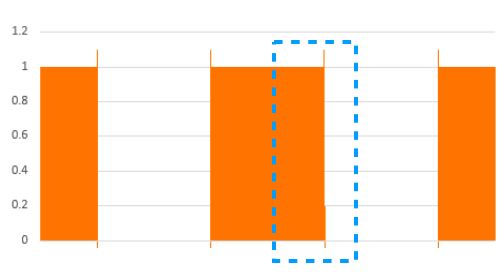
・出力データ
これで合ってんのか?っていう感じの結果ですね…。正解が無いからなんとも言えない…。
・比較
ただ出力結果の青枠で囲ったようなエッジ部分を見てみるとたしかに変換が滑らかになりローパスフィルターの効果があわられていることが確認できました。
ローパスフィルターのカットさせる領域をもっと増やせばもっとわかりやすい結果になったかもしれませんが…。
オススメの参考書(PR)
C言語学習中だけど分からないことが多くて挫折しそう...という方には、下記の「スッキリわかるC言語入門」がオススメです!
まず学習を進める上で、参考書は2冊持っておくことをオススメします。この理由は下記の2つです。
- 参考書によって、解説の仕方は異なる
- 読み手によって、理解しやすい解説の仕方は異なる
ある人の説明聞いても理解できなかったけど、他の人からちょっと違った観点での説明を聞いて「あー、そういうことね!」って簡単に理解できた経験をお持ちの方も多いのではないでしょうか?
それと同じで、1冊の参考書を読んで理解できない事も、他の参考書とは異なる内容の解説を読むことで理解できる可能性があります。
なので、参考書は2冊持っておいた方が学習時に挫折しにくいというのが私の考えです。
特に上記の「スッキリわかるC言語入門」は、他の参考書とは違った切り口での解説が豊富で、他の参考書で理解できなかった内容に対して違った観点での解説を読むことができ、オススメです。題名の通り「なぜそうなるのか?」がスッキリ理解できるような解説内容にもなっており、C言語入門書としてもかなり分かりやすい参考書だと思います。
もちろんネット等でも色んな観点からの解説を読むことが出来ますので、分からない点は別の人・別の参考書の解説を読んで解決していきましょう!もちろん私のサイトも参考にしていただけると嬉しいです!
入門用のオススメ参考書は下記ページでも紹介していますので、こちらも是非参考にしていただければと思います。
https://daeudaeu.com/c_reference_book/