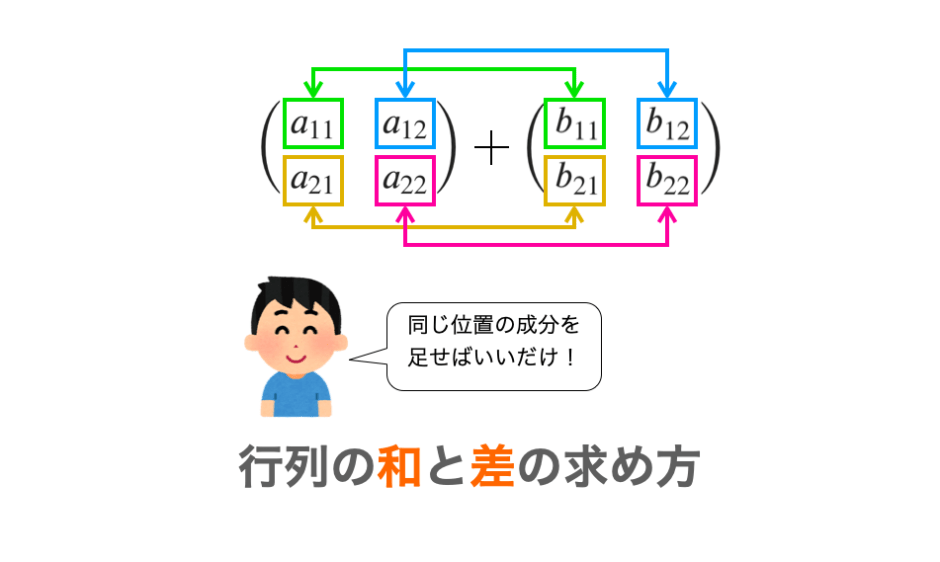
このページでは、C言語での「行列の和」及び「行列の差」の求め方について解説していきます。
C言語での行列の扱い方については下記ページで解説していますので、そもそもC言語で行列を扱う方法をご存知ない方は、事前に下記ページを読んでいただくことをオススメします。
 【C言語】行列の扱い方
【C言語】行列の扱い方
Contents
行列の和の求め方
それでは、C言語での行列の和の求め方について解説していきます。
同じ位置の要素の足し算を行う
下記の2行3列の2つの行列 \(A\) と \(B\) の和をどうやって求めれば良いのかについて考えていきたいと思います。
$$ A = \left ( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{array} \right ) $$
$$ B = \left ( \begin{array}{ccc} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{array} \right ) $$
これらの行列 \(A\) と行列 \(B\) の和の結果となる行列を下記の行列 \(C\) とした場合、
$$ C = \left ( \begin{array}{ccc} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \end{array} \right ) $$
行列 \(C\) の各成分は下記のようにして求めることができます。
$$ \left ( \begin{array}{ccc} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \end{array} \right ) = \left ( \begin{array}{ccc} a_{11} + b_{11} & a_{12} + b_{12} & a_{13} + b_{13} \\ a_{21} + b_{21} & a_{22} + b_{22} & a_{23} + b_{23} \end{array} \right ) $$
つまり、行列の各成分 \(c_{i j}\) は、\(a_{i j}\) と \(b_{i j}\) を足し合わせることで求めることができます。この成分を全て計算してやれば、行列 \(C\) を求めることができます。
これは、行列 \(A\) と行列 \(B\) の”同じ位置の成分” 同士を足し合わせた結果が、行列 \(C\) における “同じ位置の成分” となると言い換えることができます。
また、下記のページで解説しているとおり、
 【C言語】行列の扱い方
【C言語】行列の扱い方
matA と matB を下記のように作成すれば、matA と matB における同じ添字の要素は行列内の同じ位置の成分であることになります。
matA:上記の行列 \(A\) を扱う2次元配列matA[i][j]に行列 \(A\)の成分 \(a_{i+1 j+1}\) を格納する
matB:上記の行列 \(B\) を扱う2次元配列matB[i][j]に行列 \(B\)の成分 \(b_{i+1 j+1}\) を格納する
このように作成した matA と matB を図示すれば、次のようなものになります。
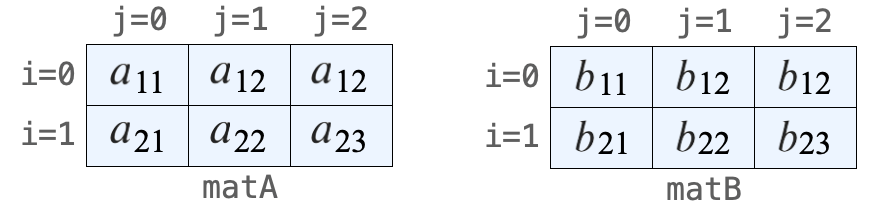
つまり、matC を上記の行列 \(C\) を扱う2次元配列とすれば、matC[i][j] は下記により求まることになります。
matC[i][j] = matA[i][j] + matB[i][j];上記により、行列 \(A\) と行列 \(B\) の和を表す行列 \(C\) における、成分 \(c_{i+1 j+1}\) が求まったことになります。
スポンサーリンク
“同じ位置の要素の足し算” を全ての位置に対して行う
ただし、上記で求まるのは行列 \(C\) の1つの成分のみですので、行列の和である行列 \(C\) を求めるためには、上記の計算を行列内の全ての成分に対して繰り返し行う必要があります。
また、行列 \(C\) の行数・列数は行列 \(A\) の行数・列数と同じになります(行列 \(B\) も同じ行数・列数である必要がある)。
したがって、j を 0から 行列 A の列数 - 1 まで変化させながら上記のように matC[i][j] を求めれば、行列 \(C\) の1行分の成分が求まることになります。
さらに、この1行分の成分を求める処理を、i を 0 から 行列 A の行数 - 1 まで変化させながら繰り返せば、全ての成分が求まり、行列 \(A\) と行列 \(B\) の和を求めることができることになります。
具体的には、行列 \(A\) と行列 \(B\) はともに2行3列の行列ですので、下記のようなループ処理を行えば良いことになります。
/* matAとmatBの和を求める */
for (i = 0; i < 2; i++) {
for (j = 0; j < 3; j++) {
matC[i][j] = matA[i][j] + matB[i][j];
}
}行列 \(A\) と行列 \(B\) が M 行 N 列の行数である場合は、下記のように M * N 個分の成分が求まるようにループを組めば良いことになります。
/* matAとmatBの和を求める */
for (i = 0; i < M; i++) {
for (j = 0; j < N; j++) {
matC[i][j] = matA[i][j] + matB[i][j];
}
}行列の和を計算する上で重要なのは「同じ位置の成分同士を足し合わせること」くらいです。
ただし、同じ位置の成分同士を足し合わせられないと行列の和を求めることができませんので、和を求めるためには2つの行列の行数と列数が同じである必要があります。
行列の和を求めるプログラムの例
ここまで説明した考え方に基づいて作成した「2つの行列の和」を求めるプログラムの例は下記のようになります。
#include <stdio.h>
#define M 2 /* 行列の行数 */
#define N 3 /* 行列の列数 */
int main(void) {
/* 1つ目のM行N列の行列を作成 */
int matA[M][N] = {
{1, 2, 3},
{4, 5, 6}
};
/* 2つ目のM行N列の行列を作成 */
int matB[M][N] = {
{7, 8, 9},
{10, 11, 12}
};
/* matAとmatBの行列の和となる行列 */
int matC[M][N];
int i, j;
/* matAとmatBの和を求める */
for (i = 0; i < M; i++) {
for (j = 0; j < N; j++) {
matC[i][j] = matA[i][j] + matB[i][j];
}
}
/* matAとmatBの和を表示 */
for (i = 0; i < M; i++) {
for (j = 0; j < N; j++) {
printf("%d,", matC[i][j]);
}
printf("\n");
}
return 0;
}このソースコードのプログラムを実行すれば、結果として下記が表示されることになります。
8,10,12, 14,16,18,
上記のソースコードでは、次の2つの行列の和を求めており、期待した通りの結果が表示されていることが確認できると思います。
$$ A = \left ( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array} \right ) $$
$$ B = \left ( \begin{array}{ccc} 7 & 8 & 9 \\ 10 & 11 & 12 \end{array} \right ) $$
行列の行数と列数は下記で定義しており、ここを変更すれば、様々な行数・列数の行数の和を求めることができます。
#define M 2 /* 行列の行数 */
#define N 3 /* 行列の列数 */ただし、行列の行数や列数を変更した場合、和を求める前に matA と matB に格納しておく必要のある成分数も変わるので注意してください。
行列として扱う2次元配列への値の格納に関しては下記ページで解説していますので、詳しくは下記ページを参照していただければと思います。
 【C言語】行列の扱い方
【C言語】行列の扱い方
行列の差の求め方
続いて、C言語での「行列の差」の求め方について解説していきます。
行列の和が求めることができるようになれば、行列の差は簡単に求めることができます。
スポンサーリンク
行列の和での足し算を引き算に変更するだけ
行列の差は、行列の和で足し算していたところを「引き算に変えてやるだけ」で求めることができます。
具体的には、下記の2行3列の2つの行列 \(A\) と \(B\) の差の結果は、
$$ A = \left ( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{array} \right ) $$
$$ B = \left ( \begin{array}{ccc} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{array} \right ) $$
下記のようになります。
$$ C = \left ( \begin{array}{ccc} a_{11} – b_{11} & a_{12} – b_{12} & a_{13} – b_{13} \\ a_{21} – b_{21} & a_{22} – b_{22} & a_{23} – b_{23} \end{array} \right ) $$
つまり、各成分の計算は、行列の和を求める時に実行していた下記の処理を、
matC[i][j] = matA[i][j] + matB[i][j];下記のように変更すれば良いだけになります。
matC[i][j] = matA[i][j] - matB[i][j];行列の差を求めるプログラムの例
ここまで説明した考え方に基づいて作成した「2つの行列の差」を求めるプログラムのソースコード例は下記のようになります。
行列の和を求めるプログラムの例 で示したソースコードとの違いは、前述で示した箇所のみとなります(コメントはもうちょっと変更しています)。
#include <stdio.h>
#define M 2 /* 行列の行数 */
#define N 3 /* 行列の列数 */
int main(void) {
/* 1つ目のM行N列の行列を作成 */
int matA[M][N] = {
{1, 2, 3},
{4, 5, 6}
};
/* 2つ目のM行N列の行列を作成 */
int matB[M][N] = {
{7, 8, 9},
{10, 11, 12}
};
/* matAとmatBの行列の差となる行列 */
int matC[M][N];
int i, j;
/* matAとmatBの差を求める */
for (i = 0; i < M; i++) {
for (j = 0; j < N; j++) {
matC[i][j] = matA[i][j] - matB[i][j];
}
}
/* matAとmatBの差を表示 */
for (i = 0; i < M; i++) {
for (j = 0; j < N; j++) {
printf("%d,", matC[i][j]);
}
printf("\n");
}
return 0;
}このソースコードのプログラムを実行すれば、結果として下記が表示されることになり、2つの行列の差が求められていることが確認できると思います。
-6,-6,-6, -6,-6,-6,
行数や列数の変更方法に関しても 行列の和を求めるプログラムの例 と同じとなります。
まとめ
このページでは、「2つの行列の和」と「2つの行列の差」を求める方法について解説しました。
2つの行列の和は、お互いの行列の同じ位置の成分を足し合わせていくことで求めることができます。
また、2つの行列の和を実現できれば、あとは足し算を引き算に変更してしまえば、2つの行列の差を求めることもできます。
要は、2つの2次元配列の同じ添字の要素に対して足し算 or 引き算を行えば良いだけですので、割と簡単に実装できるとは思います。ただ、多重ループなどに慣れていないと戸惑うこともあると思いますので、多重ループが苦手な人にとっては、プログラミングの良い練習題材ではあると思います!
「行列の積」を求め方については下記ページで解説していますので、積の求め方を知りたい方は是非下記ページも読んでみてください!行列の積は、和や差に比べると実装の難易度は高いです!
 【C言語】行列の積の求め方
【C言語】行列の積の求め方