このページでは、C言語での「行列式の求め方」について解説していきます。
具体的には、下記の3つの正方行列に対する行列式の求め方について解説していきます。
- 1次正方行列
- 2次正方行列
- 3次正方行列
これらの行列式に関しては、行列式を求める計算式にそのまま行列の各成分を当てはめて計算すれば良いだけです。なので、計算式さえ思い出せれば簡単にプログラム化できます。
そのため、このページでは、行列式の計算式のおさらいと、C言語のプログラム例の紹介のみを行なっていきたいと思います。
4次以上の正方行列の行列式を扱うについてはちょっと難しいですので、別途ページを設けて解説させていただこうと思います。
また、C言語での行列の扱い方については下記ページで解説していますので、そもそもC言語で行列を扱う方法をご存知ない方は、事前に下記ページを読んでいただくことをオススメします。
 【C言語】行列の扱い方
【C言語】行列の扱い方
Contents
行列式の計算式
まず、行列式の計算式についておさらいしていきたいと思います。
1次正方行列の行列式
1次正方行列の場合は成分が1つのみであり、その成分そのものが行列式となります。
$$ \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a11 \end{vmatrix} = a11 $$
スポンサーリンク
2次正方行列の行列式
2次正方行列の各成分を下記の行列 \(A\) のように \(a_{ij}\) と表した場合、
$$ A = \left ( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right ) $$
2次正方行列の行列式は下記の計算式により求めることができます。
$$ \begin{vmatrix} A \end{vmatrix} = a_{11} a_{22} – a_{12} a_{21} $$
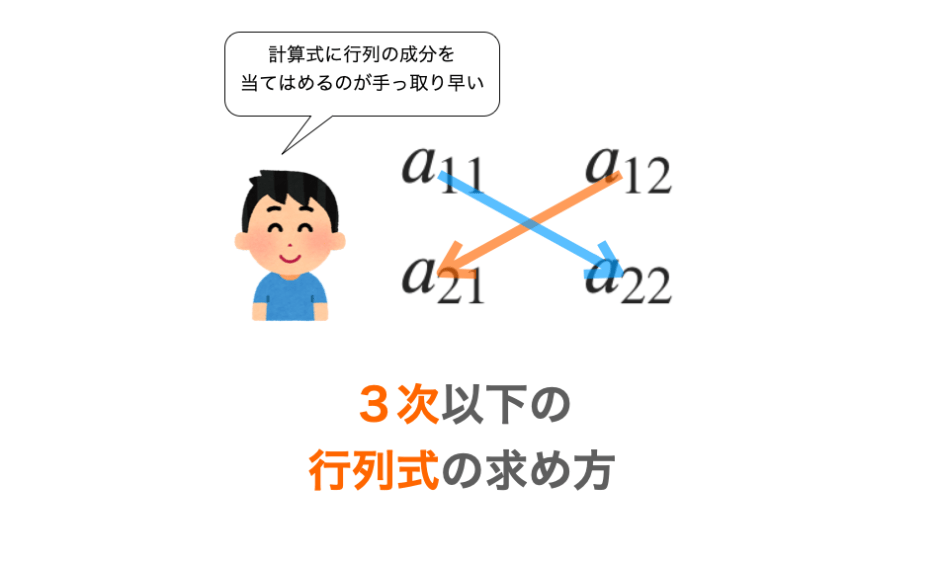
下の図のように、一番上の行の成分から右下方向に伸びる線と左下方向に伸びる線を考えると分かりやすいと思います。

「右下方向の線上の成分同士を掛け合わせた値」から「左下方向の線上の成分同士を掛け合わせた値」を引くことで、2次の正方行列の行列式を求めることができます。
3次正方行列の行列式
3次正方行列の各成分を下記の行列 \(A\) のように \(a_{ij}\) と表した場合、
$$ A = \left ( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right ) $$
3次正方行列の行列式は下記の計算式により求めることができます。
$$ \begin{vmatrix} A \end{vmatrix} = a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} – a_{11} a_{23} a_{32} – a_{12} a_{21} a_{33} + a_{13} a_{22} a_{31} $$
2次の行列式の計算時同様、下の図のように一番上の行の成分から右下方向に伸びる線と左下方向に伸びる線を考えると分かりやすいと思います(右側に行列のコピーを追加して考えています)。
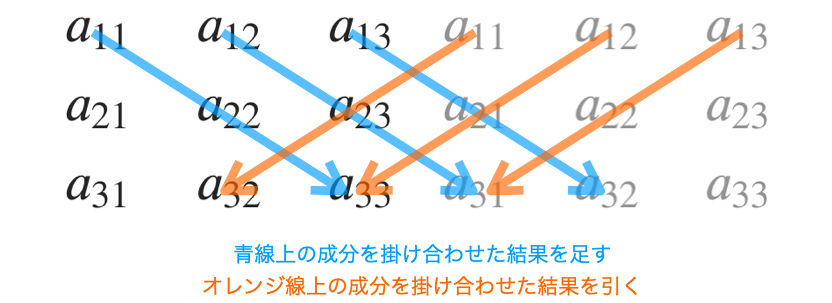
「右下方向の線上の成分同士を掛け合わせた値」を足し合わせた結果から「左下方向の線上の成分同士を掛け合わせた値」を足し合わせた結果を引くことで、3次の正方行列の行列式を求めることができます。
行列式を求めるプログラムの例
C言語で行列式を求める際には、行列の各成分をここまで紹介してきた計算式に当てはめて計算させれば良いだけです。
ただし、行列式の計算式 の場合は成分の位置を示す添字が \(1\) から始まるのに対し、C言語で扱う配列の添字が 0 から始まる点にのみ注意が必要だと思います。
スポンサーリンク
1次正方行列の行列式を求めるプログラム
まず1次正方行列の行列式を求めるプログラムは下記となります。この場合、成分が1つのみになるので計算を行わなくても行列式を求めることができます。
#include <stdio.h>
int main(void) {
/* 1次正方行列 */
int matA[1][1] = {
{5}
};
int determinant;
/* 行列式は成分そのもの */
determinant = matA[0][0];
printf("determinant:%d\n", determinant);
return 0;
}2次正方行列の行列式を求めるプログラム
次に、2次正方行列の行列式を求めるプログラムは下記となります。
当然1次の時よりは難しいですが、まだまだ計算式は覚えやすいのではないでしょうか?
#include <stdio.h>
int main(void) {
/* 2次正方行列 */
int matA[2][2] = {
{1, 2},
{3, 4}
};
int determinant;
determinant = matA[0][0] * matA[1][1] - matA[0][1] * matA[1][0];
printf("determinant:%d\n", determinant);
return 0;
}3次正方行列の行列式を求めるプログラム
最後に3次正方行列の行列式を求めるプログラムを紹介していきます。
行列の成分の絶対値が大きいと桁あふれ(オーバーフロー)する場合があるので注意してください。
計算式にそのまま当てはめて計算する
ちょっと式は長くはなりますが、2次の時同様、3次の行列式の計算式にそのまま成分を当てはめて計算してやるのが一番無難だと思います。
#include <stdio.h>
int main(void) {
/* 3次正方行列 */
int matA[3][3] = {
{1, 2, 3},
{4, 2, 6},
{7, 8, 9}
};
int determinant;
determinant =
matA[0][0] * matA[1][1] * matA[2][2] +
matA[0][1] * matA[1][2] * matA[2][0] +
matA[0][2] * matA[1][0] * matA[2][1] -
matA[0][0] * matA[1][2] * matA[2][1] -
matA[0][1] * matA[1][0] * matA[2][2] -
matA[0][2] * matA[1][1] * matA[2][0];
printf("determinant:%d\n", determinant);
return 0;
}ループ処理を利用して計算する
上記のように直接計算式に当てはめて計算するのがどうしても嫌な場合は、下記のようなループで行列式を求めることも可能です。
#include <stdio.h>
int main(void) {
/* 3次正方行列 */
int matA[3][3] = {
{1, 2, 3},
{4, 2, 6},
{7, 8, 9}
};
int determinant;
int i;
int j0, j1, j2;
determinant = 0;
for (i = 0; i < 3; i++) {
j0 = i;
j1 = (j0 + 1) % 3;
j2 = (j0 + 2) % 3;
determinant += matA[0][j0] * matA[1][j1] * matA[2][j2];
}
for (i = 0; i < 3; i++) {
j0 = i;
j1 = (j0 - 1 + 3) % 3;
j2 = (j0 - 2 + 3) % 3;
determinant -= matA[0][j0] * matA[1][j1] * matA[2][j2];
}
printf("determinant:%d\n", determinant);
return 0;
}ちょっとだけソースコードがスッキリするかもしれないですが、剰余演算を求めたり、剰余演算結果が負の値にならないように制御したりする必要があるので、これはこれで実装がちょっと難しいです。
なので、私であれば行列式の計算式にそのまま成分を当てはめて計算しちゃいますねー。
もしかしたらもっといいループの書き方もあるかもしれませんが…。
スポンサーリンク
まとめ
このページでは、C言語での「行列式の求め方」について解説しました!
具体的には、下記の3つの正方行列に対する行列式の求め方について解説しました。
- 1次正方行列
- 2次正方行列
- 3次正方行列
1次正方行列の場合は行列式が自明ですし、2次と3次の場合は計算式をそのまま実装してやれば行列式を求めることができます。3次の行列式の場合は計算式が複雑なので、ちょっと注意が必要です。。
今回は3次以下の行列式の求め方についてのみ解説しましたが、4次以上の行列式も求めることは可能です。
「余因子展開を利用した行列の求め方」については下記ページで解説していますし、
 【C言語】余因子展開を利用した行列式の求め方
【C言語】余因子展開を利用した行列式の求め方
「行列の基本変形を利用した行列式の求め方」については下記ページで解説しています。
 【C言語】行列の基本変形を利用した行列式の求め方
【C言語】行列の基本変形を利用した行列式の求め方
これらのページを読んでいただければ、C言語で4次以上の行列式も求めることができるようになると思いますので、興味のある方はぜひ読んでみていただければと思います!