このページでは、C言語での「行列の基本変形を利用した行列式の求め方」について解説していきます。
下記のページで行列式の求め方を解説しましたが、ここで解説したのは3次以下の行列式の求め方のみでした。
 【C言語】3次以下の行列式の求め方
【C言語】3次以下の行列式の求め方
このページで紹介する「行列の基本変形」を利用すれば、4次以上の行列式も求めることができるようになります!しかも高速に!
この「行列の基本変形」は逆行列を求める際にも活用することができ、それについては下記ページで解説しています。このページの解説と重複する内容に関しては下記ページを参照する形で解説させていただいていますので、事前に目を通していただいた方が解説を理解しやすくなると思います。
 【C言語】掃き出し法による逆行列の求め方(4×4の逆行列も算出可能)
【C言語】掃き出し法による逆行列の求め方(4×4の逆行列も算出可能)
また、C言語での行列の扱い方については下記ページで解説していますので、そもそもC言語で行列を扱う方法をご存知ない方は、事前に下記ページを読んでいただくことをオススメします。
 【C言語】行列の扱い方
【C言語】行列の扱い方
Contents
行列の基本変形を利用した行列式の求め方
では、行列の基本変形を利用した行列式の求め方について解説していきます。
行列の基本変形
まず、行列の基本変形とは下記の6つの操作による行列の変形のことを言います。
- (1):2つの行を入れ替える
- (2):ある行を定数倍する(0倍以外)
- (3):ある行に他の行を定数倍したものを加える
- (4):2つの列を入れ替える
- (5):ある列を定数倍する(0倍以外)
- (6):ある列に他の列を定数倍したものを加える
操作(1)と操作(2)と操作(3)を「行基本変形」、操作(4)と操作(5)と操作(6)を「列基本変形」と呼びます。
このページで紹介するC言語プログラムにおいては、行基本変形のみを用います。
スポンサーリンク
行列の基本変形と行列式の関係
正方行列に対して先程紹介した行列の基本変形を行なった場合、行列式は下記のように変化します(変化しないものもありますが…)
- (1):2つの行を入れ替える
- 行列式:-1 倍される
- (2):ある行を定数倍する(0倍以外)
- 行列式:定数倍される
- (3):ある行に他の行を定数倍したものを加える
- 行列式:変わらない
- (4):2つの列を入れ替える
- 行列式:-1 倍される
- (5):ある列を定数倍する(0倍以外)
- 行列式:定数倍される
- (6):ある列に他の列を定数倍したものを加える
- 行列式:変わらない
操作(2)と操作(5)に関しては、「行や列に掛けた値」と同じ値が行列式に掛けられることになります。
行列の基本変形を利用した行列式の算出
各操作に対して行列式が上記のように変化していくことを考慮すれば、次のようにして求めたい正方行列の行列式を求めることができるようになります。
まず、求めたい正方行列の行列式を \(d\) とします。もちろん、この \(d\) の値はまだ不明です。

続いて、行列式を求めたい正方行列に対して行列の基本変形を行います。この時、基本変形を行なった際には、その操作に応じて行列式 \(d\) を変化させていきます。
例えば、ある行を \(c\) 倍するのであれば、行列式も \(cd\) に変化させます。
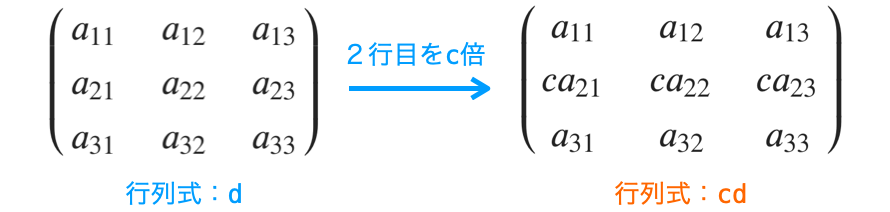
例えば、ある行と他の行を入れ替えるのであれば、行列式も \(-d\) に変化させます。

そして、こういった行列の基本変形を繰り返すことで「行列式が簡単に求められる行列」まで変形を行います。そこまでの行列の変形により、元々の正方行列の行列式 \(d\) が他の値に変化しているはずなので、この行列式を \(xd\) としたいと思います。
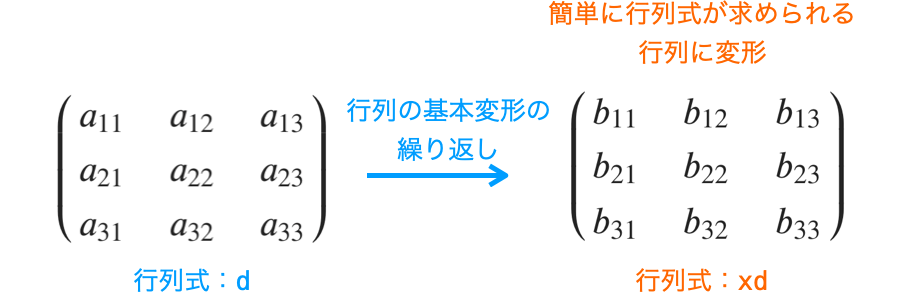
また、変形後の行列は「行列式が簡単に求められる行列」なので、行列式は簡単に求められるはずです。その行列式を \(y\) とします。

この時、あなたは「変形後の行列の行列式」として2つの値が得られたことになります。行列式 \(xd\) と行列式 \(y\) です。
そして、これらは両方とも「変形後の行列の行列式」なのですから、この2つは一致するはずです。つまり、\(xd\) = \(y\) が成立しますね!
なので、この等式を \(d\) について解けば、変形前の行列の行列式 \(d\) を求めることができます。この場合は \(d = y / x\) となります。

このように、正方行列を「簡単に行列式が求められる正方行列」にまで変形させれば、変形後の行列の行列式から変形前の正方行列(元々の正方行列)の行列式を逆算して求めることが可能です。
ただし、この逆算時には行列の基本変形によって行列式が変化した量が必要になります。
行列の基本変形では、行列式は下記のようにしか変化しないため、要は行列式が何倍されたかを覚えておけば良いことになります。
- \(-1\) 倍される
- 定数倍される
単位行列に変形して行列式を逆算
「簡単に行列式が求められる正方行列」の1つは単位行列となります。単位行列とは対角成分のみが \(1\) で、他の成分が \(0\) の正方行列です。
そして、この単位行列の行列式は次数に関わらず \(1\) となります。
したがって、行列の基本変形を利用した行列式の算出 で解説した通り、正方行列を行列の基本変形によって「単位行列」にまで変形することで、元々の正方行列の行列式を求めることができます。
例えば下記のような行列 \(A\) について考えると、
$$ A = \left ( \begin{array}{ccc} 0 & a_{12} & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right ) $$
まず、この行列 \(A\) の行列式を仮に \(d\) とし、さらに単位行列に変形するために操作(1)によって1行目と2行目を入れ替えます。これにより変形後の行列式は \(-d\) となります。

さらに、操作(2)によって2行目に \(1 / a_{12}\) を掛けます。これにより行列式は \(-d / a_{12}\) となります。

この時点で行列は単位行列に変形できたので、行列式は \(1\) になっているはずです。
つまり \(-d / a_{12} = 1\) が成立し、これを \(d\) に対して解けば \(d = -a_{12}\) であり、これが元々の行列 \(A\) の行列式となります。要は、単位行列を変形するまでに元々の行列式に「掛けた値」の逆数が求めるべき行列式となります。
ただし、正方行列によっては、行列の基本変形では単位行列に変形できない場合があります。変形できない場合は行列式は \(0\) となります。
スポンサーリンク
三角行列に変形して行列式を逆算
「簡単に行列式が求められる正方行列」としては三角行列(上三角行列と下三角行列)も挙げられます。
上三角行列とは、対角成分よりも下の成分が全て \(0\) となる正方行列であり、下三角行列とは対角成分よりも上の成分が全て \(0\) となる正方行列となります。
例えば下記の行列は上三角行列です。
$$ \left ( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array} \right ) $$
この上三角行列および下三角行列では、行列式が「対角成分全ての積」となります。
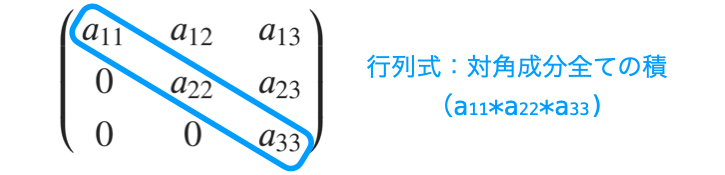
なので、行列の基本変形を利用した行列式の算出 で解説した通り、行列の基本変形によって正方行列を「上三角行列」or「下三角行列」に変形してやれば、三角行列の行列式から変形前の正方行列の行列式を求めることが可能です。
対角成分全ての積を計算する必要がある分、単位行列の時よりも処理が複雑そうにも感じますが、行列の基本変形による変形に関して言えば、単位行列に変形するよりも上三角行列 or 下三角行列に変形する方が簡単だと思います。
また、前述の通り、上三角行列 or 下三角行列では「対角成分全ての積」が行列式となります。したがって、対角成分に1つでも \(0\) が存在する場合、行列式は \(0\) となります。
単位行列への変形による行列式の算出の実装
続いて、行列の基本変形を利用した行列式の算出をC言語で実装していきたいと思います。
前述でも少し触れましたが、このページでは行列の基本変形の内、行基本変形のみ、すなわち下記における操作(1)・操作(2)・操作(3)のみを利用して実装していきます。
- (1):2つの行を入れ替える
- (2):ある行を定数倍する(0倍以外)
- (3):ある行に他の行を定数倍したものを加える
- (4):2つの列を入れ替える
- (5):ある列を定数倍する(0倍以外)
- (6):ある列に他の列を定数倍したものを加える
まずは、行基本変形により行列を単位行列に変形することで、行列式を算出していきたいと思います。
単位行列への変形は逆行列を求める時とほぼ同じ
ただ、行基本変形による単位行列への変形に関しては、下記の「逆行列の求め方」のページで詳しく解説していますので、このページでは解説は省略させていただきたいと思います。お手数ですが、必要に応じて下記ページを参照していただくようお願いいたします。
 【C言語】掃き出し法による逆行列の求め方(4×4の逆行列も算出可能)
【C言語】掃き出し法による逆行列の求め方(4×4の逆行列も算出可能)
基本的に上記ページで紹介している逆行列を求める時のプログラムと同様にして行列を変形していくことになるのですが、逆行列を求める時と行列式を求める時とでは次のような点が異なるので注意してください。
変形を行うのは正方行列に対してのみ
まず、逆行列を求める際は「逆行列を求めたい正方行列」の右側に「単位行列」を追加して拡張した行列に対して行基本変形を行いました。

その一方で、行列式を求める際には「行列式を求めたい正方行列」に対してのみ行基本変形を行うので問題ありません。
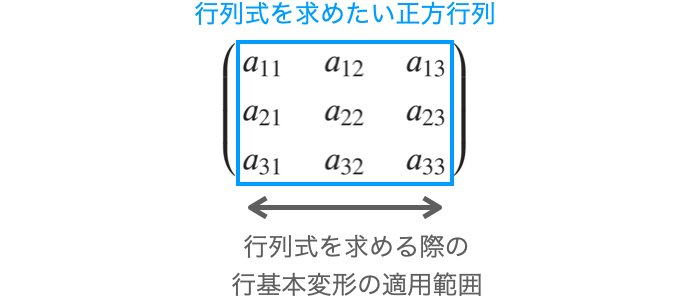
行列式に掛けた値を覚えておく必要あり
ただし、逆行列を求める際は行列式について意識しませんでしたが、行列式を求める際には、行基本変形を行うたびに行列式の変化量を計算していく必要があるので注意してください。
念の為、行基本変形における各操作を行なった際の行列式の変化を再掲しておきます。
- (1):2つの行を入れ替える
- 行列式:-1 倍される
- (2):ある行を定数倍する(0倍以外)
- 行列式:定数倍される
- (3):ある行に他の行を定数倍したものを加える
- 行列式:変わらない
単位行列変形後に行列式を算出
さらに、行列式を求める際には単位行列への変形ができれば処理が終了するというわけではなく、「変形後の行列の行列式」と「行基本変形による行列式の変化量」より、変形前の行列の行列式を算出する必要があります。
また、単位行列に変形できない場合は、行列式を 0 にする必要があります。
スポンサーリンク
単位行列への変形による行列式の算出プログラムの例
以上を踏まえると、単位行列への変形によって行列式を求めるプログラムのソースコードは下記のように記述することができます。
#include <stdio.h>
#include <math.h>
#define N 4 /* 逆行列を求める行列の行数・列数 */
#define MAX_ERR 1e-10 /* 許容する誤差 */
int main(void) {
/* 行列式を求める行列用の2次元配列 */
double mat[N][N];
/* matの行列式 */
double det;
/* 変形後の行列の行列式 */
double t_det;
/* 行基本変形で行列式に掛けられた値 */
double multiple;
/* 掃き出し法を行う行列 */
double sweep[N][N];
int i; /* 行 */
int j; /* 列 */
int k; /* 注目対角成分が存在する列 */
double a; /* 定数倍用 */
/* 行列の各成分を格納 */
mat[0][0] = 2; mat[0][1] = 1; mat[0][2] = 5; mat[0][3] = 3;
mat[1][0] = 3; mat[1][1] = 0; mat[1][2] = 1; mat[1][3] = 6;
mat[2][0] = 1; mat[2][1] = 4; mat[2][2] = 3; mat[2][3] = 3;
mat[3][0] = 8; mat[3][1] = 2; mat[3][2] = 0; mat[3][3] = 1;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
/* sweepの左側に行列式を求める行列をセット */
sweep[i][j] = mat[i][j];
}
}
multiple = 1;
/* 全ての列の対角成分に対する繰り返し */
for (k = 0; k < N; k++) {
/* 最大の絶対値を注目対角成分の絶対値と仮定 */
double max = fabs(sweep[k][k]);
int max_i = k;
/* k列目が最大の絶対値となる行を探す */
for (i = k + 1; i < N; i++) {
if (fabs(sweep[i][k]) > max) {
max = fabs(sweep[i][k]);
max_i = i;
}
}
if (fabs(sweep[max_i][k]) <= MAX_ERR) {
/* この場合単位行列に変形できない */
multiple = 0;
break;
}
/* 操作(1):k行目とmax_i行目を入れ替える */
if (k != max_i) {
for (j = 0; j < N; j++) {
double tmp = sweep[max_i][j];
sweep[max_i][j] = sweep[k][j];
sweep[k][j] = tmp;
}
/* 操作(1)により行列式が-1倍される */
multiple *= -1;
}
/* sweep[k][k]に掛けると1になる値を求める */
a = 1 / sweep[k][k];
/* 操作(2):k行目をa倍する */
for (j = 0; j < N; j++) {
/* これによりsweep[k][k]が1になる */
sweep[k][j] *= a;
}
/* 操作(2)により行列式がa倍される */
multiple *= a;
/* 操作(3)によりk行目以外の行のk列目を0にする */
for (i = 0; i < N; i++) {
if (i == k) {
/* k行目はそのまま */
continue;
}
/* k行目に掛ける値を求める */
a = -sweep[i][k];
for (j = 0; j < N; j++) {
/* i行目にk行目をa倍した行を足す */
/* これによりsweep[i][k]が0になる */
sweep[i][j] += sweep[k][j] * a;
}
}
}
if (multiple == 0) {
/* 単位行列に変形できなかった場合は行列式は0 */
det = 0;
} else {
/* 単位行列に変形できた場合 */
/* 変形後の行列は単位行列なので、変形後の行列の行列式の値は1 */
t_det = 1;
/* 元々のmatの行列式に掛けられた値で変形後の行列式を割る*/
det = t_det / multiple;
}
printf("%f\n", det);
return 0;
}実行すれば、正方行列 mat に格納されている成分に応じた行列式が表示されます。
-742.000000
さらに、下記で正方行列の次数(行数と列数)が設定できますので、こちらを変更すればもっと大きな次数の正方行列の行列式も求めることが可能です。
#define N 4 /* 行列式を求める行列の行数・列数 */また、特に k に対するループの中で、正方行列を行基本変形により単位行列に変形する処理に関しては、下記ページの 掃き出し法で逆行列を求めるプログラム例 とほぼ同じです(差分を取ってもらうと分かりやすいと思います)。
 【C言語】掃き出し法による逆行列の求め方(4×4の逆行列も算出可能)
【C言語】掃き出し法による逆行列の求め方(4×4の逆行列も算出可能)
ですので、k に対するループの中の処理内容等を知りたい方は上記ページを参照していただければと思います。
単位行列への変形による行列式算出の特徴
下記ページで行列式を余因子展開を利用して求める方法について解説しているのですが、行列式を求める速度に関しては、本ページで解説している行列の基本変形を利用した方法の方が断然速いです。
 【C言語】余因子展開を利用した行列式の求め方
【C言語】余因子展開を利用した行列式の求め方
例えば N = 12 の時だと、私の環境では余因子展開を利用した場合と行列の基本変形を利用した場合とでは、行列式を求める時間が下記のように大きく違いました。
- 余因子展開:15000 [ms] 程度
- 行列の基本変形:1 [ms] 未満
ただし、行列の基本変形を利用した方法においては、たとえ用意した正方行列の成分が全て整数であったとしても、求める行列式に誤差が発生する可能性があるので注意してください(小数点以下の値を扱う必要があるので浮動小数点数を利用する必要がある)。
余因子展開を利用した方法においては、行列式を求める際に逆数の計算や割り算を行う必要がないため、用意した正方行列の成分が「全て整数の場合」は誤差が発生しません(整数同士の演算のみで行列式を求められる)。
行列の基本変形を利用した方法においても、上手くやれば誤差が発生しないようにできるかもしれませんが…。とりあえず上記のプログラムでは誤差が発生する可能性があるので注意してください。
誤差に関して言えば、次に説明する三角行列への変形の方が、対角成分を 1 にするための演算が減る分、誤差も減らせると思います。
三角行列への変形による行列式の算出の実装
次は行基本変形により、行列を三角行列に変形することで行列式を算出していきます。
三角行列としては「上三角形行列」と「下三角行列」とが存在しますが、このページでは上三角行列への変形を行うことで行列式を算出します。
スポンサーリンク
三角行列への変形の仕方
行基本変形による行列の三角化は、単位行列への変形による行列式の算出の実装 で説明した単位行列への変形を少し変更するだけで実現することができます。
そのため、単位行列への変形による行列式の算出プログラムの例 で紹介したソースコードからの変更必要箇所に焦点を当てて解説していきたいと思います。
操作(2)は不要
単位行列への変形においては、対角成分を 1 にする必要があるため、それを実現するために操作(2)の「ある行を定数倍する(0倍以外)」が必要でした。
それに対し、上三角行列では対角成分が 1 である必要はないため、操作(2)を行う必要はありません。
したがって、三角行列への変形においては、単位行列への変形による行列式の算出プログラムの例 で紹介したソースコードにおける下記の操作(2)に関する処理は不要となります。
/* sweep[k][k]に掛けると1になる値を求める */
a = 1 / sweep[k][k];
/* 操作(2):k行目をa倍する */
for (j = 0; j < N; j++) {
/* これによりsweep[k][k]が1になる */
sweep[k][j] *= a;
}
/* 操作(2)により行列式がa倍される */
multiple *= a;操作(3)は注目している対角成分より下側のみに実施
また、単位行列への変形においては対角成分以外を全て 0 にする必要があるため、それを実現するために操作(3)の「ある行に他の行を定数倍したものを加える」を、対角成分が存在する行以外の “全ての行” に対して行う必要がありました。
それに対し、上三角行列では対角成分よりも上側の成分に関しては 0 にする必要がないため、操作(3)は対角成分が存在する行の “上側の行” に対しては行う必要はありません。操作(3)は対角成分が存在する行の “下側の行” のみに行うだけでも上三角行列への変形は実現できます。
さらに、操作(3)で定数倍する際に用いる倍数は、単位行列への変形においては 0 にしたい成分の符号を反転した値 でしたが、三角行列への変形においては 0 にしたい成分の符号を反転した値 / 注目している対角成分の値 とする必要があります。これは、操作(2)を行わなくなったため、注目している対角成分の値 が 1 でなくなったためです。
したがって、三角行列への変形においては、単位行列への変形による行列式の算出プログラムの例 で紹介したソースコードにおける下記の操作(3)に関する処理は、
/* 操作(3)によりk行目以外の行のk列目を0にする */
for (i = 0; i < N; i++) {
if (i == k) {
/* k行目はそのまま */
continue;
}
/* k行目に掛ける値を求める */
a = -sweep[i][k];
for (j = 0; j < N; j++) {
/* i行目にk行目をa倍した行を足す */
/* これによりsweep[i][k]が0になる */
sweep[i][j] += sweep[k][j] * a;
}
}下記のように変更する必要があります。
/* 操作(3)によりk行目よりも下の行のk列目を0にする */
for (i = k + 1; i < N; i++) {
/* k行目に掛ける値を求める */
a = -sweep[i][k] / sweep[k][k];
for (j = 0; j < N; j++) {
/* i行目にk行目をa倍した行を足す */
/* これによりsweep[i][k]が0になる */
sweep[i][j] += sweep[k][j] * a;
}
}三角行列の行列式は全対角成分の積
前述の通り、変形前の正方行列の行列式を求めるためには、変形後の正方行列の行列式が必要になります。
変形後の正方行列が単位行列の場合、行列式は必ず 1 になるので計算は不要でした。
その一方で、変形後の正方行列が三角行列の場合、行列式は「全対角成分の積」となりますので、この積を計算してやる必要があります。
したがって、単位行列への変形による行列式の算出プログラムの例 で紹介したソースコードにおける下記の変形後の正方行列の行列式を求める処理は、
/* 変形後の行列は単位行列なので、変形後の行列の行列式の値は1 */
t_det = 1;下記のように変更する必要があります。
/* 変形後の三角行列の行列式を求める */
t_det = 1;
for (k = 0; k < N; k++) {
/* 全ての対角成分の積を取る */
t_det *= sweep[k][k];
}三角行列への変形による行列式の算出プログラムの例
以上を踏まえると、三角行列への変形によって行列式を求めるプログラムのソースコードは下記のように記述することができます。
#include <stdio.h>
#include <math.h>
#define N 4 /* 行列式を求める行列の行数・列数 */
#define MAX_ERR 1e-10 /* 許容する誤差 */
int main(void) {
/* 行列式を求める行列用の2次元配列 */
double mat[N][N];
/* matの行列式 */
double det;
/* 変形後の行列の行列式 */
double t_det;
/* 行基本変形で行列式に掛けられた値 */
double multiple;
/* 掃き出し法を行う行列 */
double sweep[N][N];
int i; /* 行 */
int j; /* 列 */
int k; /* 注目対角成分が存在する列 */
double a; /* 定数倍用 */
/* 行列の各成分を格納 */
mat[0][0] = 2; mat[0][1] = 1; mat[0][2] = 5; mat[0][3] = 3;
mat[1][0] = 3; mat[1][1] = 0; mat[1][2] = 1; mat[1][3] = 6;
mat[2][0] = 1; mat[2][1] = 4; mat[2][2] = 3; mat[2][3] = 3;
mat[3][0] = 8; mat[3][1] = 2; mat[3][2] = 0; mat[3][3] = 1;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
/* sweepの左側に行列式を求める行列をセット */
sweep[i][j] = mat[i][j];
}
}
multiple = 1;
/* 全ての列の対角成分に対する繰り返し */
for (k = 0; k < N; k++) {
/* 最大の絶対値を注目対角成分の絶対値と仮定 */
double max = fabs(sweep[k][k]);
int max_i = k;
/* k列目が最大の絶対値となる行を探す */
for (i = k + 1; i < N; i++) {
if (fabs(sweep[i][k]) > max) {
max = fabs(sweep[i][k]);
max_i = i;
}
}
if (fabs(sweep[max_i][k]) <= MAX_ERR) {
/* この場合対角成分が0になる */
multiple = 0;
break;
}
/* 操作(1):k行目とmax_i行目を入れ替える */
if (k != max_i) {
for (j = 0; j < N; j++) {
double tmp = sweep[max_i][j];
sweep[max_i][j] = sweep[k][j];
sweep[k][j] = tmp;
}
/* 操作(1)により行列式が-1倍される */
multiple *= -1;
}
/* 操作(3)によりk行目よりも下の行のk列目を0にする */
for (i = k + 1; i < N; i++) {
/* k行目に掛ける値を求める */
a = -sweep[i][k] / sweep[k][k];
for (j = 0; j < N; j++) {
/* i行目にk行目をa倍した行を足す */
/* これによりsweep[i][k]が0になる */
sweep[i][j] += sweep[k][j] * a;
}
}
}
if (multiple == 0) {
/* 対角成分に1つでも0がある場合は行列式は0 */
det = 0;
} else {
/* 三角行列に変形できた場合 */
/* 変形後の三角行列の行列式を求める */
t_det = 1;
for (k = 0; k < N; k++) {
/* 全ての対角成分の積を取る */
t_det *= sweep[k][k];
}
/* 元々のmatの行列式に掛けられた値で変形後の行列式を割る*/
det = t_det / multiple;
}
printf("%f\n", det);
return 0;
}表示される結果や正方行列の次数の変更方法、注意点等に関しては 単位行列への変形による行列式の算出プログラムの例 と同様ですので、ここでの説明は省略させていただきます。
まとめ
このページでは、「行列の基本変形を利用した行列式の求め方」について解説しました!
正方行列を行列の基本変形により「行列式が簡単に求められる行列」に変形することで、変形後の行列の行列式からの逆算により簡単に変形前の行列式を求めることができます。
高速に行列式を求めることが可能ですが、行列式を求める正方行列の成分が全て整数である場合でも誤差が発生する可能性があるので注意してください。工夫次第で無くすこともできるのかもしれませんが、とりあえず単純に実装するだけだと誤差は発生する可能性があります。
おそらくそんなに気にならない程度の誤差だとは思いますが、特に誤差の原因となる浮動小数点数を使わずに行列式を求めたい場合は、下記ページの「余因子展開を利用した行列式の算出」の方がオススメです。
 【C言語】余因子展開を利用した行列式の求め方
【C言語】余因子展開を利用した行列式の求め方
余因子展開は再帰呼び出しの理解にも繋がりますので、まだ読んでいない方は是非読んでみてください!