平成27年度春期午後のアルゴリズム問題である問8の私の解き方・考え方について解説していきます。
問題
IPAの公式サイトで公開されています。このページでは問8についての解説を行います。
https://www.jitec.ipa.go.jp/1_04hanni_sukiru/mondai_kaitou_2015h27_2/2015h27a_fe_pm_qs.pdf
問題の概要
配列内からn番目に小さい数を探索するアルゴリズムに関する問題です。この問題では特にクイックソートを利用してその探索を行います。
スポンサーリンク
設問1
処理終了後のTopとLastの値が問われている問題です。これを解くには与えられた配列を用いて実際にプログラムがどう動いてTopとLastがどう変化していくかを追っていく必要があります。
[プログラム]の9〜24行目はこんな感じの動きになっています。各色枠の動きを頭に入れておきましょう。

それではSelect関数の動きを追っていきましょう。
まずSelect関数スタート時の配列x[ ]や変数i、変数jは下記のようになっています。Pivotはピンクで示した6です。
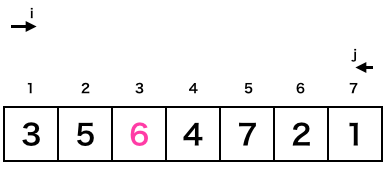
この状態からx[i]が6以上の値が見つかるまでiを右方向に移動させながら探索、x[i]が6以下の値が見つかるまでjを左方向に移動させながら探索を行います。
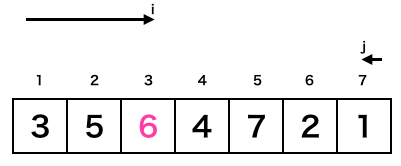
iに関してはx[3]が初めての6以下の数字であり、jに関してはx[7]が初めての6以下の数字となり、この時点のiとjで探索が終わります。ここまでが[プログラム]のオレンジ枠と緑枠の動きとなります。
続いてx[i]とx[j]の値の交換を行います。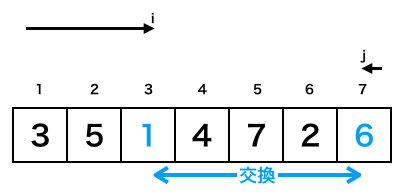
これが[プログラム]の赤枠の処理になります。さらにこの後にiを1増やし、jを1減らします。
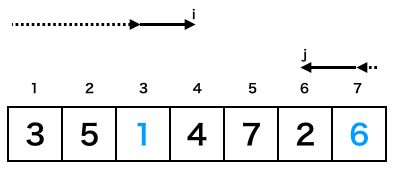
ここまでが[プログラム]の9〜24行目の処理の流れです。これをiがj以上になるまで続けられます。
[プログラム]の9〜24行目の2巡目の処理が完了すると下記のような状態になります。
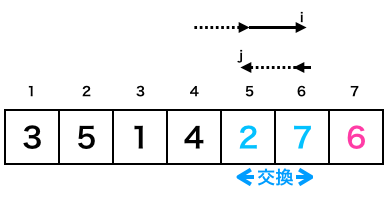
つまり、iが6、jが5となります。次のループではオレンジ枠・緑枠ともに一度もif文が成立しません。さらにこの時iがj以上となっていますので、[プログラム]の9〜24行目のループを17行目のbreakにより抜け出します。
ループを抜け出すと、[プログラム]の25〜30行目が実行され、TopとLastの値が更新されます。

i ≦ k は不成立、k ≦ j は成立ですので、Topは1のままとなり、Lastが5に更新されます。ですので[ a ]の答えは「Topに値1、Lastに値5」となります。
続いてはこの更新された配列x[ ]とTop、Lastに基づいてもう一度[プログラム]の9〜24行目のループ処理が実行されます。ループ開始時の状態は下記のような感じです。jはLastから始まるので探索範囲が狭まったことになります。
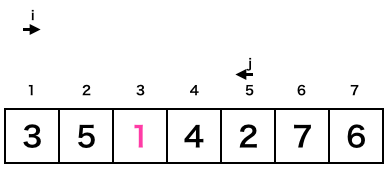
ループ1巡目が完了した時点だと各変数の様子は下記のようになります。
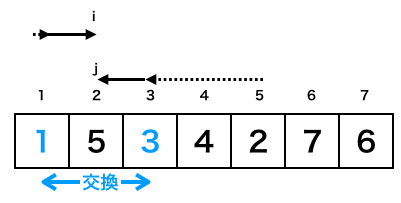
この時点でiもjも2となります。次のループ時にはオレンジ枠のif文は一度も成立しませんが、緑枠側はx[2]が1より大きいためjが1に更新されます。さらに、iがj以上になったので[プログラム]の9〜24行目のループを抜け、TopとLastの更新処理が実行されます。
今回はi ≦ k が成立、k ≦ j は不成立ですので、Lastは5のままとなり、Topが2に更新されます。ですので[ b ]の答えは「Topに値2、Lastに値5」となります。
設問2
設問2も与えられた配列を実際に入力した時の動きを追っていくしかないと思います。ただしプログラムの考え方は設問1と全く同じです。
γ部分が実行された後の結果をここで示します。設問1でプログラムの動きについては説明していますので、ここでは説明は割愛します。
・αの1回目
γの1回目終了後
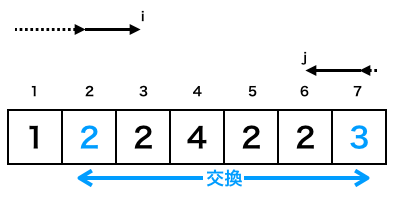
γの2回目終了後
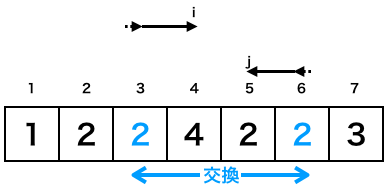
γの3回目終了後
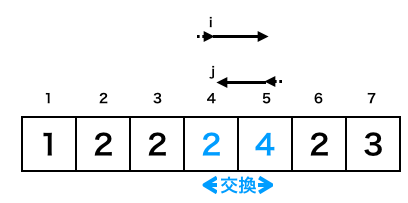
ここでiがj以上となるのでループ終了。Topは1、Lastは4に更新される。
・αの2回目
γの4回目終了後
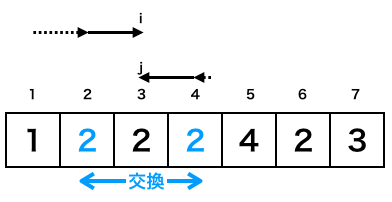
ここでiがj以上となるのでループ終了。Topは4、Lastは2に更新される。TopがLastを上回るのでSelect関数は終了。
以上より、αは2回、γは4回実行されます。ですので、[ c ]の答えは2、[ d ]の答えは4となります。
設問3
うーん、これも実際に配列入力した時の動きを見るのが良さそうですね。同じことばっかりやっていい加減疲れてきましたが・・・。
・「1,1,1,1,1,1」の場合
これは分かりやすいですね。[プログラム]の9〜24行目のオレンジ枠部分でx[i]がPivot以上かという判断が全て成立してしまうので配列外にまでアクセスしてしまいます。
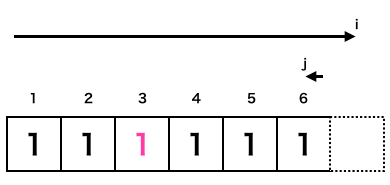
ですので[ e ]の答えは「配列の範囲を越えて参照する」となります。
・「1,3,2,4,2,2」の場合
こちらはγ後の各変数の状態がどう変更していくかを見ていってみましょう。
γの1回目終了後
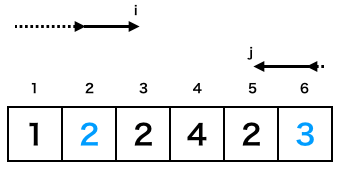
γの2回目終了後
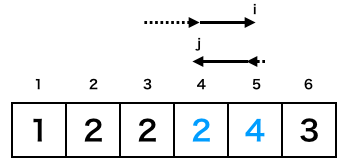
γの3回目終了後
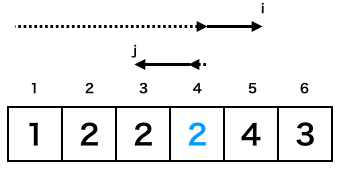
γの4回目終了後
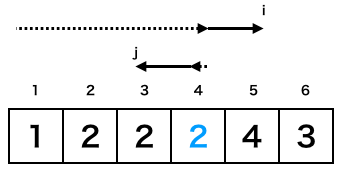
γ終了後の状態が3回目と4回目で全く同じですね。つまり5回目以降のγ終了後も同じ結果になると考えられ、ずっとTopがLastの値を上回らないので無限ループになってしまいます。
ですので[ f ]の答えは「処理が終了しない」となります。
スポンサーリンク
解いてみた感想
うーん、何度も同じことやらされたので疲れました。これぞアルゴリズム問題!といった感じなのでしょうか。
なぜこのアルゴリズムで数値の探索ができているかもわからなかったのですが、とにかくプログラムを実際に動かして考えてみることでなんとか正解を導くことができました。ただアルゴリズムの意味がよく分かってないので自信持った回答できないところが辛いところですね。それでもプログラムさえ追うことができれば解けてしまうのがアルゴリズム問題のいいところなのかもしれませんが。
★オススメページ★
下記ページから他の回の解説もたどれます。他の回のアルゴリズム問題の解き方がわからない場合は是非読んでみてください!
 基本情報技術者試験 午後問題「アルゴリズム」過去問の解き方 解説 まとめ
基本情報技術者試験 午後問題「アルゴリズム」過去問の解き方 解説 まとめ
本ページの図・プログラム・問題文について
図やプログラム、問題文はIPA公開の過去問題から引用しています。また図やプログラムに関しては説明に必要な部分に関してのみ加工して使用させていただいております。
出典:平成27年度 春期 基本情報技術者試験(FE)試験区分 午後 問8
アルゴリズム問題の対策(PR)
過去問を解いてみて感触はいかがだったでしょうか?
全く分からなかった...という方もいらっしゃるかもしれません。はっきりいってアルゴリズム問題は、特に慣れないと難易度は高いです。
なので、こういった方にはもっと "簡単なアルゴリズム問題を解いて慣れていく" ことをオススメします。で、この簡単なアルゴリズム問題を解くのにオススメの本が下記の うかる! 基本情報技術者 [午後・アルゴリズム編] です。
オススメする理由は、特に本の前半部分で難易度の低いアルゴリズムの紹介や解説が行われているところです。こういったアルゴリズムの動作などを実際にトレースして追ってみたりすることで簡単な問題からアルゴリズム問題に慣れていくことができます。
また、「アルゴリズムとは?」といったアルゴリズム入門から解説してくれているので、プログラミングをやったことない方にも親切な内容になっています。
アルゴリズム問題に全く手がつかないというような方は、まずは上記のような本でアルゴリズムに慣れるのがオススメです。
慣れてきたら、あとは実際の過去問を解いて "さらに考える力を養う" & "実際のアルゴリズム問題に慣れる" のが良いと思います。
私のサイトでも過去問の解説をしていますので是非参考にしてください。私の解説だけでなく、他の人の解説も参考にしたいような場合には、下記のような過去問の参考書もオススメです(アルゴリズム問題だけでなく、全問題の解説も充実しています)。






来年再度受験します。
情報セキュリティとアルゴリズムに特化する試験になるので、より対策が必要なのでつらいですががんばります。トレースやるとへとへとです
まきさん
コメントありがとうございます!
お久しぶりですね!
再受験、ぜひ頑張ってください!応援しています!
確かにトレースは大変ですが、それはおそらくみんな一緒、少なくとも私も一緒です。
逆に、へとへとになるのはしっかり考えられているという証拠だと思います!
ぜひ本番もへとへとになるまで考えてアルゴリズムを乗り越えましょう!
必ず合格つかみます
この大問(トレース問題)を一回やりました。
一度トレースをして再現をしてみたのですが、もう一回ゼロから再現をすることをしたほうがいいのでしょうか・・・(復習のために)
来年以降新試験もこういった問題が出るのか不透明ですが・・・・
今まで過去問はやってきましたが、アルゴリズム問題はあまり対策が出来てない状態で受験受けていたので(そんな状態で合格できるはずもない(笑))
奇跡的に38.25点とれたのがすごいと少しは自分を褒めます。
アルゴリズムは満点とるぞという意気込みでやります。((笑))
ちなみ令和元年の午前は72点でした。写真見て奮い立たせます
まきさん
コメントありがとうございます!
>一度トレースをして再現をしてみたのですが、もう一回ゼロから再現をすることをしたほうがいいのでしょうか・・・(復習のために)
復習するよりも、解いたことのない問題に挑戦するのが良いと思います!
新傾向になった場合にどうなるかはなんとも言えないのですが、
従来のアルゴリズム問題に関して言えば、アルゴリズム問題を解くためには
「問題をしっかり読んで理解する力」「問題をしっかり理解した上で論理的に考える力」
の2つが重要だと考えています。
この2つを身につけるためには、とにかく解いたことのないアルゴリズム問題を「自力で解けるまで解いてみる」ことが重要です。
「自力で解けるまで解いてみる」を何回も繰り返していけば、自然と上記の2つの力は身につくのではないかと思います。
そして、この2つの力があれば、(従来のアルゴリズム問題の場合であれば)本番にどんな問題が出題されたとしても対応できると思います。
(もちろん時間配分やケアレスミスを防ぐことも重要になりますが)
同じ問題を繰り返したとしても、その問題に慣れるだけで上記の力は身につかないと思います。
なので、出来れば同じ問題ではなく、解いたことのない問題に挑戦することをオススメします!
午前はバッチリのようですね!
ただ、油断して午前の点数が足りないと勿体無いので、出来れば直前でも良いので軽く復習しておくことをオススメします!
ありがとうございます。問題になれます
daeuさんこんばんは。
まきです。
10月末から演習問題という形で試験に出たアルゴリズムの問題にほぼ毎日取り組んでいます。時間はかかりますが慣れるまでの辛抱です。
基本事項がそもそも出来ていないので、動画等で試験で出題される基本的な考え方を身に着けてから試験問題に取り組んでます。
基本も身に着けていないのに試験問題を解くのは無謀ですから(笑)
情報セキュリティの問題も並行して行います。
ありがとうございました。
まきさん
コメントありがとうございます!
ほぼ毎日取り組んでいるのは素晴らしいと思います!
アルゴリズム問題は苦手意識があると本番で問題を読むことすら嫌になってしまいます…。
ですが、取り組む回数を増やしてやれば苦手意識も克服することができ、本番でも実力が発揮できるようにもなると思います!
試験までまだまだ日数はあると思いますので、根気強く取り組んでいきましょう!
応援してます!
daeuさん こんばんは。
まきです。
引き続き演習問題という形で試験に出たアルゴリズムの問題に
ほぼ毎日取り組んでいます。問題演習の中でこの分野が出る、
アルゴリズムの問題では頻出事項なんだと実感することだ出てきました。
以前は実感できませんでしたが、こんな形で出るかのと理解が深まっています。慣れることには出来ました。暗記することではなくて、なぜこの答なのかという理解が出来るようになればあとは少しづつ応用をしていくのかと、この27年も何回も行った結果、滞りなくトレースできるようになりました。
ありがとうございます。
情報セキュリティの問題も並行して行います。
ありがとうございました。
まきさん
コメントありがとうございます!
毎日勉強に取り組んでいるのはすごいですね!
>暗記することではなくて、なぜこの答なのかという理解が出来るようになればあとは少しづつ応用をしていくのかと
まさにその通りです!
アルゴリズム問題は暗記は不要で、問題文やプログラムから論理的に答えを導く問題です。
なぜ?と考え続けることで、その論理的に答えを導く力も身に付いていくと思います。
暗記問題は覚えていなければ解答を導くことができませんが、
アルゴリズム問題の場合は論理的に答えを導く力があれば、どんな問題でも解けると思います。
もちろん時間との戦いの側面もありますが、論理的に答えを導くことができれば安定して得点しやすい問題だと思います!
是非、今後も論理的に考えて答えを導くことに取り組んでいっていただければと思います。