画像の拡大縮小・リサイズの原理、アルゴリズムによる違いを解説！

このページでは画像の拡大縮小（リサイズ）がどのような原理で行われているかについて説明していきたいと思います。

画像とは画素の集まり

こちらの記事の最初の方でも説明しましたが、画像とは画素の集まりです。

画像データの構造・画素・ビットマップデータについて解説

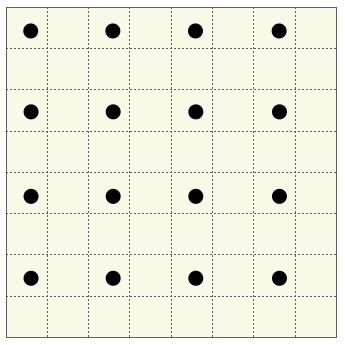
まずはRGBなどの輝度の話は置いといて、画素のみに注目して画像データを見てみると下図のようになります。

黒丸が画素を表しており、これは 4 x 4 の画像の例になります。マスは画素とは関係ないので注意してください。このマスは画素と画素の間の間隔を強調するためのものです。この画素と画素との間隔が、画像の拡大縮小を理解する上でのポイントになります。

画像の縮小

画像の縮小とは、この画素と画素の間隔を広げる処理と言えます。

ここでは画像を縦サイズと横サイズそれぞれ 0.5 倍に縮小する実例を用いて処理の流れを説明します。

画像を 0.5 倍にするためには、画素と画素の間隔を 2 倍（0.5の逆数）にします。

間隔を 2 倍にするので、最初にお見せした 4 x 4 の画像で考えると、黒丸の画素のみを残し白丸の画素は不要になります。

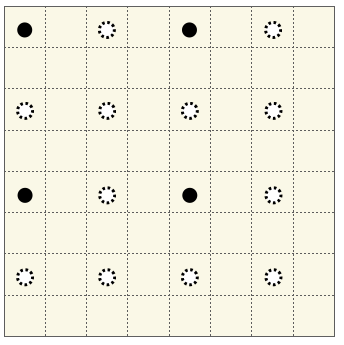
ちょうど 1 画素ずつ飛ばす感じになりましたね。

これにより画素数は縦横共に 1/2 になり、4 x 4 の画像が 2 x 2 の画像になったことになり、画像が縮小されたことになります。

このように画素を飛ばして不要な画素を削る処理を「間引き」処理と言ったりします。

0.5 倍にするにはこの間引き処理だけで処理完了です。

では次に 0.75 倍に縮小することを考えましょう。

0.75 倍の場合、画素と画素の間隔を 0.75 の逆数の 1.33… 倍にする処理となります。縮小後の画素の間隔は下図のようになります。

白色画素は削除され、代わりに「ピンク色の画素が必要になる」ところがポイントです。

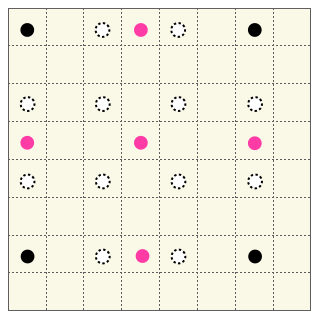
画素の間隔が 1.33（本当は 1.333333… だけど簡単のため 1.33 と書きます）になったので画像サイズは 0.75 倍されたことは理解できると思います。画素数は 3 x 3 になっています。

この縮小を行うにあたり、新たにピンクの画素を用意する必要がありました。この「もともと画像に存在しなかった位置の画素を用意すること」が画像拡大縮小の重要なポイントの１つになります。

もともとの画像に無かった位置の画素は周りの画素の輝度値から推測して求めてやる必要があります。

この周りの画素の輝度値から推測してもともと無かった画素を挿入する処理を補間と呼びます。

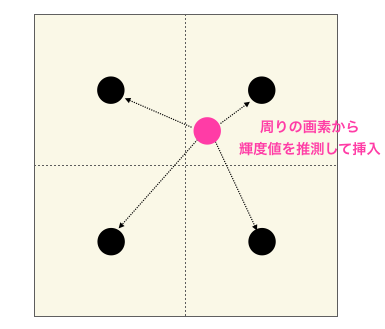
後述する画像の拡大においても、この補間が必要になります。つまり、画像の拡大縮小は単に画素と画素の間隔を変化させるだけでなく、保管を行う処理も必要になります。

また、この補間には様々なアルゴリズムが存在します。

このアルゴリズムの違いにより拡大縮小後の画質や処理速度に差が出ることになります。

私の Web サイトには比較的なシンプルなアルゴリズムである「最近傍補間法」と「線形補間法」を紹介していますのでこちらのページを読んで興味が湧いた人は拡大縮小処理を実装して見たい人は参考にしてください。

ここまでの話をまとめると、画像の縮小とは画素と画素の間隔を広げ、必要な画素を補間することです。

スポンサーリンク

画像の拡大

画像の拡大とは、縮小とは逆に画素と画素の間隔を狭める処理と言えます。

例えば画像を縦横それぞれを 2 倍に拡大する実例を用いて処理の流れを説明します。

画像を 2 倍に拡大するので、画素を追加して画素と画素の間隔を1/2にします。

最初にお見せした 4 x 4 の画像で考えると、下の図のように元々の画像に存在しなかった位置の画素（ピンク色の画素）を追加することで画素と画素の間隔を 1/2 にします。

上の図からも分かるように、拡大においても、元の画像にない位置の新たな画素が必要になります。

つまり、拡大においても縮小の時に説明した「補間」処理でこれらの画素を追加してやる必要があります。

ここまでの話をまとめると、画像の拡大処理とは画素と画素の間隔を狭め必要な画素を補間することと言えます。

拡大縮小前後の座標関係

ここまでは補間を中心に説明してきましたが、次は拡大縮小前後の画素の座標関係を説明していきたいと思います。

ここでは画像を縦方向に 2 倍、横方向にを 2 倍に拡大することを考えてみます。

これにより画素数は縦方向・横方向ともに 2 倍になります。例えば元画像が 2 x 2 のサイズであれば、拡大後の画像のサイズは 4 x 4 となります。

さらに、下の図のように、拡大後画像の色付きの画素は元画像の同じ色の画素の画素値と一致します。

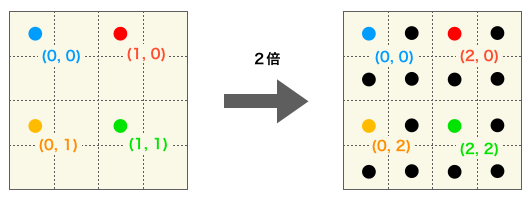
つまり、元画像の画素の座標を (x, y)、拡大後画像の画素の座標を (X, Y) とすれば、これらは下の式の関係にあると言えます。

x = 1 / 2 × X
y = 1 / 2 × Y

もうちょっと一般的に考えると、横方向に H 倍、縦方向に V 倍拡大する場合は、拡大後の座標 (X, Y) と元画像の座標 (x, y) の関係は下記式で表すことができます。

x = 1 / H × X
y = 1 / V × Y

上式を行列で表現すれば下記のように表すことも可能です。

$$ \left ( \begin{array}{c} x \\ y \end{array} \right ) = \left ( \begin{array}{cc} 1/H & 0 \\ 0 & 1/V \end{array} \right ) \left ( \begin{array}{c} X \\ Y \end{array} \right ) $$

つまり、画像の拡大前の座標は、行列と拡大後の座標の積で計算することが可能ということになります。

補間が必要になる画素

では、拡大後画像の他の座標の画素はどうなるでしょうか。

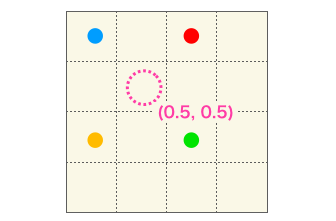
例えば下の図でピンク色の画素について考えてみます。

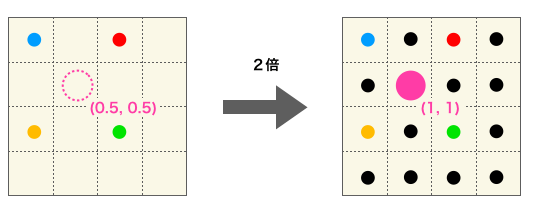
拡大後画像のピンク画素の座標は (1, 1) ですので、上の式に当てはめて考えると元画像上の対応する座標は (0.5, 0.5 )となります。

しかし、この座標は元画像上にはありません。

特にプログラムで扱うようなデジタルな画像には整数の座標しか存在しませんので、こういった小数点以下の座標の画素は存在しないのです。存在しない画素はどうすれば良いでしょうか？

ここで出てくるのが前に説明した補間です。

補間を行うことにより存在しない画素を追加して考えて処理を行うのです。

つまり、「拡大縮小後の画素値を求める際に必要な座標の画素」が元画像上に存在しない場合は補間処理を行う必要があります。

↑ の会話でも議論されているように、「拡大後の画素値を求める際に必要な座標の画素」が元画像上に存在するかどうかに関わらず、補間処理は拡大後の画素全てに対して行って良いです（アルゴリズムによって違いはあるかもしれませんが）。

もちろん「元画像上に存在するかどうかの判断」を行って補間処理を行う or 補間処理を行わないように処理を切り替えても良いですが、おそらく結果は変わらないと思いますし、その分プログラムが複雑になるというデメリットもあります。

スポンサーリンク

画像の拡大縮小処理まとめ

ここまでの流れをまとめておきます。

・縮小処理とは

画素と画素の間隔を広げ必要な画素を補間する

・拡大処理とは

画素と画素の間隔を狭め必要な画素を補間する

この二つの処理の違いは間隔を広げるか狭めるかの点だけであり、これらは間隔を何倍するかの違い（1より大きい数、1より小さい数）なので同じプログラムで実現可能です。

つまり、画像の拡大縮小処理とは画像中の画素と画素の間隔を変化させ足りない画素を補間する処理です。

下記の式で求まる（x, y）座標の画素が元画像上に存在しない場合、その画素が足りない画素となり補間が必須になります。

x = 1 / H × X
y = 1 / V × Y

補間アルゴリズムの例

画像の拡大縮小については少しずつイメージ湧いてきたでしょうか？

本サイトではC言語で画像の拡大縮小をプログラミングした時の解説やソースコードを載せたページも用意していますので、具体的な処理を見たい場合は是非参考にしていただければと思います。

最近傍補間（ニアレストネイバー）法を用いた拡大縮小

補間する画素に一番近い画素の輝度値を用いる方法です

C言語で画像の拡大縮小（最近傍補間編）

スポンサーリンク

線形補間法（バイリニア）を用いた拡大縮小

補間する画素の周りの画素の輝度値に基づいて輝度値を計算する方法です。

輝度値を補間画素からの距離に応じて周辺画素の輝度値を重み付けし、値を計算します。

C言語で画像の拡大縮小（線形補間編）

最近傍補間（ニアレストネイバー）と線形補間（バイリニア）の画質の違い

最後に補間のアルゴリズムによってどのような違いが出るかの紹介をしたいと思います（画像サイズが大きくてダウンロードに時間がかかる場合がありますのでご注意ください）。

写真などの自然画（縦横１０倍に拡大）

・入力画像

・最近傍補間による拡大結果

・線形補間による拡大結果

違いわかりますか？

最近傍だと観覧車の車輪あたりの線がギザギザしている感じがありますが、線形補間だと滑らかになっています。

さらに一部分を拡大してみるとその傾向がさらにわかりやすいと思います。どちらかというと線形補間の方が綺麗に見えると思います。

・最近傍補間による拡大結果（一部分拡大）

・線形補間による拡大結果（一部分拡大）

スポンサーリンク

パワポなどで作成したデジタル画（１０倍に拡大）

・入力画像

・最近傍補間による拡大結果

・線形補間による拡大結果

こちらも違いは自然画の時と同じです。

・最近傍補間による拡大結果

・線形補間による拡大結果

こちらはどちらかというと最近傍補間の方がきれいに見えると思います。

線形補間は周辺画素の平均を求めるような処理であり、若干ぼやけます。写真などの場合はそのぼやけにより綺麗に見えますが、パワポなどで作成したようなデジタルな絵では、線形補間だとぼやけるので最近傍補間の方が綺麗に見える人も多いと思います。

このように補間のアルゴリズムにより画質が異なります。自信が求める画質に合わせてアルゴリズムを選択しましょう。

まとめ

今回は拡大縮小がどのような処理であるかを解説しました。

要は拡大縮小というのは画素間の距離を変化させることです。

そしてその距離の変化を行うために必要になる追加の点を推測するのが補間になります。

かなりプログラミング寄りの考え方ですが、この２つを理解しておくと画像処理プログラミングがやりやすくなりますのでぜひ覚えて帰ってください！

このページでの解説は原理の話だったのでちょっと抽象度が高かったと思います。

下記ページでより具体的な拡大縮小時の補間の解説やプログラムの紹介を行っていますので、是非こちらも読んで拡大縮小の具体的なイメージをつかんでいただければと思います。

C言語で画像の拡大縮小（最近傍補間編）

C言語で画像の拡大縮小（線形補間編）