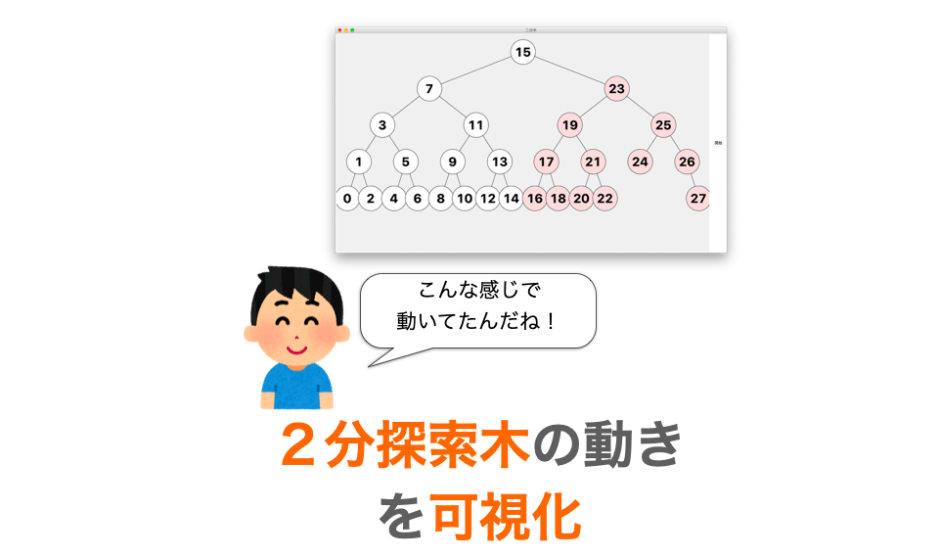
このページでは Python の Tkinter を用いて、平衡2分探索木(AVL 木)の動作を可視化していきたいと思います。
平衡2分探索木では、下記の関係を崩さないように木に対してノードの追加と削除が行われます。
- 左の子ノードの値 ≦ ノードの値 ≦ 右の子ノードの値
また、木の平衡状態(各ノードの左右の部分木の高さの差が1以下)を保つために、ノードの追加や削除が行われた後に回転が行われます。
このページでは、この平衡2分探索木に対してノードの追加・削除、さらに回転が行われた時に木がどのように変化していくかを可視化していきます。
出来上がりは下のアニメーションのようになります。

ノードを下記のように色付けすることで、どの操作が行われた時にどのノードが追加されたり位置が変化したりしているかを可視化しています。
- 緑:直前に追加したノード
- 赤:直前の左回転により移動したノード
- 青:直前の右回転により移動したノード
- 黄:直前の削除により移動したノード
このページでは可視化することを目的としていますので、2分探索木自体に関しての解説は省略しています。
下記の2つのページで「2分探索木」と「平衡2分探索木」の解説も行っていますので、2分探索木について理解したい方はこれらを参照していただければと思います。
 C言語で二分探索木(木構造・ツリー構造)をプログラミング
C言語で二分探索木(木構造・ツリー構造)をプログラミング
 【C言語】AVL 木(平衡2分探索木)の解説と実装
【C言語】AVL 木(平衡2分探索木)の解説と実装
スクリプトには2分探索木を構成するクラスも載せていますので、スクリプトを読んで、分からない点を上のページで補完していただくのが良いと思います。
Contents
平衡2分探索木の動作を可視化するスクリプト
平衡2分探索木に対してノードの追加・ノードの削除・回転が行われた時に木がどのように変化していくかを可視化するスクリプトは下記になります。
# -*- coding:utf-8 -*-
import tkinter
import time
import math
import random
# キャンバスのサイズ
CANVAS_WIDTH = 1200
CANVAS_HEIGHT = 700
# データの最大数
DATA_NUM = 127
# 描画時のウェイト(s)
WAIT = 0.1
# 円の半径
RADIUS = 30
class Node():
def __init__(self, number):
self.left = None
self.right = None
self.number = number
class Tree():
# 枝の方向を指す定数
LEFT = 0
RIGHT = 1
# 処理を表す定数
ADD = 0
LEFT_ROTATE = 1
RIGHT_ROTATE = 2
DELETE = 3
def __init__(self, view):
'木構造を制御するオブジェクト生成'
self.view = view
# 木の根をNoneに初期化
self.root = None
def add_node(self, number):
'ノードを追加'
# まだノードが一つもない場合
if not self.root:
# 根ノードとしてノードを追加
self.root = Node(number)
self.draw(Tree.ADD)
return True
# 根ノードから順に追加する場所を探索
node = self.root
# 根ノードからどう辿ったかを覚えておくリスト
branch = []
while True:
if number < node.number:
# 追加する値がノードの値よりも小さい場合
# 左の枝を辿ったことを覚えておく
branch.append(Tree.LEFT)
if not node.left:
# そのノードの左の子が無い場合(もう辿るべきノードが無い場合)*/
# その左の子の位置にノードを追加
node.left = Node(number)
# 追加完了したので処理終了
break
# 左の子がある場合は左の子を新たな注目ノードに設定
node = node.left
elif number > node.number:
# 追加する値がノードの値よりも大きい場合
# 右の枝を辿ったことを覚えておく
branch.append(Tree.RIGHT)
if not node.right:
# そのノードの右の子が無い場合(もう辿るべきノードが無い場合)
# その右の子の位置にノードを追加
node.right = Node(number)
# 追加完了したので処理終了
break
# 右の子がある場合は右の子を新たな注目ノードに設定
node = node.right
else:
# 追加する値とノードの値が同じ場合
print(str(number) + " already exist")
return False
# 一旦追加した状態で描画
self.draw(Tree.ADD)
# 平衡に保つための回転
self.balancing(self.root, None, None, branch)
return True
def delete_node(self, number):
'numberの値を持つノードを削除'
if not self.root:
return False
# 削除するノードを探索
node = self.root
# 親ノードはひとまずNone
parent = None
# 根ノードからどう辿ったかを覚えておくリスト
branch = []
while node:
if number < node.number:
# 探索する値よりもnodeの値が大きい場合
# 左の枝を辿ったことを覚えておく
branch.append(Tree.LEFT)
# 左の子ノードを辿る
parent = node
node = node.left
elif(number > node.number):
# 探索する値よりもnodeの値が小さい場合
# 右の枝を辿ったことを覚えておく
branch.append(Tree.RIGHT)
# 右の子ノードを辿る
parent = node
node = node.right
else:
# 見つかった場合
break
else:
# 見つからなかった場合
print(str(number) + "を持つノードはありません")
return False
if not node.left and not node.right:
# 子がいないノードの削除
self.delete_no_child_node(node, parent)
elif node.left and not node.right:
# 左の子のみいるノードの削除
self.delete_one_child_node(node, node.left)
elif not node.left and node.right:
# 右の子のみいるノードの削除
self.delete_one_child_node(node, node.right)
else:
# 左の子と右の子両方がいるノードの削除
self.delete_two_child_node(node, branch)
# キャンバスから削除したノードの情報を除去
self.remove(number)
# 除去後の木を描画
self.draw(Tree.DELETE)
# 平衡にするため回転
self.balancing(self.root, None, None, branch)
return True
def delete_no_child_node(self, node, parent):
'子のいないノード(node)を削除'
if parent:
# 親がいる場合
# nodeへの参照を外す
if parent.left == node:
parent.left = None
else:
parent.right = None
else:
# 親がいない場合
self.root = None
def delete_one_child_node(self, node, child):
'子が一方にだけいるノード(node)の削除'
# childeのデータをnodeにコピー
node.number = child.number
node.left = child.left
node.right = child.right
def delete_two_child_node(self, node, branch):
'子が2つあるノード(node)の削除'
# nodeの左の子孫ノードの中から最大値を持つノードを探索
max_node = node.left
max_parent = node
# 左の枝を辿ったことを覚えておく
branch.append(Tree.LEFT)
# 必ず右の子ノードの方が値が大きい
while max_node.right:
max_parent = max_node
max_node = max_node.right
# 右の枝を辿ったことを覚えておく
branch.append(Tree.RIGHT)
# 最大ノードのデータ(number)をnodeにコピー
node.number = max_node.number
# 最大ノード(max_node)を削除
# 最大ノードなので右の子ノードはいない前提
if not max_node.left:
# max_nodeに子がいない場合
self.delete_no_child_node(max_node, max_parent)
else:
# 子が1つある場合
self.delete_one_child_node(max_node, max_node.left)
def balancing(self, node, parent, direction, branch):
'各ノードの平衡係数を±1以下にする'
if not node:
return
if len(branch) > 0:
# 辿れる場合はまず目的のノードまで辿る
# 辿る子ノードを設定
if branch[0] == Tree.LEFT:
next = node.left
else:
next = node.right
# 子ノードを辿る
self.balancing(next, node, branch[0], branch[1:])
# 平衡係数を計算
left_height = self.get_height(node.left)
right_height = self.get_height(node.right)
balance = right_height - left_height
if balance > 1:
# 右の部分木が高くて並行状態でない場合
# 2重回転が必要かどうかを判断
if self.get_height(node.right.left) > self.get_height(node.right.right):
# 2重回転(Right Left Case)
self.right_left_rotate(node, parent, direction)
else:
# 1重回転(左回転)
self.left_rotate(node, parent, direction)
elif balance < -1:
# 左の部分木が高くて並行状態でない場合
# 2重回転が必要かどうかを判断
if self.get_height(node.left.right) > self.get_height(node.left.left):
# 2重回転(Left Right Case)
self.left_right_rotate(node, parent, direction)
else:
# 1重回転(右回転)
self.right_rotate(node, parent, direction)
def right_left_rotate(self, node, parent, direction):
'2重回転(Right Left Case)を行う'
print("right_left_rotate:" + str(node.number))
# nodeの右の子ノードを根として右回転
self.right_rotate(node.right, node, Tree.RIGHT)
# nodeを根として左回転
self.left_rotate(node, parent, direction)
def left_right_rotate(self, node, parent, direction):
'2重回転(Left Right Case)を行う'
print("left_right_rotate:" + str(node.number))
# nodeの左の子ノードを根として左回転
self.left_rotate(node.left, node, Tree.LEFT)
# nodeを根として右回転
self.right_rotate(node, parent, direction)
def left_rotate(self, node, parent, direction):
'nodeを根として左回転を行う'
print("left_rotate:" + str(node.number))
# 新しい根とするノードをpivotとして設定
pivot = node.right
# 左回転
if pivot:
node.right = pivot.left
pivot.left = node
# parentもしくはrootに新しい根ノードを参照させる
if not parent:
self.root = pivot
self.draw(Tree.LEFT_ROTATE)
return
# どちらの子に設定するかはdirectionから判断
if direction == Tree.LEFT:
parent.left = pivot
else:
parent.right = pivot
self.draw(Tree.LEFT_ROTATE)
def right_rotate(self, node, parent, direction):
'nodeを根として右回転を行う'
print("right_rotate:" + str(node.number))
# 新しい根とするノードをpivotとして設定
pivot = node.left
# 右回転
if pivot:
node.left = pivot.right
pivot.right = node
# parentもしくはrootに新しい根ノードを参照させる
if not parent:
self.root = pivot
self.draw(Tree.RIGHT_ROTATE)
return
# どちらの子に設定するかはdirectionから判断
if direction == Tree.LEFT:
parent.left = pivot
else:
parent.right = pivot
self.draw(Tree.RIGHT_ROTATE)
def get_height(self, node):
'nodeを根とした木の高さを取得する'
if not node:
# nodeが無いなら高さは0
return 0
# 左右の子を根とした木の高さを取得
left_height = self.get_height(node.left)
right_height = self.get_height(node.right)
# 大きい方に+1したものを木の高さとして返却
if left_height > right_height:
tree_height = left_height
else:
tree_height = right_height
return tree_height + 1
def draw(self, process):
'木の描画'
# rootを根とする木を描画
self.draw_node(self.root, [], process)
# キャンバスのアップデート依頼
self.view.update()
# スリープ
time.sleep(WAIT)
def draw_node(self, node, branch, process):
'枝を辿りながらnodeを根とする木を描画'
if not node:
return
# 処理によって円の色を変える
if process == Tree.LEFT_ROTATE:
diff_color = "#FFDDDD"
elif process == Tree.RIGHT_ROTATE:
diff_color = "#DDDDFF"
elif process == Tree.ADD:
diff_color = "#DDFFDD"
elif process == Tree.DELETE:
diff_color = "#FFFFDD"
# そのノードと親ノードを繋ぐ線を描画
self.view.draw_line(node, branch)
# そのノードを描画
self.view.draw_oval(node, branch, diff_color)
# そのノードの数字を描画
self.view.draw_text(node, branch)
# 左の子孫ノードを描画
branch.append(0)
self.draw_node(node.left, branch, process)
del branch[-1]
# 右の子孫ノードを描画
branch.append(1)
self.draw_node(node.right, branch, process)
del branch[-1]
def remove(self, number):
'numberをデータに持つノードの描画を除去'
self.view.remove_oval(number)
self.view.remove_line(number)
self.view.remove_text(number)
class View():
def __init__(self, master):
'UI関連のオブジェクト生成'
self.master = master
# 各種設定
self.drawn_oval = []
self.drawn_line = []
self.drawn_text = []
# キャンバスのサイズを決定
self.canvas_width = CANVAS_WIDTH
self.canvas_height = CANVAS_HEIGHT
# 情報表示用のフレームを作成
self.canvas_frame = tkinter.Frame(
master,
)
self.canvas_frame.grid(column=1, row=1)
# 操作用ウィジェットのフレームを作成
self.operation_frame = tkinter.Frame(
master,
)
self.operation_frame.grid(column=2, row=1, padx=10)
# キャンバスの生成と配置
self.canvas = tkinter.Canvas(
self.canvas_frame,
width=self.canvas_width,
height=self.canvas_height,
bg="#F0F0F0"
)
self.canvas.pack()
# 開始ボタンの生成と配置
self.button = tkinter.Button(
self.operation_frame,
text="開始",
)
self.button.pack()
def get_oval_coord(self, branch):
'キャンバス上の円の中心座標を取得'
# まずは木のどの位置の円を描画するかをbranchから計算
# branchの長さよりこのノードの縦方向の位置を計算
tree_y = len(branch)
# branchの要素より左から何番目のデータかを計算
tree_x = 0
i = 0
for n in branch[::-1]:
tree_x += n * 2 ** i
i += 1
# tree_xとtree_yをキャンバス上の座標に変換していく
# データ数より木の最大高さを計算
max_tree_height = math.ceil(math.log2(DATA_NUM + 0.5)) + 1
# マスの数を計算
num_horizontal = 2 ** (max_tree_height - 1) * 2
num_vertical = max_tree_height * 2
# 1マスの幅を計算(キャンバスの幅とマス数より)
one_width = self.canvas.winfo_width() / num_horizontal
# 1マスの高さを計算(キャンバスの高さとマス数より)
one_height = self.canvas.winfo_height() / num_vertical
# 円の中心座標を計算
x_space = num_horizontal / (2 ** tree_y * 2)
x = x_space * (tree_x * 2 + 1) * one_width
y = (tree_y * 2 + 1) * one_height
return x, y
def judge_same_coord(self, coord1, coord2):
'2つの座標が同じである角かを判断'
if not coord1 or not coord2:
# どちらか一方が None ならFalse
return False
if len(coord1) != len(coord2):
# 長さが違うならFalse
return False
# 座標が同じかを1つ1つチェック
for i in range(len(coord1)):
if not math.isclose(coord1[i], coord2[i]):
# 1つでも異なればFasle
return False
# 全部同じならTrue
return True
def draw_oval(self, node, branch, diff_color):
'ノードを表す円をdiff_color色で描画'
# 円の中心座標を取得
x, y = self.get_oval_coord(branch)
# 円の左上(x1, y1)と円の右下(x2, y2)を計算
coord = (
x - RADIUS,
y - RADIUS,
x + RADIUS,
y + RADIUS,
)
# タグを作成
tag = "oval_" + str(node.number)
# 前回描画時の円の座標を取得
bcoord = self.canvas.coords(tag)
# 前回と座標差分のあるノードだけ色を付ける
if self.judge_same_coord(coord, bcoord):
color = "#FFFFFF"
else:
color = diff_color
# 前回描画した円を削除
if tag in self.drawn_oval:
self.drawn_oval.remove(tag)
self.canvas.delete(tag)
# 円を新しく描画
self.canvas.create_oval(
coord[0], coord[1],
coord[2], coord[3],
fill=color,
tag=tag
)
# 描画した円のタグを覚えておく
self.drawn_oval.append(tag)
def draw_line(self, node, branch):
'ノードと親ノードを繋ぐ線を描画'
if len(branch) == 0:
# タグを作成
tag = "line_" + str(node.number)
# 前回描画時した線を削除
if tag in self.drawn_line:
self.drawn_line.remove(tag)
self.canvas.delete(tag)
# 親がないので線は描画しない
return
# ノードの中心座標取得
x, y = self.get_oval_coord(branch)
# 親ノードの中心座標取得
px, py = self.get_oval_coord(branch[:-1])
width = px - x
height = py - y
rad = math.atan2(height, width)
# タグを作成
tag = "line_" + str(node.number)
# 前回描画時した線を削除
if tag in self.drawn_line:
self.drawn_line.remove(tag)
self.canvas.delete(tag)
# 新しく線を描画
self.canvas.create_line(
x + RADIUS * math.cos(rad),
y + RADIUS * math.sin(rad),
px + RADIUS * math.cos(math.pi + rad),
py + RADIUS * math.sin(math.pi + rad),
tag=tag
)
# 描画した線のタグを覚えておく
self.drawn_line.append(tag)
def draw_text(self, node, branch):
'ノードの数字を描画'
# ノードの中心座標取得
x, y = self.get_oval_coord(branch)
# タグを作成
tag = "text_" + str(node.number)
# 前回描画時した数字を削除
if tag in self.drawn_text:
self.drawn_text.remove(tag)
self.canvas.delete(tag)
# 新しくテキストを描画
self.canvas.create_text(
x, y,
text=str(node.number),
tag=tag,
font=("", RADIUS, "bold")
)
# 描画したテキストのタグを覚えておく
self.drawn_text.append(tag)
def remove_oval(self, number):
'numberを持つノードの円を除去'
# タグを作成
tag = "oval_" + str(number)
# 前回描画時した線を削除
if tag in self.drawn_oval:
self.drawn_oval.remove(tag)
self.canvas.delete(tag)
def remove_line(self, number):
'numberを持つノードの線を除去'
# タグを作成
tag = "line_" + str(number)
# 前回描画時した線を削除
if tag in self.drawn_line:
self.drawn_line.remove(tag)
self.canvas.delete(tag)
def remove_text(self, number):
'numberを持つノードの数字を除去'
# タグを作成
tag = "text_" + str(number)
# 前回描画時した円を削除
if tag in self.drawn_text:
self.drawn_text.remove(tag)
self.canvas.delete(tag)
def update(self):
'キャンバスのアップデート'
self.canvas.update()
class Controller():
def __init__(self, view, tree):
'SortとViewを制御するオブジェクトを生成'
# 制御するViewとTreeのオブジェクト設定
self.view = view
self.tree = tree
self.num_list = []
# ボタンクリック時のイベントを受け付け
self.view.button["command"] = self.button_click
def button_click(self):
'ボタンクリック時の処理'
for i in range(DATA_NUM):
self.add(i)
for i in range(DATA_NUM):
self.delete(i)
def add(self, i):
'木へのノードの追加を行う'
num = random.randint(0, DATA_NUM)
# 木へのnumを持つノード追加
self.tree.add_node(num)
print("add:" + str(num))
def delete(self, i):
'木へのノードの削除を行う'
num = random.randint(0, DATA_NUM)
# 木からnumを持つノードを削除
self.tree.delete_node(num)
print("delete:" + str(num))
# アプリ生成
app = tkinter.Tk()
app.title("二分木")
# Viewオブジェクト生成
view = View(app)
# Treeオブジェクト生成
tree = Tree(view)
# Controllerオブジェクト生成
controller = Controller(view, tree)
# mainloopでイベント受付を待機
app.mainloop()スクリプトの実行
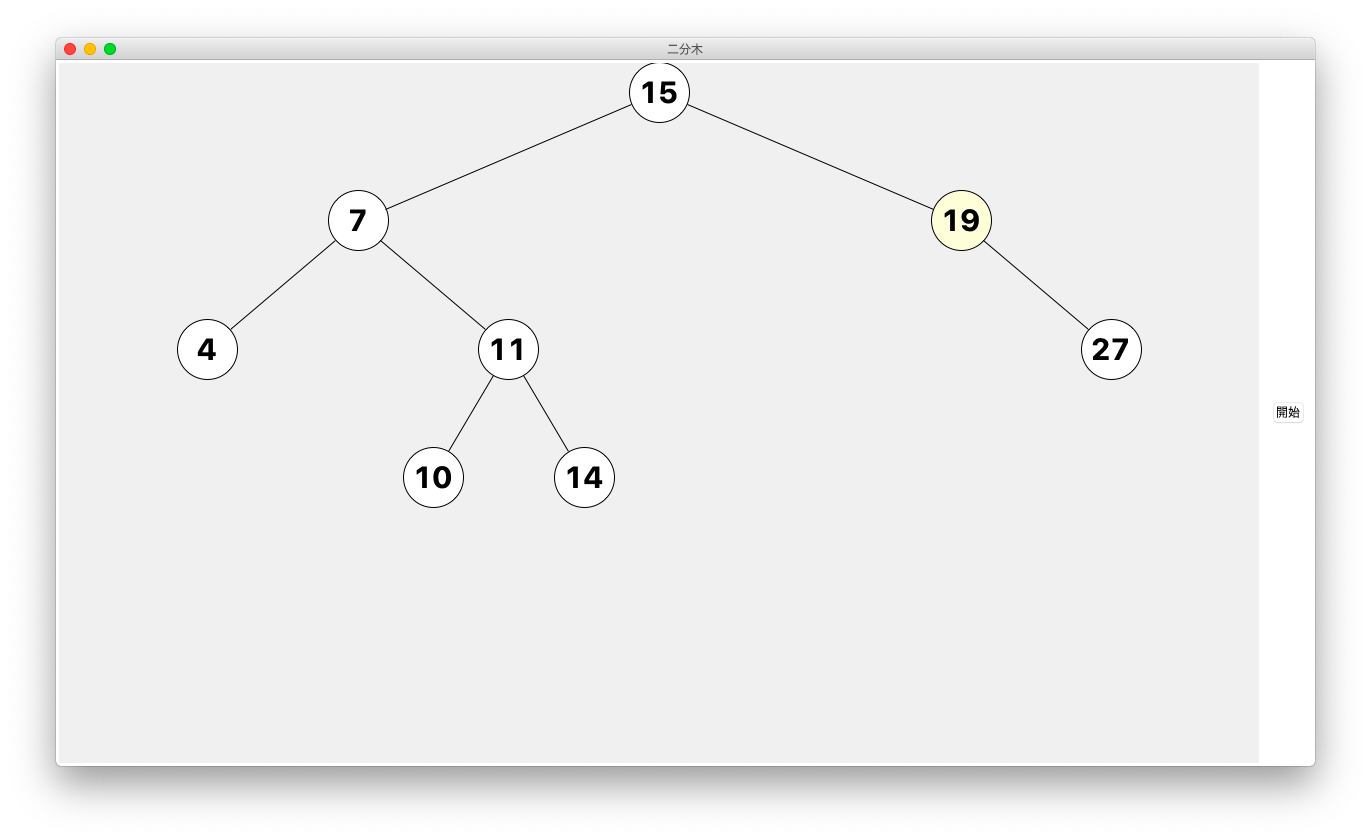
スクリプトを実行すると下のような画面が表示されます。
さらに「開始」ボタンをクリックすれば、木へのノードへの追加が行われていきます。
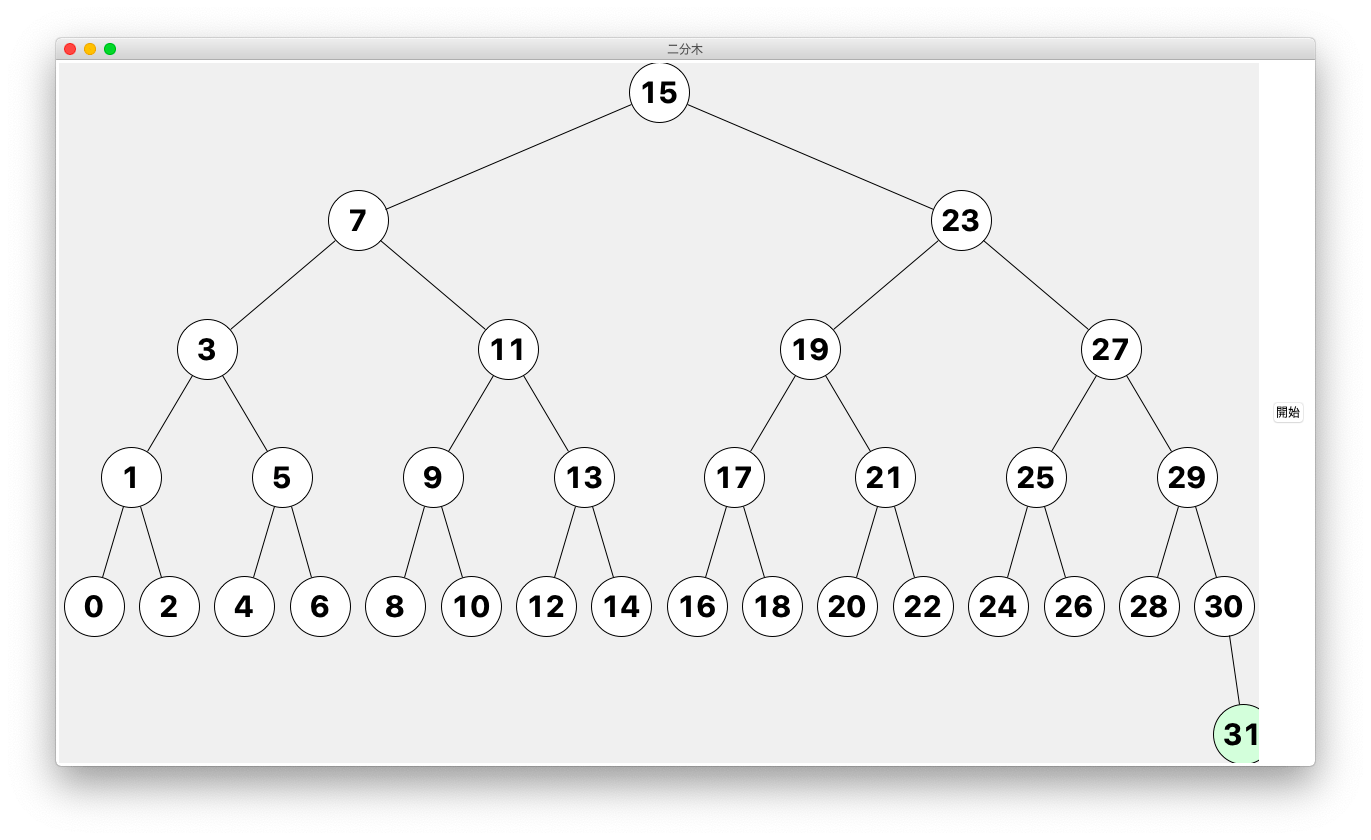
DATA_NUM 回分「0 〜 DATA_NUM - 1」までの数字がランダム選択され(DATA_NUM については次の節で解説)、その数字を持つノードが追加されていきます。
データの追加が終わると、今度はノードの削除が行われていきます。
DATA_NUM 回分「0 〜 DATA_NUM - 1」までの数字がランダム選択され(DATA_NUM については次の節で解説)、その数字を持つノードが削除されていきます。
前述の通り、各ノードは下記のように色付けを行なっています。
- 緑:直前に追加したノード
- 赤:直前の左回転により移動したノード
- 青:直前の右回転により移動したノード
- 黄:直前の削除により移動したノード
データの削除が終わると、アプリは停止します。
再度「開始」ボタンを押すと、その時の木の状態から再度ノードの追加と削除が行われます。
初期状態からまた実行したい場合は、アプリの再起動をしてください。
スポンサーリンク
スクリプトの設定
スクリプト先頭付近の下記を変更することで、簡単なスクリプトの設定を行うことができます。
# キャンバスのサイズ
CANVAS_WIDTH = 1200
CANVAS_HEIGHT = 700
# データの最大数
DATA_NUM = 127
# 描画時のウェイト(s)
WAIT = 0.1
# 円の半径
RADIUS = 30キャンバスのサイズ
CANVAS_WIDTH と CANVAS_HEIGHT を変更することで、キャンバスのサイズを変更可能です。
またキャンバスのサイズの変更に伴い、ノードとノードの間の距離も自動的に変化させるようにしています。
データの最大数
DATA_NUM を変更することでデータの最大数を変更可能です。
データの最大数に伴い、ノードの縦方向の間隔が変化します。
スポンサーリンク
描画時のウェイト
WAIT を変更することでキャンバスへの木の描画後のウェイト時間を変更することができます。時間は秒単位で指定します。
この時間を長くすることで、木の描画を行う間隔が長くなりますので、じっくり2分探索木の動作を観察したい方は WAIT を長くしてください。
円の半径
RADIUS を変更することでノードを表す円の半径を変更することができます。
またこの RADIUS の値に応じて、円の中に描画するノードのデータの値のフォントサイズも変化するようにしています。
スクリプトの解説
最後にスクリプトの解説を行います。
このスクリプトは下記の4つのクラスから構成されています。
ControllerクラスViewクラスNodeクラスTreeクラス
クラスごとに、どのような機能を提供するクラスかを解説していきます。
スポンサーリンク
Controller クラス
Controller クラスはユーザーからの操作を受け付け、その操作に応じて他のクラスに指示を行います。
このアプリでは、受け付けるユーザーからの操作は「開始ボタンのクリック」のみで、この操作を受け付けた時には bottun_click メソッドが実行されます。
開始ボタンクリック受付(button_click)
bottun_click メソッドでは add メソッドと delete メソッドをスクリプトの設定で紹介した DATA_NUM 回分実行しています。
さらに add メソッドと delete メソッドでは、後述する Tree メソッドの add_node メソッドと delete_node メソッドをそれぞれ実行し、ノードの追加とノードの削除を行っています。
この辺りを変更することで、追加するノードや削除するノードを変更することが可能です。
View クラス
View クラスはアプリの見た目の部分を制御するクラスになります。
特にこのアプリの目的は2分探索木の動きを可視化することですので、このアプリでは特に重要なクラスになります。
View クラスは下記の機能を提供します。
- 円の中心座標の取得(
get_oval_coord) - 円の描画(
draw_oval) - 線の描画(
draw_line) - 文字の描画(
draw_text) - 円の除去(
remove_oval) - 線の除去(
remove_line) - 文字の除去(
remove_text) - キャンバスの更新(
update) - 座標の一致の判断(
judge_same_coord)
円の中心座標の取得(get_oval_coord)
get_oval_coord メソッドは引数 branch で指定された位置の円の中心座標の計算を行って返却するメソッドになります。
この中心座標は下記のように2段階的に計算しています。
- 描画するノードが木のどの位置にあるかを決定
- 木の位置からキャンバス上の座標に変換
まずは「描画するノードが木のどの位置にあるかを決定」について解説します。
これには引数 branch を用います。
引数 branch は、木の根ノード〜描画するノードへの経路を格納したリストになります。
2分探索木における全てのノードは、根ノードから枝を辿ることで到達することができます。
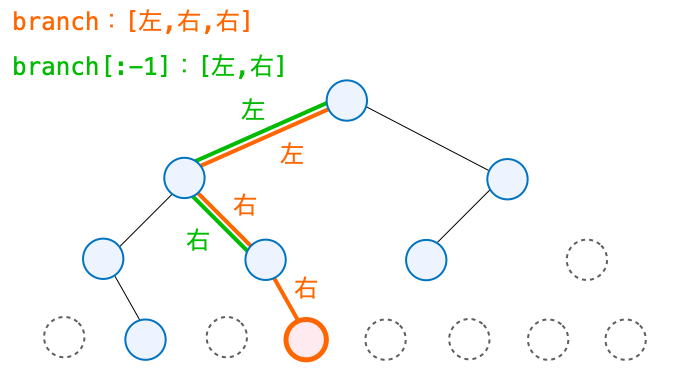
例えば下の図のオレンジのノードに辿るときは、根ノードから「左→右→右」と辿ることで到達することができます。
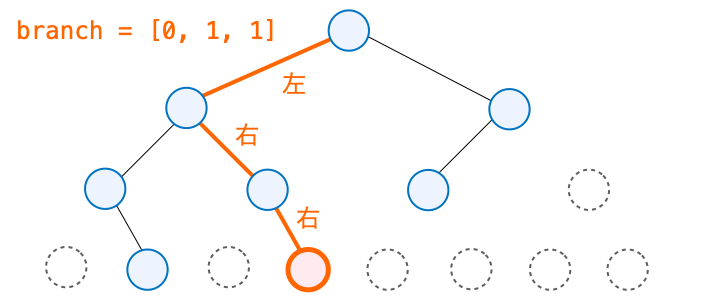
このとき、この経路を左の場合は “0“、右の場合は “1” として覚えておけば(上の図の branch)、この経路の情報からノードが木のどの位置に存在するかを決定することができます。
まず、ノードが根から何階層辿った位置にあるか(tree_y)は branch の要素数を調べることで決定することができます。
# branchの長さよりこのノードの縦方向の位置を計算
tree_y = len(branch)また、ノードがその階層において、左から何番目にあるか(tree_x)は branch の各要素の値より下記のように計算することができます(2進数を10真数に変換するイメージ)。
# branchの要素より左から何番目のデータかを計算
tree_x = 0
i = 0
for n in branch[::-1]:
tree_x += n * 2 ** i
i += 1上の図の例だと tree_x と tree_y 共に “3” になります。
こんな感じで描画するノード(円)が木のどの位置にあるかを事前に決定しておき、それから「木の位置からキャンバス上の座標に変換」することでキャンバス上に円を描画する位置を決定します。
続いて「木の位置からキャンバス上の座標に変換」することで円の中心座標の計算する方法について説明しておきます。
まず、円は下の図のようにキャンバスをマス目上に分割し、その上に描画することで、キャンバス内に指定した位置に描画できるように制御しています。
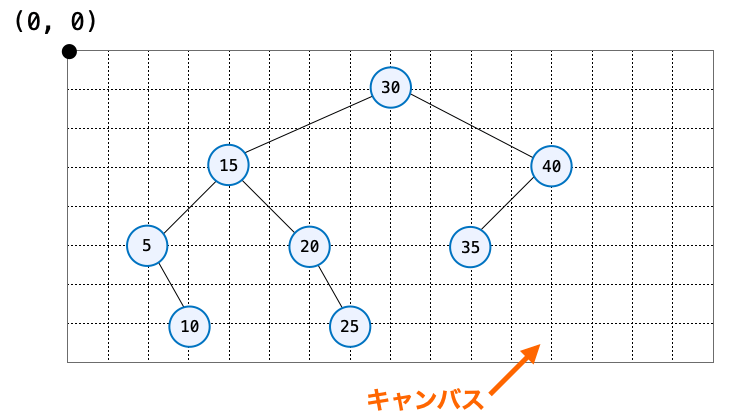
各円はくっつきすぎると見栄えが悪くなるので、必ず1マス以上空けて配置するようにしています。
この1マス以上開けて配置することを考え、後述する木の最大高さ(max_tree_height)を用いて、縦方向のマスの数と横方向のマスの数を下記により計算しています。
# マスの数を計算
num_horizontal = 2 ** (max_tree_height - 1) * 2
num_vertical = max_tree_height * 22 ** (max_tree_height - 1) は、2分探索木において木の一番深い階層に配置されるノードの最大数になります。
* 2 を行うことで、各円の間隔を1マス空けてもキャンバス内に円の中心座標が収まるようにマス数を設定することができます。
例えば木の最大高さ(max_tree_height)が “5” の場合はマスの数は下の図のように 32 x 10 になります。
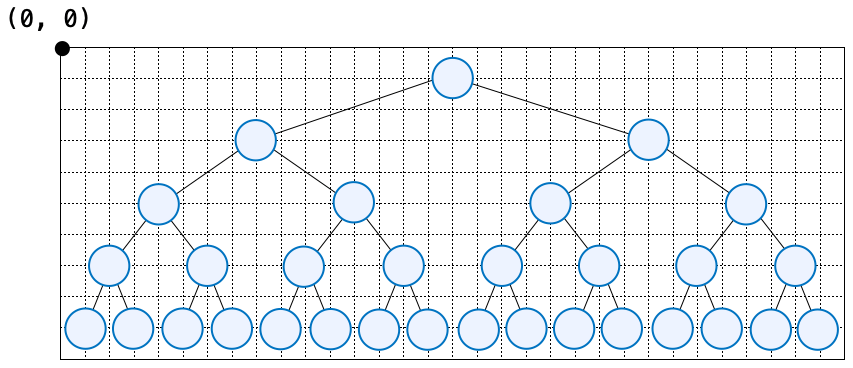
2分探索木の全枝にノードがある場合でも、各円の中心の間を1マス以上空けてもキャンバス内に収まることが確認できると思います(ただしマスのサイズよりも円のサイズが大きいと円同士は重なりますので注意してください)。
また前述した木の最大高さ(max_tree_height)はデータ数 DATA_NUM を用いて下記により計算しています。
# データ数より木の最大高さを計算
max_tree_height = math.ceil(math.log2(DATA_NUM + 0.5)) + 1ちょうど DATA_NUM が2の冪乗の値の場合に木の最大高さが増加するように + 0.5 を行っています
また今回は平衡2分探索木として AVL 木を用いており、左右の部分木の高さの差が ±1 発生することがあるため、円がはみ出すことを防ぐために + 1 しています
マス数が決まれば、各マスの幅(one_width)と高さ(one_height)が下記により計算できます。
# 1マスの幅を計算(キャンバスの幅とマス数より)
one_width = self.canvas.winfo_width() / num_horizontal
# 1マスの高さを計算(キャンバスの高さとマス数より)
one_height = self.canvas.winfo_height() / num_verticalマスの幅と高さ(one_width と one_height)が決まれば、tree_x と tree_y を用いて円の中心座標(x, y) を下記のように計算することができます。
# 円の中心座標を計算
x_space = num_horizontal / (2 ** tree_y * 2)
x = x_space * (tree_x * 2 + 1) * one_width
y = (tree_y * 2 + 1) * one_heighty に関しては tree_y の値に応じ、one_height の高さのマスの奇数番目のみに配置するように計算しています。
x に関してはちょっとややこしいので詳細を説明しておきます。
まず x_space は tree_y の階層の最大ノード数×2で横方向のマス数(num_horizontal)を割った値になります(tree_y の階層の最大ノード数は 2 ** tree_y で計算)。
木の最大高さが “5” の場合の tree_y=0、tree_y=2 の x_space は、それぞれ下図のピンク色の矢印、オレンジ色の矢印になります。
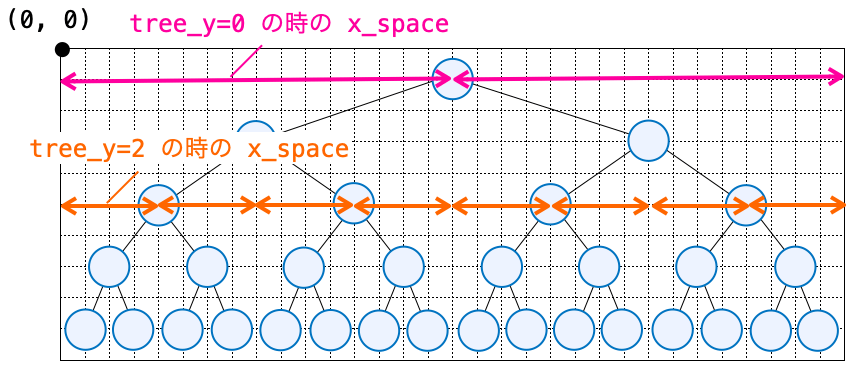
上図の特に tree_y=2 の x_space が分かりやすいと思いますが、この x_space の間隔の奇数番目にノードを配置すれば各ノードを等間隔に配置することができます。
そのため、最終的に下記のように、x_space の間隔の奇数番目の位置に x を配置するように計算を行っています(tree_x * 2 + 1 は必ず奇数になる)。
x = x_space * (tree_x * 2 + 1) * one_width円の描画(draw_oval)
draw_oval メソッドでは引数 branch により指定されたノードを表す円をキャンバスに描画します。
キャンバス上の円の中心座標を前述した get_oval_coord メソッドにより取得し、その中心座標(x, y)より下記のように円の左上と右下の座標を計算しています。
# 円の左上(x1, y1)と円の右下(x2, y2)を計算
coord = (
x - RADIUS,
y - RADIUS,
x + RADIUS,
y + RADIUS,
)さらに tkinter Canvas クラスの提供する create_oval メソッドを使用し、計算した座標(coord)に円の描画を行います。
# 円を新しく描画
self.canvas.create_oval(
coord[0], coord[1],
coord[2], coord[3],
fill=color,
tag=tag
)どのノードの円をキャンバスに描画しているかの管理は create_oval メソッドに指定した tag を View クラスの属性 drawn_obj リストに記録することで実現しています。
# 描画した円のタグを覚えておく
self.drawn_oval.append(tag)既に描画済みの円(直前のノードの追加・削除・回転時に描画した円)は、事前にキャンバスから除去した後に、円の描画(create_oval メソッドの実行)を行っています。
# 前回描画した円を削除
if tag in self.drawn_oval:
self.drawn_oval.remove(tag)
self.canvas.delete(tag)また、前回描画した時から円の位置が異なる場合は、引数 diff_color で指定された色で円の描画を行うようにしています(前回描画した時と円の位置が変わらない場合は白色で描画)。
# 前回描画時の円の座標を取得
bcoord = self.canvas.coords(tag)
# 前回と座標差分のあるノードだけ色を付ける
if self.judge_same_coord(coord, bcoord):
color = "#FFFFFF"
else:
color = diff_color前回描画した円の位置は tkinter Canvas クラスの提供する coord メソッドを実行することで取得しています(引数には描画時に指定した tag を指定)。
draw_oval メソッド実行時に、木に対する処理(ノードの追加・削除・回転)に応じて diff_color を指定することで、木に対する処理によって位置が変化したノードを色で見分けるようにすることができます。
線の描画(draw_line)
draw_line メソッドでは、引数 branch により指定されたノードを表す円と、そのノードの親ノードを表す円とを結ぶ線をキャンバスに描画します。
基本的な流れは draw_oval と同様ですので差分だけ解説していきます。
まず draw_line メソッドでは指定されたノードとその親ノードを結ぶ線を描画するので、親ノードを表す円の中心座標も必要になります。
親ノードを表す円の中心座標は get_oval_coord メソッドに branch[:-1] を引数として渡すことで取得することができます(branch[:-1] は branch から「親ノードから指定されたノードまでの経路」を除去したものになる)。
また単純に2つの円の中心座標を線で結ぶと、線が円内にも描画されて見栄えが悪いので、下図のように、円上の座標を計算しこの円上の座標を用いて線を描画するようにしています(y 軸が数学で学んだ方向と逆方向になっているので注意してください)。
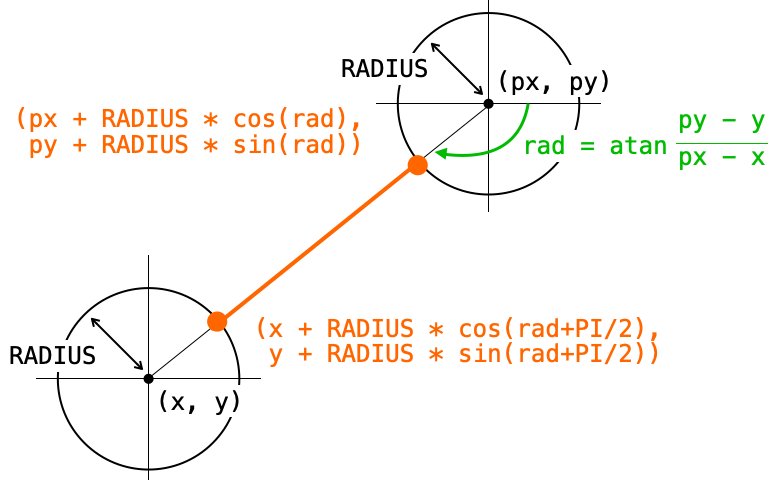
最終的に下記のように tkinter Canvas クラスの提供する create_line メソッドを使用し、2つの円上の座標を結ぶ線の描画行います。
# 新しく線を描画
self.canvas.create_line(
x + RADIUS * math.cos(rad),
y + RADIUS * math.sin(rad),
px + RADIUS * math.cos(math.pi + rad),
py + RADIUS * math.sin(math.pi + rad),
tag=tag
)また、親ノードがない場合(つまり根ノードの場合)は線を描画する必要がないので、メソッドの先頭部分で処理を終了するようにしています。
# 新しくテキストを描画
self.canvas.create_text(
x, y,
text=str(node.number),
tag=tag,
font=("", RADIUS, "bold")
)文字の描画(draw_text)
draw_text メソッドでは、引数 branch により指定されたノードを表す円の中心に、そのノードの持つデータ(数字)を描画します。
基本的な流れは draw_oval と同様です。
データの描画には、下記のように tkinter Canvas クラスの提供する create_text メソッドを使用します。
# 新しく線を描画
self.canvas.create_line(
x + RADIUS * math.cos(rad),
y + RADIUS * math.sin(rad),
px + RADIUS * math.cos(math.pi + rad),
py + RADIUS * math.sin(math.pi + rad),
tag=tag
)引数 font にはフォント情報を表すタプルを指定し、このタプルの第1要素にはフォントサイズを指定します。
このフォントサイズを RADIUS とすることで、円の半径に合わせてフォントサイズも変化するようにしています。
円の除去(remove_oval)
remove_oval では描画済みの円をキャンバス上から除去します。
指定されたデータに基づいて tag を作成し、キャンバス描画時(create_oval 実行時)にその tag が指定された円を tkinter Canvas クラスの delete メソッドを利用してキャンバスから除去します。
# 前回描画時した線を削除
if tag in self.drawn_oval:
self.drawn_oval.remove(tag)
self.canvas.delete(tag)どの tag に対応した円が描画済みかは drawn_oval リストでも管理していますので、このリストからもその tag を remove メソッドにより除去しています。
線の除去(remove_line)・文字の除去(remove_text)
remove_line と remove_text では、それぞれ描画済みの線とデータをキャンバス上から除去します。
remove_oval 同様の処理ですので説明は省略します。
キャンバスの更新(update)
update メソッドでは、それまでに描画や除去した結果を直ちにキャンバス上に反映します。
tkinter Canvas クラスの update メソッドを実行することで実現しています(このメソッドは単なる Canvas クラスの update メソッドのラッパー)。
座標の一致の判断(judge_same_coord)
judge_same_coord メソッドでは引数で指定された2つの座標データの比較を行い、同じ場合は True を、異なる場合は False を返却します。
指定された座標データが浮動小数点でも対応できるように math モジュールの isClose を利用しています。
if not math.isclose(coord1[i], coord2[i]):
# 1つでも異なればFasle
return False浮動小数点の場合、単に == や != では比較が上手くいかないので注意が必要です。
Node クラス
Node はノードそのものを表すクラスです。メソッドは持たず、単に属性のみを持つクラスになります。
self.left = None
self.right = None
self.number = numberleft と right は子ノードを参照する属性です。left と right がどんどん他のノードが繋がって木構造を形成します。
本当は left と right に対するノードの参照のセットや number の取得を行うメソッド等も用意したほうが良いのかもしれませんが、今回は他のクラスに直接 left と right の参照のセットも行わせています。
スポンサーリンク
Tree クラス
Tree クラスは平衡2分探索木を構成するために必要な機能を備えたクラスになります。
前述の通り、2分探索木と平衡2分探索木(AVL 木)については下記で解説していますので、2分探索木自体について知りたい方はこちらを参照していただければと思います。
 C言語で二分探索木(木構造・ツリー構造)をプログラミング
C言語で二分探索木(木構造・ツリー構造)をプログラミング
 【C言語】AVL 木(平衡2分探索木)の解説と実装
【C言語】AVL 木(平衡2分探索木)の解説と実装
また、このページで紹介している Python スクリプトの Tree クラスもコメントを充実させているつもりですので、スクリプトのコメントも併せて読んでいただければと思います。
ここでは特に可視化を行うための処理を行っている下記の2つについて解説したいと思います。
- 木の描画(
draw) - ノードの描画(
draw_node) - ノードの除去(
remove)
木の描画(draw)
Tree クラスの draw は木の描画を行うメソッドです。
と言っても、次に説明する draw_node メソッドの実行と、View クラスの update メソッドの実行をするだけです。
この draw メソッドはノードの追加(add_node)やノードの削除(delete_node)、回転(left_rotate・right_roate)で木のノードが変化した際に実行するようにしています。
ノードの描画(draw_node)
Tree クラスの draw_node はノードの描画を行うメソッドです。
引数 node で指定されたノード以下(そのノードと子孫ノード)の描画を行います。
また木に対する処理(ノードの追加や削除など)によって位置が変化したノードに他のノードと異なる色を設定することで、どの処理が行われ流ことで、どの部分のノードが変化したかがわかるようにしています。
具体的には引数 process に応じて下記のように異なる色を設定するようにしています。
# 処理によって円の色を変える
if process == Tree.LEFT_ROTATE:
diff_color = "#FFDDDD"
elif process == Tree.RIGHT_ROTATE:
diff_color = "#DDDDFF"
elif process == Tree.ADD:
diff_color = "#DDFFDD"
elif process == Tree.DELETE:
diff_color = "#FFFFDD"例えばノード追加後に木を描画する際は、draw メソッドの引数に Tree.RIGHT_ROTATE を指定してやれば、draw メソッドから呼び出されるこの draw_node メソッドで上記により、ノードの色として "#DDDDFF" が選択されるようになります。
さらに draw クラスの draw_circle・draw_line・draw_text を実行して円と線とデータの描画を行います。
最後に draw_node を再帰呼び出し(描画するノードには node.left と node.right を指定)することで node の子孫ノードの描画を行っています。
描画するノードが木のどの位置のものであるかを示すために、再帰呼び出し前に branch に要素を追加している点に注意してください。
ノードの除去(remove)
Tree クラスの remove はノードに関する描画を除去するメソッドです。
具体的には View クラスの remove_oval・remove_line・remove_text を実行して、引数 number で指定されたデータを持つノードを表す円や線、データのテキストの除去を行います。
まとめ
このページでは2分探索木の動きを可視化する方法について解説しました。
スクリプトの紹介もしていますが、特に Tree クラス以外をコピペし、Tree クラスは自作してみるのがおすすめの使い方です。
2分探索木というデータ構造はプログラミングするのはちょっと難し目だと思います(特に平衡状態を維持する AVL 木のプログラミングは難易度が回です)。
しかし、このページで紹介したスクリプトを利用して2分探索木の動きを可視化してやることで、2分探索木の動きを直感的に理解したり、プログラミングが誤っている場合でも何がおかしいのかを見つけやすくなります。
何より自身の作成したプログラムやスクリプトの動きを可視化してやることで、出来上がったときの喜びも倍増します。
是非みなさんもいろんなプログラムやスクリプトの動きの可視化に挑戦していただければと思います!
今回紹介したスクリプトのように、ボタンや図形の描画を行う GUI アプリを作成するには tkinter がオススメです。
おすすめの書籍(PR)
この tkinter の使い方を習得するための参考書としてはPythonでつくる ゲーム開発 入門講座がオススメです。
この本では主に tkinter を使用したゲームの開発を学べる参考書です。当然 tkinter について学べますし、題材がゲームなので楽しく学ぶ事もできます。
私も Python を始めた時はこの参考書で勉強しました!
ゲームだけでなく、いろんな GUI アプリを作成したい方にもオススメです!