特にアフィン変換・回転などの座標変換系の画像処理を行うためには「逆行列」の存在が非常に重要です。
このページでは、画像処理プログラミングにおいて「逆行列が重要である理由」を解説していきます。
例えばですが、回転を行うプログラムを下記で紹介しています。
 C言語で画像を回転
C言語で画像を回転
このプログラムで注目していただきたいのはループを「回転後」の座標に対して実施している点です。
回転後座標でループを行うということは、回転後座標が与えられており、そこから回転前座標を計算する必要があります。
これを行うためには、有名な回転行列をそのまま使用するのではなく、わざわざ逆行列を用いて計算を行う必要があります。
また下記ページで紹介しているスキューにおいても同様に、スキュー後の座標でのループを行っています。
そして、そのために、わざわざ逆行列を用いてスキュー処理を行っています。
 C言語で画像のスキュー
C言語で画像のスキュー
逆に変換前座標のループであれば、もっとシンプルな行列の演算で済むのに、なぜわざわざ逆行列を求めているのでしょうか。
これには明確な理由があります。それは画質の低下を防ぐためです。
Contents
画像の回転で違いを確認
まずは回転を例に、下記の2つの場合でプログラムの実行結果の画像にどのような違いがあるかを比較していきたいと思います。
- “回転前” 座標でのループの中で画像を回転するプログラム
- この場合、ループの中で回転行列をそのまま用いて回転後座標の計算を行う
- “回転後” 座標でのループの中で画像を回転するプログラム
- この場合、ループの中で回転行列の「逆行列」を用いて回転前座標の計算を行う
プログラムの大まかな説明は画像の回転のページをご参照ください。
 C言語で画像を回転
C言語で画像を回転
下記2つのプログラムの違いは回転処理を行っているループの箇所のみです。
座標に関して説明しておくと、変数 originalm と originaln は元画像上の横方向の座標および縦方向の座標となります(行列の演算式における x と y)。
また、m と n は回転後画像上の横方向の座標および縦方向の座標となります(行列の演算式における x' と y')。
さらに、行列演算で求めた結果の座標は実数となるため、その実数を四捨五入して整数化した結果が m0 と n0 となります。
ちなみに、JPEG 画像ファイルを読み込んで回転を行うプログラムとなっており、JPEG 画像ファイルを処理するための関数については下記ページで紹介しているものを利用していますのでご注意ください。また、これらの関数を利用するためには libjpeg をインストールする必要があるので、この点もご注意ください。
 【C言語】libjpegのインストールと使用方法・使用例
【C言語】libjpegのインストールと使用方法・使用例
回転行列をそのまま用いて回転
まずは、回転行列をそのまま用いて回転するプログラムのソースコードを紹介します。
この場合、回転前の座標に対するループの中で、下記の回転行列をそのまま用いて回転後座標を求めながら回転処理を行うことになります。
$$ \left ( \begin{array}{c} x’ \\ y’ \end{array} \right ) = \left ( \begin{array}{cc} \cos \theta & – \sin \theta \\ \sin \theta & \cos \theta \end{array} \right ) \left ( \begin{array}{c} x \\ y \end {array} \right ) $$
具体的なソースコードは下記のようになります。
#include "myJpeg.h"
#include <math.h>
#include <string.h>
#define PI 3.14159
int main(int argc, char *argv[]){
BITMAPDATA_t bitmap, rotatedBitmap;
double m, n;
int c;
int angle;
int m0, n0;
int originalm, originaln;
double rad;
char outname[256];
if(argc != 3){
printf("ファイル名と回転角度(0 - 359)を引数に指定してください\n");
return -1;
}
angle = atoi(argv[2]);
if(angle > 359 || angle < 0){
printf("ファイル名と回転角度(0 - 359)を引数に指定してください\n");
return -1;
}
/* 単位をラジアンへ変換 */
rad = (double)angle * PI / (double)180;
if(jpegFileReadDecode(&bitmap, argv[1]) == -1){
printf("jpegFileReadDecode error\n");
return -1;
}
/* 回転後画像の情報設定 */
rotatedBitmap.width = bitmap.width;
rotatedBitmap.height = bitmap.height;
rotatedBitmap.ch = bitmap.ch;
if(rotatedBitmap.width == 0 || rotatedBitmap.height == 0){
printf("回転後の幅もしくは高さが0です\n");
freeBitmapData(&bitmap);
return -1;
}
/* 回転後画像用のメモリ確保 */
rotatedBitmap.data = (unsigned char*)malloc(sizeof(unsigned char) * rotatedBitmap.width * rotatedBitmap.height * rotatedBitmap.ch);
if(rotatedBitmap.data == NULL){
printf("malloc rotatedBitmap error\n");
freeBitmapData(&bitmap);
return -1;
}
/* 事前に回転後画像の前画素を白色にしておく */
memset(rotatedBitmap.data, 0xFF, rotatedBitmap.width * rotatedBitmap.height * rotatedBitmap.ch);
/* ここから画像の回転 */
for(originaln = 0; originaln < bitmap.height; originaln++){
for(originalm = 0; originalm < bitmap.width; originalm++){
/* 回転後画像の座標を算出 */
m =
(originalm - (int)bitmap.width / 2) * cos(rad) +
(originaln - (int)bitmap.height / 2) * -sin(rad) + bitmap.width/ 2;
n =
(originalm - (int)bitmap.width / 2) * sin(rad) +
(originaln - (int)bitmap.height / 2) * cos(rad) + bitmap.height / 2;
/* 一番近い座標を四捨五入で算出 */
m0 = m + 0.5;
n0 = n + 0.5;
/* 画像外にはみ出ている場合はコピーしない */
if(m0 >= bitmap.width || m0 < 0) continue;
if(n0 >= bitmap.height || n0 < 0) continue;
/* 最近傍補間した画素の輝度値をコピー */
for(c = 0; c < rotatedBitmap.ch; c++){
rotatedBitmap.data[rotatedBitmap.ch * (m0 + n0 * rotatedBitmap.width) + c]
= bitmap.data[bitmap.ch * (originalm + originaln * bitmap.width) + c];
}
}
}
/* ここまで画像の回転 */
sprintf(outname, "%s", "rotated.jpeg");
if(jpegFileEncodeWrite(&rotatedBitmap, outname) == -1){
printf("jpegFileEncodeWrite error\n");
freeBitmapData(&bitmap);
return -1;
}
freeBitmapData(&bitmap);
return 0;
}スポンサーリンク
回転行列の逆行列を用いて回転
次は、回転行列の逆行列を用いて回転するプログラムのソースコードを紹介します。
この場合、回転後の座標に対するループの中で、下記の回転行列の逆行列を用いて回転前座標を求めながら回転処理を行うことになります。
$$ \left ( \begin{array}{c} x \\ y \end{array} \right ) = \left ( \begin{array}{cc} \cos \theta & \sin \theta \\ – \sin \theta & \cos \theta \end{array} \right ) \left ( \begin{array}{c} x’ \\ y’ \end {array} \right ) $$
具体的なソースコードは下記のようになります。
#include "myJpeg.h"
#include <math.h>
#include <string.h>
#define PI 3.14159
int main(int argc, char *argv[]){
BITMAPDATA_t bitmap, rotatedBitmap;
int m, n, c;
int angle;
int m0, n0;
double originalm, originaln;
double rad;
char outname[256];
if(argc != 3){
printf("ファイル名と回転角度(0 - 359)を引数に指定してください\n");
return -1;
}
angle = atoi(argv[2]);
if(angle > 359 || angle < 0){
printf("ファイル名と回転角度(0 - 359)を引数に指定してください\n");
return -1;
}
/* 単位をラジアンへ変換 */
rad = (double)angle * PI / (double)180;
if(jpegFileReadDecode(&bitmap, argv[1]) == -1){
printf("jpegFileReadDecode error\n");
return -1;
}
/* 回転後画像の情報設定 */
rotatedBitmap.width = bitmap.width;
rotatedBitmap.height = bitmap.height;
rotatedBitmap.ch = bitmap.ch;
if(rotatedBitmap.width == 0 || rotatedBitmap.height == 0){
printf("回転後の幅もしくは高さが0です\n");
freeBitmapData(&bitmap);
return -1;
}
/* 回転後画像用のメモリ確保 */
rotatedBitmap.data = (unsigned char*)malloc(sizeof(unsigned char) * rotatedBitmap.width * rotatedBitmap.height * rotatedBitmap.ch);
if(rotatedBitmap.data == NULL){
printf("malloc rotatedBitmap error\n");
freeBitmapData(&bitmap);
return -1;
}
/* 事前に回転後画像の前画素を白色にしておく */
memset(rotatedBitmap.data, 0xFF, rotatedBitmap.width * rotatedBitmap.height * rotatedBitmap.ch);
/* ここから画像の回転 */
for(n = 0; n < rotatedBitmap.height; n++){
for(m = 0; m < rotatedBitmap.width; m++){
/* 回転前画像の座標を算出 */
originalm =
(m - (int)rotatedBitmap.width / 2) * cos(rad) +
(n - (int)rotatedBitmap.height / 2) * sin(rad) + bitmap.width/ 2;
originaln =
- (m - (int)rotatedBitmap.width / 2) * sin(rad) +
(n - (int)rotatedBitmap.height / 2) * cos(rad) + bitmap.height / 2;
/* 一番近い座標を四捨五入で算出 */
m0 = originalm + 0.5;
n0 = originaln + 0.5;
/* 画像外にはみ出ている場合はコピーしない */
if(m0 >= bitmap.width || m0 < 0) continue;
if(n0 >= bitmap.height || n0 < 0) continue;
/* 最近傍補間した画素の輝度値をコピー */
for(c = 0; c < rotatedBitmap.ch; c++){
rotatedBitmap.data[rotatedBitmap.ch * (m + n * rotatedBitmap.width) + c]
= bitmap.data[bitmap.ch * (m0 + n0 * bitmap.width) + c];
}
}
}
/* ここまで画像の回転 */
sprintf(outname, "%s", "rotated.jpeg");
if(jpegFileEncodeWrite(&rotatedBitmap, outname) == -1){
printf("jpegFileEncodeWrite error\n");
freeBitmapData(&bitmap);
return -1;
}
freeBitmapData(&bitmap);
return 0;
}回転後画像の違い
では上記の2つのプログラムにおいて、回転実行後の画像にどのような違いがあるのかについて確認していきたいと思います。
回転行列をそのまま用いて回転した結果
まず、回転前座標に対するループの中で回転行列を利用して画像の回転を行なった結果が下図となります。

スポンサーリンク
回転行列の逆行列を用いて回転した結果
それに対し、回転後座標に対するループの中で回転行列の逆行列を利用して画像の回転を行なった結果が下図となります。

画像の違いが発生する理由
回転前座標に対するループの中で回転行列を利用して画像の回転を行なった結果の画像は、所々穴があって汚くなっているのが確認できます。
その一方で、回転後座標に対するループの中で回転行列の逆行列を利用して画像の回転を行なった結果の画像は綺麗ですね!
この2つ画像の違いは、回転行列 or その逆行列のどちらをを用いているかに起因するというよりは、回転前座標に対するループの中で回転を行うのか、回転後座標に対するループの中で回転を行うのか違いによって生じています。
回転後座標に対するループの中で回転を行う場合、回転後座標の全座標に対して回転前座標の画素をコピーしていくわけですから、当然回転後画像の全ての座標に対して画素がコピーされることになります(回転前座標が画像をはみ出る部分を除いて)。
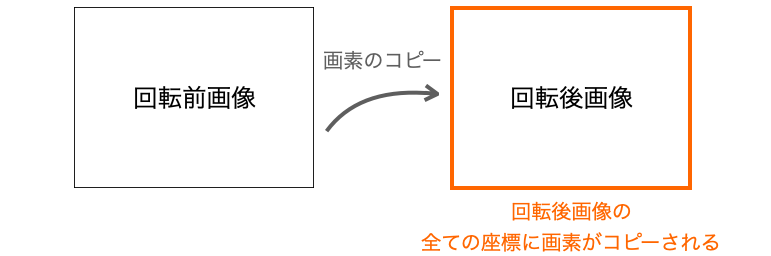
その一方で、回転前座標に対するループの中で回転を行う場合、回転前の座標の全座標が回転後座標の画素にコピーされることになります。
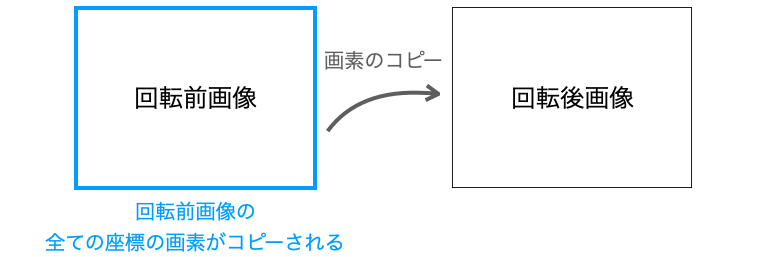
ただし、行列演算を行なって回転後座標を算出する際、回転前の座標が異なる場合でも、算出した回転後座標が同じになることがあります。
これは、画像の各画素の座標が量子化されているからです。特に今回のプログラムの場合は、画像の各座標が整数になるように量子化されています。
その一方で、行列演算を行なって求めた結果は実数となりますので、画像の座標として扱うためには整数に丸める必要があります。この丸めを行うことで、回転前の座標が異なる場合でも、算出した回転後座標が同じになることがあります。
そうなると、異なる座標の画素が、同じ座標に重複してコピーされてしまう可能性があります。ループが行われる回数は有限ですので、この重複が起こった分、回転後画像にコピーされない画素が発生することになります。
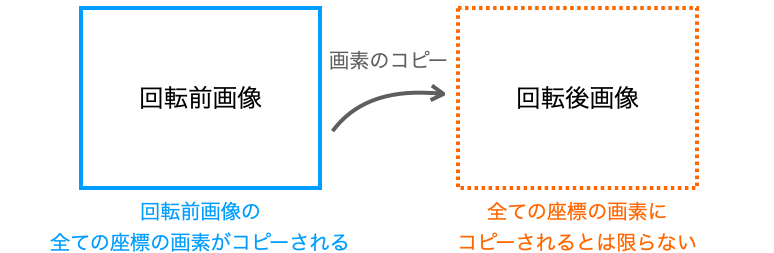
そして、そのコピーされない画素が、白色の画素として現れ、穴のように見えて画質が悪くなってしまうというわけです。
試しに 回転行列をそのまま用いて回転 を少し改造して、回転後座標のどの位置がどれくらい重複して画素値コピーされているかを可視化してみました。
黒いところほど何回も重複して画素値コピーを行われているところで、白い部分はコピーが行われなかった部分になります。余白部分は白くて当然なのですが、絵の中までコピーされていない箇所があることが確認できると思います。

こんな感じで画素のコピーが行われない箇所を防ぐためにも、画像の回転は、回転後画像の座標に対するループの中で実行する方が良いです。
画像処理における逆行列の重要性
先程の説明のように、”画像処理前” の座標に対するループの中で画像処理を行なった場合、画像処理結果の画質が悪くなる場合があります。
その一方で、”画像処理後” の座標に対するループの中で画像処理を行うことで、画像処理結果の画質の低下を防ぐことができます。
で、画像処理後の座標から画像処理前の座標を求める際には、「画像処理前の座標から画像処理後の座標を求める行列の逆行列」が必要になります。
基本的に、「画像処理前の座標から画像処理後の座標を求める行列」を考える方が直感的で分かりやすいため、行列自体は画像処理前の座標から画像処理後の座標を求めるものを考え、実際にプログラミングする際には、その「逆行列」を求めてから”画像処理プログラムの実装を行うことが多いです。
こういった理由から、画像処理においては逆行列は非常に重要です。
スポンサーリンク
まとめ
- 画像処理(特に座標変換を行う画像処理)では画像処理後の座標に対するループを用いて処理を行った方が良い
- 画像処理前の座標に対するループだと画像処理後画像に穴ができてしまい、画質が低下する可能性がある

