C言語で画像の拡大縮小（線形補間編）

SHARE

このページにはプロモーションが含まれています

このページでは、線形補間を用いた画像の拡大縮小法についての説明と、そのプログラムの例の紹介を行います。

補間とは

補間に関しては下記ページの補間とはで解説していますので、コチラを参照していただければと思います。

C言語で画像の拡大縮小（最近傍補間編）

確か存在しないデータを補うことだよね
そうだね！

この補い方に色んなアルゴリズムがあって、線形補間はそのアルゴリズムの中の１つになるよ

線形補間とは

線形補間は補間アルゴリズムの１つです。

スポンサーリンク

線形補間の考え方

線形補間とは「データとデータの間の区間は値が均等に変化するであろうと仮定して補間する」アルゴリズムになります。

最近傍補間でも出したクイズですが、例えば７日間体重を計測する必要があったのに、４日目と５日目の体重計測を忘れてしまったとしましょう。つまり、４日目と５日目のデータは存在しないことになります。

他の日の体重計測結果が下記のような時、? で表した４日目と５日目の体重はいくつだったと考えられるでしょう？

50.5, 51.5, 51.0, ?, ?, 52.5, 52.0

ここで３日目の体重 51.0 と ６日目の体重 52.5 に注目してみます。３日間で体重が 1.5 増えたことになります。

線形補間では、この区間（つまり３日間）で体重が均等に変化したと考えます。

つまり、３日間で 1.5 増えたのですから、１日で 0.5 増えたと仮定して補間を行います。

つまり、線形補間では、４日目の体重は 51.0 + 0.5 = 51.5、５日目の体重は 51.0 + 0.5 * 2 = 52.0 と補間されます。

この体重の例だと４日目は 51.5、５日目は 52.0 以外考えられなかったなぁ

そうだね！

おそらく多くの人がその値を補間したんじゃないかな

それくらい人間にとって自然な考え方＆単純な補間方法なんだ

線形補間を行う計算式

最近傍補間では四捨五入だけ行えばよかったので簡単でしたが、この線形補間を行うには若干複雑な計算を行う必要があります。

次はこの線形補間を行う際の計算式について説明します。

で、これはグラフで考えるとすごく分かりやすいです。

例えば先程の体重の日毎の計算結果をグラフで表すと下図のようになります。

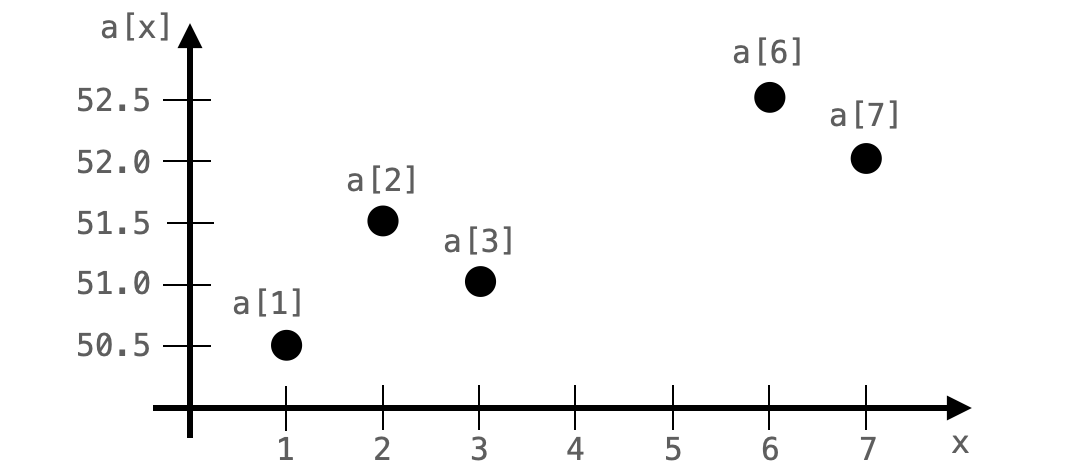
体重の変化をグラフで表した様子

横軸 x は日を表し、縦軸 a[x] は x 日目の体重を表します。プログラミング的に考えると a は配列のように考えて良いです。

そして、線形補間は「データとデータの間の区間は値が均等に変化するであろうと仮定して補間する」です。

つまりこれは、線形補間で補間する値は点と点の間を結んだ直線上の値になることを表します。

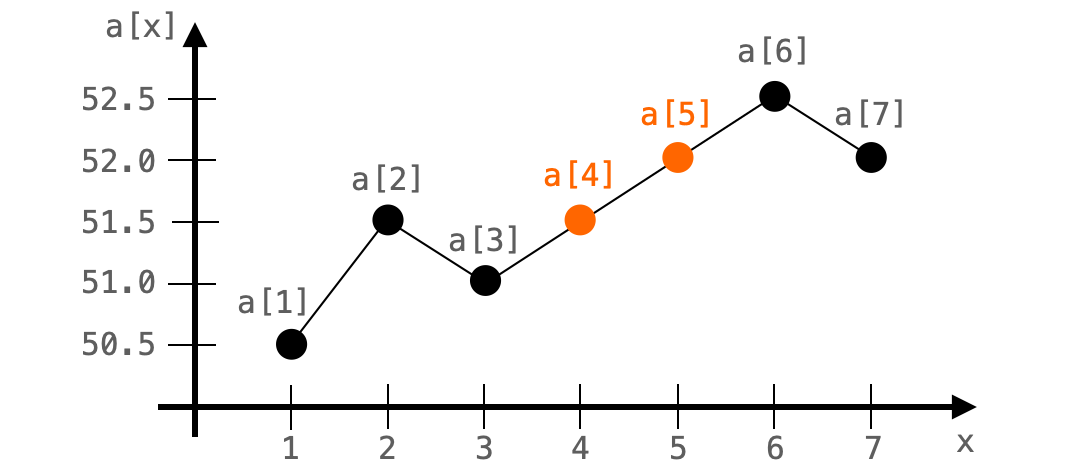
グラフを直線で結んだ様子

なので、要は線形補間で補う値は、直線上の値を計算するで求めることができます。

では、ここまでの考え方を踏まえて、線形補間で補間する値の求め方について解説していきたいと思います。一旦体重の例は置いておきます。

x0 と x1 の２点間にある x' の値 a['x] がどのように計算できるかについて考えてみましょう。

この時の各変数の値の関係を図で表すと下図のようになります。

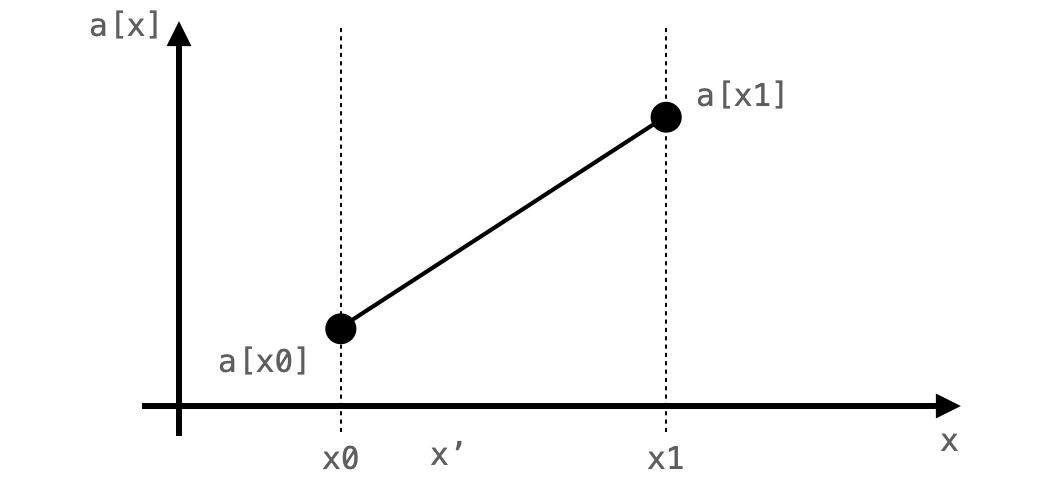
２点間を直線で結んだ様子

で、線形補間では a['x] は下図のように a[x0] と a[x1] を結んだ直線上に存在すると仮定して値を求めることになります。

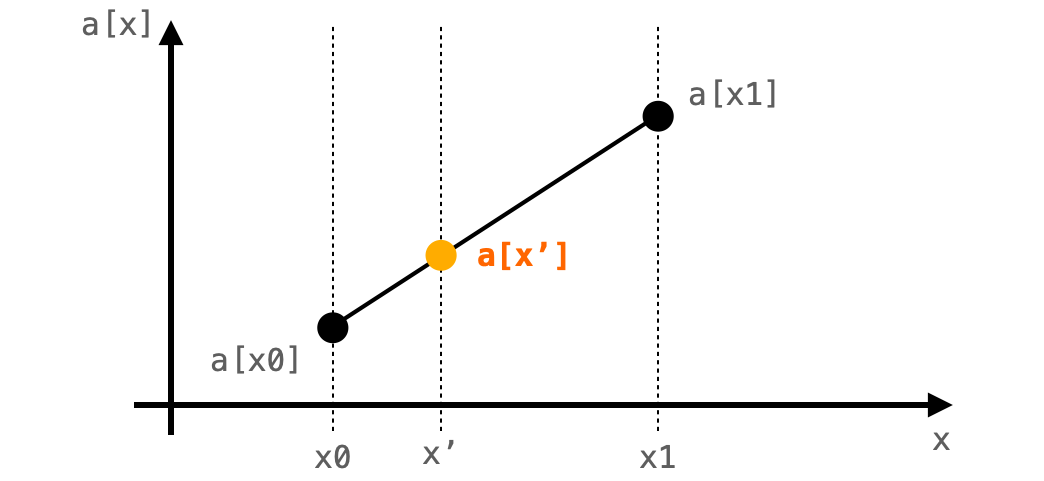
線形補間で直線上にデータを補う様子

この仮定を行うと、a['x] の値は下記の式で求めることができます。

１次元の線形補間で求める値の計算式 
a['x] = a[x0] + (x' - x0) * (a[x1] - a[x0]) / (x1 - x0)

(a[x1] - a[x0]) / (x1 - x0) は直線の傾きになります。

これはつまり、１単位あたりの変化量になります。これは、x が 1 増えると値が (a[x1] - a[x0]) / (x1 - x0) 変化することを意味します。

さらに、この傾きに x の変化量 (x' - x0) を掛けると a[x0] から値がどれだけ変化するかを求めることができます。

ですので、この a[x0] に対してその a[x0] からの値の変化量を足してやれば、a['x] の値を求めることができることになります。

思ったより難しいね…

画像の拡大縮小時に限って考えると、もうちょっとだけ簡略化できるよ

それについては後述で説明するよ！

線形補間による画像の拡大縮小

ではここまで解説してきた線形補間を用いて画像の拡大縮小を行う方法について解説していきます。

画像の拡大縮小を行う際には、線形補間を縦方向と横方向の２次元的に考える必要があります。この２次元的に考えて線形補間する方法を「双線形補間」や「バイリニア補間」と呼んだりします（このページでは単に線形補間と呼びます）。

スポンサーリンク

画像の拡大縮小

画像の拡大縮小の基本的な考え方は下記ページで解説していますので、まだ読んでいない方は是非読んでみてください。ここからの解説がより理解しやすくなると思います。

画像の拡大縮小・リサイズの原理、アルゴリズムによる違いを解説！

↑ のページに記載の通り、横方向に H 倍、縦方向に V 倍拡大縮小する場合、拡大縮小後画像の座標（X, Y）と元画像の座標（x, y）の関係は下記式で表すことができます。

拡大縮小前後の座標の関係 
x = 1 / H * X
y = 1 / V * Y

これはつまり、全座標 (X, Y) の画素に上式で求まる元画像の座標 (x, y) の画素をコピーしてやれば、拡大縮小後の画像を作成することができることになります。

ただし、上式の計算で求められる座標（x, y）の画素が元画像に存在しない場合があります。これは具体的には x や y が整数でない場合です。

つまり、画像の拡大縮小では、存在しない画素をコピーする必要があるということです。

その存在しないデータを補間で補ってコピーするんだよね！
そうそう！

そして、このページではその補間を線形補間で行って行くよ

存在しない画素をコピーする場合、元画像の座標 (x, y) の存在しない画素を推測し、その推測値で補って拡大縮小処理を行います。この補う処理が補間処理です。

このページでは、この補間処理を前述で解説した「線形傍補間」により行います。

画像の拡大縮小においては、補う画素の輝度値を周囲の４つの画素の間の輝度値は均等に変化するであろうと仮定して補間を行います。

画像拡大縮小時の線形補間

ではその画像拡大縮小時に行う線形補間をどのようにして行うかについて説明していきたいと思います。

下図のような座標 (x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) の画素の間に存在する座標 (x', y') の画素を線形補間で求めることを考えていきたいと思います。

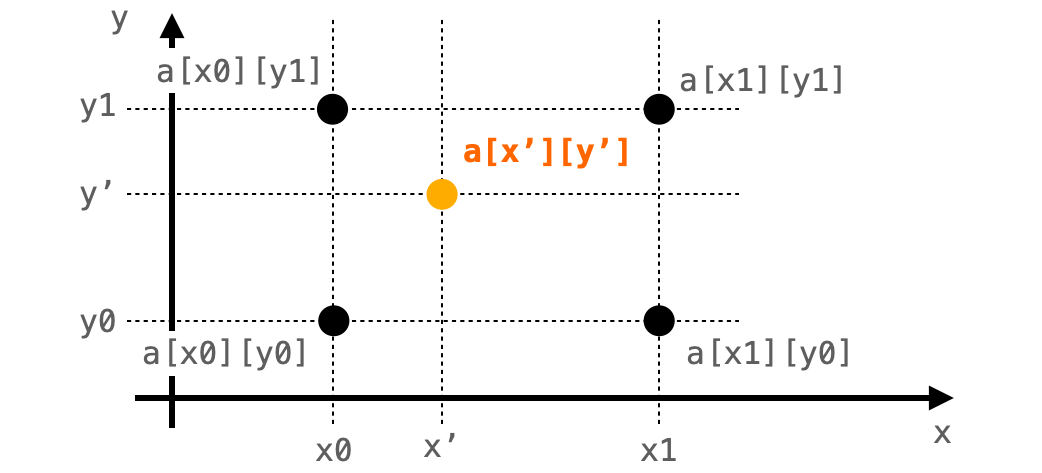
補間する画素と周囲４画素の関係

a[x][y] には、座標 (x, y) の画素が格納されており、下記の４つの画素から a[x][y] を補間することになります。

  • a[x0][y0]：座標 (x0, y0) の画素
  • a[x0][y1]：座標 (x0, y1) の画素
  • a[x1][y0]：座標 (x1, y0) の画素
  • a[x1][y1]：座標 (x1, y1) の画素

本当は画素というよりも、画素の色ごとの輝度値という方が正しいのですが、この節では簡単のため単に「画素」と呼びます

実際にはこの節で紹介する補間式は各色の輝度値に対して計算する必要があります

後で紹介する実際のプログラムでは各色の輝度値も考慮したものになっています

[/codebox]

さらに座標 (x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) は座標 (x', y') の周囲の４つの画素の座標になりますので、下記により求めることができます。

  • x0：x' の小数点以下を切り捨て
  • x1：x0 + 1
  • y0：y' の小数点以下を切り捨て
  • y1：y0 + 1

線形補間ではこの４つの画素の色が均等に変化すると仮定して補間を行います。

４つの画素の間の色が均等に変化するってイメージしにくいなぁ…
そうだね！なので、もっと簡単に考えられる方法を考えていこう！

といっても、４つの画素をいきなり考慮するのは大変です。なので、２つの画素に注目しながら考えていくことにします。

ここで下の図のように座標 (x0, y') と座標 (x1, y') を追加し、これらの画素（つまり a[x0][y'] と a[x1][y']）について考えてみましょう！

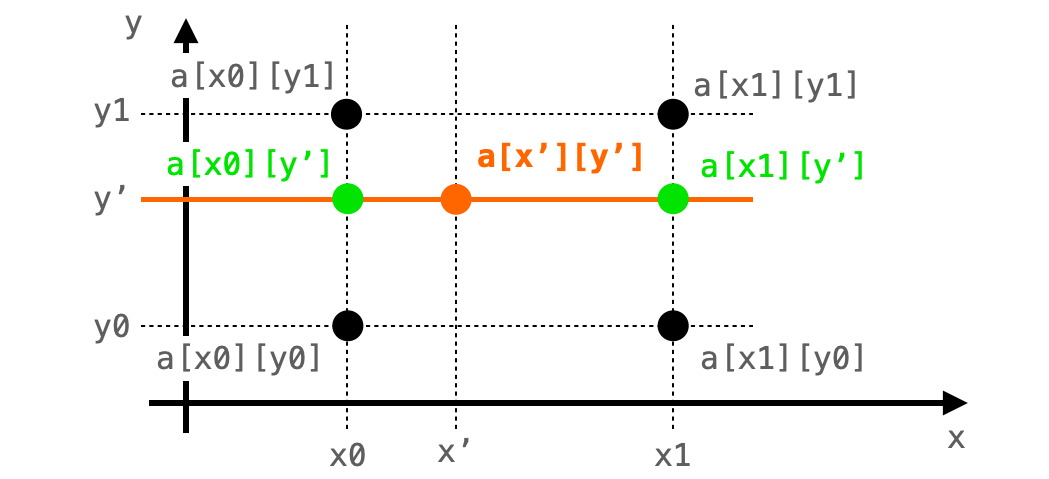
３つの画素が同じy上に存在する様子

座標 (x', y') と座標 (x0, y') と座標 (x1, y') は全て y = y' の直線上に存在します。つまりこれらの３点間で変化するのは x の１方向のみです。

なので、座標 (x', y') の画素 a[x'][y'] は座標 (x0, y') と座標 (x1, y') の画素 a[x0][y'] と a[x1][y'] から単なる線形補間（x 方向の１方向のみを考慮した線形補間）により求めることができます。

計算式は下記のようになります。

座標 (x',y') の画素を求める計算式 
a[x'][y'] = a[x0][y'] + (x' - x0) * (a[x1][y'] - a[x0][y']) / (x1 - x0)

線形補間を行う計算式で紹介した式に比べると、配列の添字が２つになっていますが単に [y'] が追加されているだけで計算式のベースは変わっていないことが確認できると思います。

ここまでの理屈は分かった！

だけどこの計算を行うためには a[x0][y'] と a[x1][y'] を求めておく必要があるよね？

その通り！

この２つについても線形補間で求められるよ！

先程紹介した式では a[x0][y'] と a[x1][y'] を使用していますが、これらも画像上の画素として存在しない可能性がありますので補間をしてやる必要があります。

これらも１方向に対する線形補間で求めることができます。

座標 (x0, y') の画素は座標 (x0, y0) と座標 (x0, y1) は x = x0 の直線上、座標 (x1, y') の画素は座標 (x1, y0) と座標 (x1, y1) は x = x1 の直線上にそれぞれ存在します。

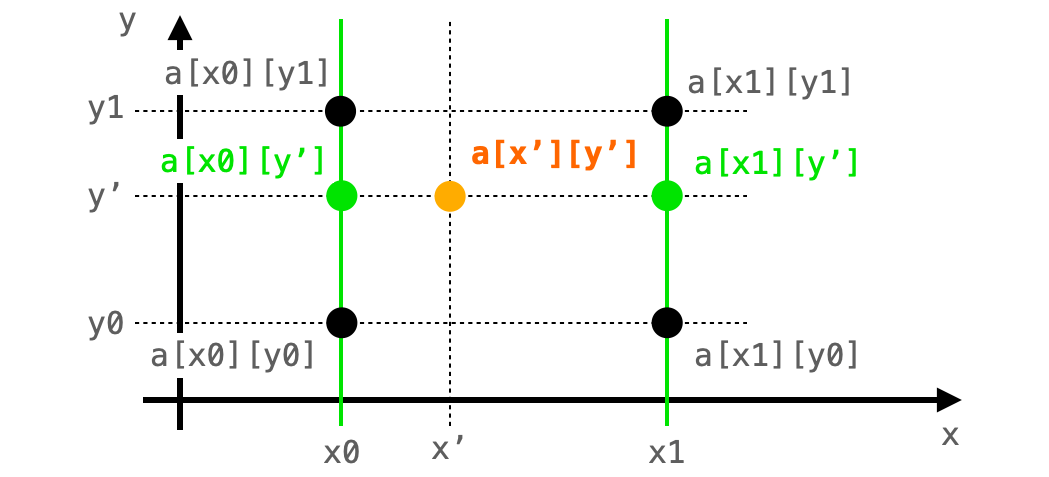
３つの画素が同じx上に存在する様子

ですので、a[x0][y'] と a[x1][y'] に関しては y 方向１方向のみに対する線形補間で求めることができます。

それぞれを求める時の式は下記のようになります。

座標 (x0,y') の画素の画素を求める計算式 
a[x0][y'] = a[x0][y0] + (y' - y0) * (a[x0][y1] - a[x0][y0]) / (y1 - y0)
座標 (x1,y') の画素を求める計算式 
a[x1] [y']= a[x1] [y0] + (y' - y0) * (a[x1] [y1] - a[x1] [y0]) / (y1 - y0)

a[y']['x]  を求める式の a[x0][y'] と a[x1][y'] にそれぞれの右辺を代入し、式を整理すると下記のようになります。

これが「画像拡大縮小時に画素を線形補間で求める式」になります。

座標 (x',y') の画素を求める計算式 
a[x'][y'] = 
    a[x0][y0] * (1 - dx) * (1 - dy) +
    a[x0][y1] * (1 - dx ) * dy +
    a[x1][y0] * dx * (1 - sy) +
    a[x0][y1] * dx * dy

実際には画素は RGB 等の複数の色の輝度値から構成されますので、上記の式で色ごとに線形補間を行う必要があります。

ここで dx と dy はそれぞれ下記式から求められる値としています。

dxとdyを求める式 
dx = (x’ - x0) / (x1 - x0)
dy = (y' - y0) / (y1 - y0)

さらに座標 (x’, y’) は座標 (x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) の間に存在するわけですので、x0 と x1、y0 と y1 の差は 1 になります。

つまり、dx と dy は下記で求めることができることになります。

dxとdyを求める式 
dx = (x’ - x0)
dy = (y' - y0)

線形補間を用いた画像の拡大縮小の処理の流れ

ここまでの解説のまとめとして、線形補間を用いた画像の拡大縮小の処理の流れを解説しておきます。

線形補間を用いた画像の拡大縮小は、拡大縮小後画像の全座標 (X, Y) に対して下記を行うことで実現することができます。

拡大縮小前画像の座標を求める

まずは下記式で拡大縮小後画像の座標  (X, Y) に対応する拡大縮小前画像における座標 (x', y') を求めます

拡大縮小前後の座標の関係 
x' = 1 / H * X
y' = 1 / V * Y

周囲４点の座標を求める

続いて下記により座標 (x', y') の周囲４点の座標 (x0, y0)、(x0, y1)、(x1, y0)、(x1, y1) を求めます。

  • x0：x' の小数点以下を切り捨て
  • x1：x0 + 1
  • y0：y' の小数点以下を切り捨て
  • y1：y0 + 1

周囲４点の画素から線形補間を行う

さらに、下記の式により周囲４点の画素から線形補間を行い、座標 (x', y') の画素を求めます。

実際には画素は RGB 等の複数の色の輝度値から構成されますので、下記の式で色ごとに線形補間を行う必要があります。

座標 (x',y') の画素を求める計算式 
a[x'][y'] = 
    a[x0][y0] * (1 - dx) * (1 - dy) +
    a[x0][y1] * (1 - dx ) * dy +
    a[x1][y0] * dx * (1 - sy) +
    a[x0][y1] * dx * dy

ここで dx と dy はそれぞれ下記式から求められる値としています。

dxとdyを求める式 
dx = (x’ - x0)
dy = (y' - y0)

この求めた a[x][y] が拡大縮小後画像の座標 (X, Y) の画素になります。

つまり、この a[x][y] を拡大縮小後画像の画素を格納する配列などにコピーすることで、１画素分の処理が完了したことになります。

スポンサーリンク

線形補間による画像の拡大縮小プログラム

ではここまで解説してきた「線形補間による画像の拡大縮小」をC言語でプログラミングするとどのようになるかについて解説していきたいと思います。

ソースコード

線形補間を用いて画像の拡大縮小を行うプログラムのソースコード例は下記のようになります。

main.c 
#include "myJpeg.h"

int main(int argc, char *argv[]){

  BITMAPDATA_t bitmap, scaledBitmap;
  int m, n, c;
  int m0, m1, n0, n1;
  double originalm, originaln;
  double dm, dn;
  double scaleW, scaleH;
  char outname[256];

  if(argc != 4){
    printf("ファイル名、幅方向拡大率、高さ方向拡大率の３つを引数に指定してください\n");
    return -1;
  }

  scaleW = atof(argv[2]);
  scaleH = atof(argv[3]);

  if(jpegFileReadDecode(&bitmap, argv[1]) == -1){
    printf("jpegFileReadDecode error\n");
    return -1;
  }

  /* 拡大後の画像の準備 */
  scaledBitmap.width = scaleW * bitmap.width;
  scaledBitmap.height = scaleH * bitmap.height;
  scaledBitmap.ch = bitmap.ch;

  if(scaledBitmap.width == 0 || scaledBitmap.height == 0){
    printf("拡大縮小後の幅もしくは高さが０です\n");
    freeBitmapData(&bitmap);
    return -1;
  }

  scaledBitmap.data = (unsigned char*)malloc(sizeof(unsigned char) * scaledBitmap.width * scaledBitmap.height * scaledBitmap.ch);
  if(scaledBitmap.data == NULL){
    printf("malloc scaledBitmap error\n");
    freeBitmapData(&bitmap);
    return -1;
  }

  /* ここから線形補間による拡大縮小 */
  for(n = 0; n < scaledBitmap.height; n++){
    for(m = 0; m < scaledBitmap.width; m++){
      for(c = 0; c < scaledBitmap.ch; c++){

        /* 拡大前画像における座標計算 */
        originalm = (double)m / (double)scaleW;
        originaln = (double)n / (double)scaleH;

       /* 周囲４点の座標を計算 */
        m0 = (int)originalm;
        m1 = m0 + 1;
        n0 = (int)originaln;
        n1 = n0 + 1;

        /* m1やn1が画像をはみ出た場合の処理 */
        if(m1 == bitmap.width) m1 = bitmap.width - 1;
        if(n1 == bitmap.height) n1 = bitmap.height - 1;

        /* 元々の座標とm0,n0との距離を計算 */
        dm = originalm - m0;
        dn = originaln - n0;

        /* 周囲４点の画素の色cの輝度値より線形補間 */
        scaledBitmap.data[scaledBitmap.ch * (m + n * scaledBitmap.width) + c]
          = bitmap.data[bitmap.ch * (m1 + n1 * bitmap.width) + c] * dm * dn
          + bitmap.data[bitmap.ch * (m1 + n0 * bitmap.width) + c] * dm * (1 - dn)
          + bitmap.data[bitmap.ch * (m0 + n1 * bitmap.width) + c] * (1- dm) * dn
          + bitmap.data[bitmap.ch * (m0 + n0 * bitmap.width) + c] * (1 -dm) * (1 - dn);
      }
    }
  }
  /* ここまで線形補間による拡大縮小 */

  sprintf(outname, "%s", "linear.jpeg");

  if(jpegFileEncodeWrite(&scaledBitmap, outname) == -1){
    printf("jpegFileEncodeWrite error\n");
    freeBitmapData(&bitmap);
    return -1;
  }

  freeBitmapData(&bitmap);

  return 0;
}

ここまで解説を読んでくださった方であれば、変数名を下記のように対応づけて読むと分かりやすいかと思います。

  • m, n：X, Y
  • originalm, originaln：x’, y’ (x, y)
  • m0, n0,  m1, n1：x0, y0, x1, y1
  • scaleW, scaleH：H, V

コンパイルと実行

このソースコードをコンパイルする方法や実行の方法は、下記ページで紹介している最近傍補間のものと同じですので、下記ページを参考にしていただければと思います。

C言語で画像の拡大縮小（最近傍補間編）

ただし、出力されるファイル名がこのページで紹介している線形補間のプログラムの場合は linear.jpeg になるので注意してください。

スポンサーリンク

プログラムの説明

続いてプログラムの説明を行っていきたいと思います。

拡大縮小以外の処理は下記ページの最近傍補間のプログラムと同じですので、下記ページを参考にしていただければと思います。

C言語で画像の拡大縮小（最近傍補間編）

このページでは最近傍補間のプログラムと異なる「拡大縮小処理」についてのみ解説させていただきます。

拡大縮小処理

では拡大縮小処理の説明を行っていきます。

拡大縮小処理は、拡大縮小後の全画素＆全色に対して補間処理を行なっていきますので、下記のループで繰り返し処理を行います。

全画素＆全色に対するループ 
  for(n = 0; n < scaledBitmap.height; n++){
    for(m = 0; m < scaledBitmap.width; m++){
      for(c = 0; c < scaledBitmap.ch; c++){

下記では拡大縮小後の座標（m, n）が、元画像（拡大縮小前の画像）ではどの座標 (originalm, originaln) にあたるかを計算しています。

拡大前画像の座標の計算 
        /* 拡大前画像における座標計算 */
        originalm = (double)m / (double)scaleW;
        originaln = (double)n / (double)scaleH;

originalm と originaln は純粋に拡大縮小率と拡大後画像の座標 (m, n) から計算した元画像上の座標になります。

さらに下記により、座標 (originalm, originaln) の周囲４つの座標を求めています。

周囲４つの座標の計算 
       /* 周囲４点の座標を計算 */
        m0 = (int)originalm;
        m1 = m0 + 1;
        n0 = (int)originaln;
        n1 = n0 + 1;

        /* m1やn1が画像をはみ出た場合の処理 */
        if(m1 == bitmap.width) m1 = bitmap.width - 1;
        if(n1 == bitmap.height) n1 = bitmap.height - 1;

m1 と n1 は画像外の座標になる可能性があるので、その場合は画像の内側の座標になるように最後の２文で調整しています。

さらに下記で、originalm と m0、originaln と n0 のそれぞれの距離を計算しています。

距離の計算 
        /* 元々の座標とm0,n0との距離を計算 */
        dm = originalm - m0;
        dn = originaln - n0;

以上により、座標 (originalm, originaln) の画素（の輝度値）を線形補間で求める準備が整ったことになります。

最後に下記により、線形補間を用いて座標 (originalm, originaln) の画素の輝度値を求め、それを拡大縮小後の画像データを指す scaledBitmap.data にコピーしています。

線形補間した画素の輝度値をコピー 
        /* 周囲４点の画素の色cの輝度値より線形補間 */
        scaledBitmap.data[scaledBitmap.ch * (m + n * scaledBitmap.width) + c]
          = bitmap.data[bitmap.ch * (m1 + n1 * bitmap.width) + c] * dm * dn
          + bitmap.data[bitmap.ch * (m1 + n0 * bitmap.width) + c] * dm * (1 - dn)
          + bitmap.data[bitmap.ch * (m0 + n1 * bitmap.width) + c] * (1- dm) * dn
          + bitmap.data[bitmap.ch * (m0 + n0 * bitmap.width) + c] * (1 -dm) * (1 - dn);
      }

c に対するループの中で上記を実行するため、各色の輝度値がコピーされる、つまり画素がコピーされることになります。

あとはこれを拡大縮小後の全画素に対して実行すれば良いだけです。

ちょっとここで注意が必要なのは画像データを２次元データではなく１次元データとして扱っているところです。

１次元データとして扱うために上記のように添字部分の計算がちょっと複雑になっています。

２次元データを１次元データとして扱う方法は下記ページの１次元データで解説していますので詳しく知りたい方は是非読んでみてください！

二次元データの扱い方を解説するページのアイキャッチ C言語で２次元データをいろいろな方法で扱ってみる（二次元配列・ポインタのポインタなど）

画像処理前後の画像

最後に紹介したプログラムを実行することでどのような結果が得られるのかを紹介しておきます。

プログラム実行時の第１引数に指定する JPEG ファイルは下図のようなものにしたいと思います。

さらに、横方向の拡大縮小率を 0.5、縦方向の拡大縮小率を 0.7 として引数に指定した場合、下図のように拡大縮小後の画像が得られます。

まとめ

このページでは、線形補間による画像の拡大縮小について解説し、そのプログラムの紹介を行いました！

線形補間では、「ある画素とある画素の間の輝度値は均等に変化しているだろう」と仮定して補間を行います。

おそらく一番使われている補間アルゴリズムだと思います。特に写真などのような画像においては、この線形補間で十分綺麗に拡大縮小を行うこともできます。

プログラミングを行なっていく上で必ず役に立つと思いますので、是非線形補間の考え方や計算方法、プログラムの書き方などを覚えていっていただければと思います。

最も簡単な補間アルゴリズムである最近傍補間（ニアレストネイバー補間）については下のページで紹介していますので、興味があれば読んでみてください。

C言語で画像の拡大縮小（最近傍補間編）

同じカテゴリのページ一覧を表示

前の記事

C言語で画像の拡大縮小（最近傍補間編）

次の記事

【C言語】画像をグレースケール化
画像のグレースケール化の解説ページアイキャッチ