このページでは、C言語で「底を指定して対数を求める方法」について解説していきます。
これにより、”1 以外の任意の正数” を底とした対数を求めることができるようになります。
この底を指定して対数を求める際には、下記の関数を利用します。
log関数：底をeとするxの対数を求める関数eはネイピア数
log2関数：底を2とするxの対数を求める関数log10関数：底を10とするxの対数を求める関数
これらの関数については下記ページで解説していますので、使い方をご存知ない方は事前に下記ページを読んでいただくことをオススメします。
【C言語】log・log2・log10 関数で対数を求める
底を指定して対数を求める方法
前述紹介した log 関数・log2 関数・log10 関数を実行して求められるのは下記を底とする対数のみとなります。
e（ネイピア数）210
ただ、これらの値を底とする対数さえ求められれば、「底の変換」を利用することで他の値を底とする対数も求めることが可能です。
底の変換を利用する
底の変換とは、下記の等式が成立することを利用することで底を変換することを言います。
$$ \log_b x = \frac{ \log_a x }{ \log_a b } $$
上式は、右辺の底を \( a \) とする対数同士の除算を行うことで、底を \( b \) とする対数の計算結果が得られることを示しています。
こんな感じで、”同じ値を底とする対数同士の除算” を行うことにより、”他の値を底とする対数” を求めることができます。
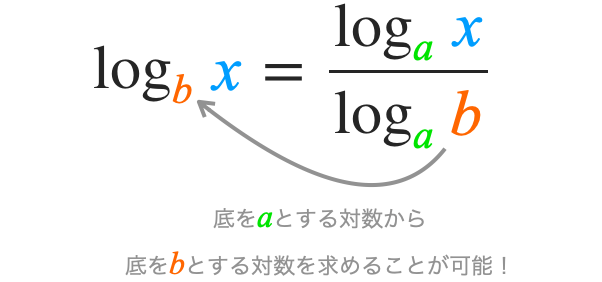
上式における \( a \) は何でも良いので、つまりは “何かしらの値” を底とする対数さえ求められれば、他の任意の値を底とする対数を求めることができることになります。
スポンサーリンク
C言語で底の変換を行う方法
前述の “何かしらの値” とは、対数を求めることさえできれば何でも良いです。
なので、底が e でも 2 でも 10 でも対数を求めることさえできれば良いです。
つまり、下記の関数を利用すれば、底の変換を行うことが可能ということになります。
log関数：底をeとするxの対数を求める関数log2関数：底を2とするxの対数を求める関数log10関数：底を10とするxの対数を求める関数
より具体的には、下記のいずれかを実行することで、x に対する底を b とする対数を求めることができます（求めた対数は p に格納されます）。
p = log(x) / log(b);p = log2(x) / log2(b);p = log10(x) / log10(b);上記は理論的には全て同じ結果になります（誤差が発生する可能性はあるかも…）。
上記の処理は x に対する底を b とする対数を求めるものであり、つまりは下記式の結果を算出することになります。
$$ \log_b x $$
分母側で実行する関数の引数によって底を指定することができますので、 つまりは上記の処理によって底 b を指定して対数を求めることができることになります。
底に指定できるのは 1 以外の正数のみ
ただし、底 b に指定できるのは 1 以外の正数のみになります（つまり b に指定できるのは b > 0 かつ b ≠ 1 を満たす正の実数）。
下記式を見ていただければ分かる通り、b が 1 の場合は右辺の分母が 0 になってしまいます。
$$ \log_b x = \frac{ \log_a x }{ \log_a b } $$
さらに、\( \log_a b \) を計算することは下記を満たす p を求めることと同義です。
$$ b = a ^ p $$
b が 0 以下である場合、上式は実数の世界では成立しない or 無限大の値となります。
なので、底 b に指定できるのは 1 以外の正数のみにとなります。
ただ、これは今回紹介した対数の計算方法に問題があるわけではなく、Wikipedia においても下記のように定義されており、「底 b に指定できるのは 1 以外の正数のみ」は一般的な制限と考えて良いと思います。
実数の対数 logb x は、底 b が 1 でない正数であり (b ≠ 1, b > 0)、真数 x が正数である場合 (x > 0) について定義される。
引用元：Wikipedia
底を指定して対数を求める関数
ここまで解説してきた内容に基づいて、次は「底を指定して対数を求める関数」を紹介していきたいと思います。
スポンサーリンク
logN 関数
その関数が下記の logN となります。下記関数を利用するためには math.h をインクルードしておく必要があるので注意してください。
#include <math.h>
double logN(double x, double b) {
return log(x) / log(b);
}logN は「底を b とする x の対数」を返却する関数になります。
log 関数を利用して底の変換を行なうことで、1 以外の正数を求めることを実現しています。log 関数の部分は log2 関数や log10 関数に置き換えても同様の結果が得られるはずです（誤差による差は出るかも）。
logN 関数の実行例
例えば下記のように logN 関数を実行すれば、底に 7 を指定した対数を求めることができます。
double b = 7;
for (int i = 0; i < 5; i++) {
double x = pow(b, i);
printf("%f : %f\n", x, logN(x, b));
}実行結果は下記のようになり、右側の値が左側の値に対する底を 7 とする対数となっていることが確認できると思います。
7.000000 : 1.000000 49.000000 : 2.000000 343.000000 : 3.000000 2401.000000 : 4.000000
ちなみに上記コードで利用している pow は冪乗を求める関数です。詳しくは下記ページで解説していますので、詳しく知りたい方はこちらをご参照ください。
【C言語】べき乗計算・累乗計算を行う方法（pow関数）
また、下記のように logN 関数を実行することで、logN 関数と log10 関数の結果を比較することができます。
for (int x = 1; x <= 10; x++) {
double a = logN(x, 10);
double b = log10(x);
printf("%f : %f\n", a, b);
}実行結果は下記のようになり、同じ出力結果が得られることが確認できると思います。
0.000000 : 0.000000 0.301030 : 0.301030 0.477121 : 0.477121 0.602060 : 0.602060 0.698970 : 0.698970 0.778151 : 0.778151 0.845098 : 0.845098 0.903090 : 0.903090 0.954243 : 0.954243 1.000000 : 1.000000
ただ、出力結果は同じですが実際には logN 関数（b に 10 を指定）と log10 関数とでは誤差によって若干の差が生じます。
これは、下記ページで紹介している手順で “表示する小数点以下の桁数” を増やすことで確認できます。
【C言語】printfで小数点以下の桁をたくさん表示する方法
この誤差は、logN 関数で使用している log 関数を logl関数に置き換えることで抑えることは可能です（ただ、誤差は抑えることはできるものの log10 関数とは全く同じにはなりませんでした…）。
まとめ
このページでは、C言語で「底を指定して対数を求める方法」について解説しました！
C言語には “底を指定して対数を求める標準ライブラリ関数” は用意されていませんが、底の変換を利用することで log 関数・log2 関数・log10 関数等から任意の 1 以外の正数を底とする対数を求めることが可能です。
このページを読んで久しぶりに底の変換という言葉や底の変換式を見て「懐かしい！」と感じた方も多いのではないでしょうか？
こんな感じで昔学校で学んだことがプログラミングで活かせることは多いです。数学が苦手だった方もプログラミングと絡めて学べば理解しやすいと思いますので、苦手意識を持たずに色んなプログラミングに挑戦していきましょう！
